物光与参考光强度比对数字全息再现像质的影响
2014-06-23宋修法于梦杰王华英刘佐强高亚飞刘飞飞
宋修法,于梦杰,王华英,,刘佐强,高亚飞,刘飞飞
(1.河北工程大学理学院,邯郸056038;2.河北工程大学信息与电气工程学院,邯郸056038)
物光与参考光强度比对数字全息再现像质的影响
宋修法1,于梦杰2,王华英1,2,刘佐强2,高亚飞2,刘飞飞2
(1.河北工程大学理学院,邯郸056038;2.河北工程大学信息与电气工程学院,邯郸056038)
为了提高数字全息显微中的重建精度及速率,采用理论分析与实验验证相结合的方法,对数字全息显微中基于同态信号处理的广义线性重建算法进行了理论分析,比较了同一物场在不同物光与参考光强比条件下的实验结果。结果表明,随着参考光与物光光强比的不断增大,广义线性重建算法再现像质得到明显改善,但当这一比值增大到一定值时,再现像质量则逐渐下降。寻找合适的物光、参考光光强比,是利用数字全息广义线性重建算法实现高质量再现像的重要条件。
全息;线性重建;参考光强度;同态信号处理
引 言
数字全息技术是一种新型的全息成像与测量技术,它利用光电耦合器件CCD记录全息图,利用计算机技术对光学衍射过程进行数值模拟再现物光波前,得到定量的强度和位相信息,实现了对全息记录、存储、传输、滤波、多视角显示等过程中的数字化处理。数字全息技术的独特优势使其成为光学前沿领域的研究热点,有着广阔的应用前景[1-5],但它仍存在一些不足,如再现算法的实时性差、重建精度还有待提高等。因此,如何提高数字全息的重建精度、速度仍是目前急需解决的热点问题。
数字全息重建的理论依据是标量衍射理论。目前常用的重建算法主要有卷积重建法、角谱重建法和菲涅耳变换重建法,它们都是基于傅里叶变换的,在重建过程中都采用了线性快速傅里叶变换,所以3种算法被称为基于快速傅里叶变换的线性重建算法。其中,菲涅耳变换法和角谱算法用得较多,尤其是角谱算法,不仅可以方便地用于频域滤波,同时又没有最小重建距离的限制[6]。然而该类重建方法在全息图的“实时”重建中,要在频域滤除不需要的0级及-1级衍射谱,而这个过程需要通过手工选取滤波区域实现,不可能真正实现再现的实时。同时,在频域滤波过程中还容易导致物体频谱中部高频成分的丢失及0级滤除得不彻底,而造成再现像分辨率的降低及重建误差。如PARK等人提出了散斑数字全息显微术方法[7],但需要记录大量全息图,实时性较差。PAN等人利用相干衍射成像中的迭代算法[8]进行全息重建,滤除了0级谱的干扰,提高了重建精度,但重建速度仍未得到全面提高。PAVILLON等人在迭代重建算法的基础上提出了非线性滤除0级谱的方法[9],实现了数字全息重建的高精度及实时性,但该方法只说明了记录全息图时要保证参考光光强要远远大于物光光强,并未给出具体的记录条件。
针对这一问题,首先通过对基于同态信号处理的广义线性重建算法进行了理论分析[10],对广义线性重建算法的记录条件进行了优化,通过实验研究,分析对比了不同物光与参考光光强比值下广义线性重建算法再现像质量的优异。
1 数字全息理论基础分析
平面参考光预放大数字全息[11-12]的记录系统坐标示意图如图1所示,其中xo-yo,xφ-yφ,x-y,xi-yi依次表示为物平面、透镜(microscope object,MO)平面、全息图平面及像平面。MO的焦距用f表示,do,dφ,d依次为MO的物距、MO平面与CCD平面的距离、全息图的记录距离,其中MO的像距用di表示,且满足d=d+d,iφ
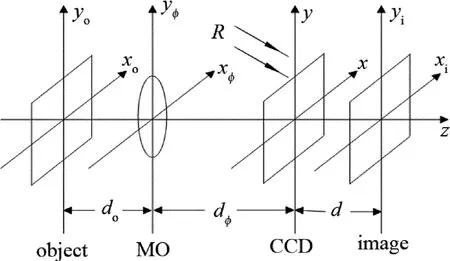
Fig.1 Coordinate schematic of pre-magnification digital holography recorded with plane reference
假设在CCD平面记录的物光波、参考光波的复振幅分布分别为O(x,y)和R(x,y),其中参考光波的表达式为:

式中,R0表示参考光波的振幅分布,fx,fy表示平面参考光在x,y方向的空间频率。CCD记录平面的光波干涉场强度分布为:

式中,*表示复共轭运算。
为了获得全息图的频谱分布,对(2)式两边作傅里叶变换。在全息图的频谱分布中,由于自卷积的作用0级谱的频谱带宽分布的范围较大,为±1级谱带宽分布的两倍,占据了大量的频谱资源,使原始像的亮度比较暗淡,对细节信息的分辨造成了影响,降低了再现像质量。为了有效地抑制0级谱对再现像的干扰,在全息图的记录过程中,一般采用离轴全息记录光路,使0级谱与±1级谱实现完全分离,但这种方法并未提高全息记录系统的成像分辨率,对此,许多研究学者提出了滤除0级谱及-1级谱[13-15]的再现方法,虽然在一定程度上抑制了0级谱及-1级谱的干扰,但仍然存在再现实时性差等问题。
2 广义线性重建算法理论分析
数字全息图的重建是数字全息显微中的一个重要步骤,物体信息的重建精度与重建算法的精确性息息相关。为了克服数字全息记录过程中手工选取滤波区域以及记录的高频成分信息丢失而造成的非实时性问题,采用了基于同态信号处理[16]的广义线性重建算法对全息图进行重建。同态信号处理是基于线性系统的叠加与相乘原理基础上的,广义线性重建算法又是基于相乘的同态信号处理理论和技术的,其重建过程流程图如图2所示。

Fig.2 Flow diagram of the generalized linear reconstruction algorithm
在数字全息技术中,全息图的表达式可以写为如下形式:
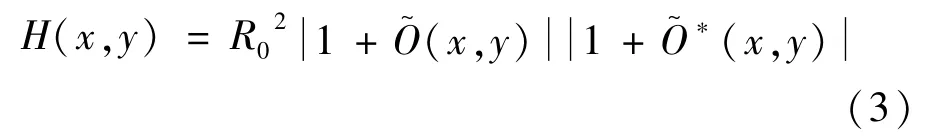
根据图2流程图所示,记录符合广义线性重建条件的全息图,对其作对数变换,得到ln[H(x,y)],再对其做傅里叶变换后得到全息图的频谱分布:

在图2所示的线性系统L中进行消噪、滤波处理,选取1/4谱面(一个象限)的频谱分布,即:
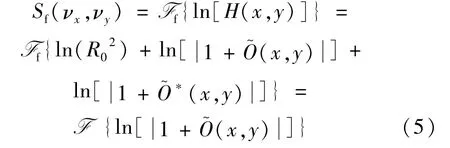
在利用基于同态信号处理的广义线性重建算法进行全息图的重建时,首先要保证参考光光强要远远大于物光光强,同时在频谱滤波时,要保证+1级频谱要分布在一个象限内,进而确保再现频谱选取的完整性。
3 实验验证
搭建了如图3所示的平面参考光预放大数字全息显微实验光路系统,对USAF1951空军分辨率测试板进行了实验研究。实验参量为:激光器的波长λ=632.8nm,CCD像素尺寸为4.65μm×4.65μm,16bit灰度级输出。25×MO的参量规格为:数值孔径为0.40,焦距为10.13mm,此MO的理论极限分辨率为0.97μm。图中,PBS(polarized beam splitter)、BS(beam splitter)、BE(beam expander)分别表示为偏振分光棱镜、消偏振分光棱镜、扩束准直系统。

Fig.3 Experimental setup of pre-magnification digital holography with plane reference wave

Fig.4 Intensity image of resolution target obtained by pre-magnification digital holography with plane reference wave
图4 是在图3所示实验光路系统基础上得到的实验记录结果。实验中选取的是25×的显微物镜,di=227mm,d=50mm,M=47.87。首先保证实验记录环境的稳定性,选取合适的物参夹角,使±1级和0级频谱恰好交叠,逐渐增强参考光强,记录全息图。图4a~图4c依次为记录的分辨率板的全息图、频谱分布图及由常规线性重建算法得到的强度再现像,图4d~图4h为通过广义线性重建算法得到的不同物光与参考光光强比值下的强度再现像。通过比较图4d~图4h可以发现:随着参考光与物光光强比值的不断增大,由广义线性重建算法再现得到的强度再现像得到了明显改善,如图4d~图4f所示。但当参考光与物光光强度比值增大到一定(再现像达到最优如图4g所示)后再继续增大这一比值,再现像质则趋于下降,如图4h~图4i所示。将对(5)式做逆傅里叶变换后得到的对数函数进行泰勒展开。根据泰勒展开式的特点分析可知:当<1且选取的项数一定时,)的值选取得越小,得到的计算精度才能越高,即随着参考光与物光光强比值的不断增大,利用非线性重建算法得到的再现像质量得到明显改善,但是参考光与物光光强比值达到一定值后,若继续增大该比值,得到的再现像的成像质量则变差,这是由于参考光太强,造成了参考光与物光的振幅相差太大,干涉场基本呈现一片均匀的亮度,降低了干涉条纹的对比度,影响了再现像质量。其中图4d~图4i中参考光与物光强度的平均比值依次为3.3486,5.6541,5.7996,5.8660,5.9370和5.9865。通过比较图4c与图4g可以发现:由广义线性重建算法得到的分辨率板的再现像优于常规线性重建得到的结果,图4g图再现像的像质比较均匀,图4c图则是在常规重建时由于0级谱滤除得不彻底或者高频成分的丢失等原因,影响了系统的成像分辨率。广义线性重建通过直接选取+1级谱所在象限进行强度重建,避免了由于手工选取滤波区域及部分高频成分丢失而造成的再现非实时性等问题,且有效地抑制了0级谱对再现像的干扰。在MATLAB 2010a环境下,采用常规线性重建算法进行强度再现时,除去手动选取滤波区域的耗时外,其它重建所用时间为1.681116s,广义线性重建过程中共耗时1.910704s。
4 结 论
通过理论分析与实验验证相结合的方法,对基于同态信号处理的广义线性重建算法的记录条件进行了优化,记录了不同物光与参考光光强比值下的全息图,利用广义线性重建算法对比分析了不同物光与参考光光强比值对数字全息再现像质的影响,提高了全息重建精度。结果表明,在参考光与物光光强比值不断增大的情况下,利用广义线性重建得到的再现像质量得到了明显改善,但当参考光与物光光强比值增大到一定比值时,再现像质量则开始下降。
[1] DAS B,YELLESWARAPU C S,RAO D V.Quantitative phase microscopy using dual-plane in-line digital holography[J].Applied Optics,2012,51(9):1387-1395.
[2] REN Zh,FAN Z B,LI JCh,et al.Precision measurement of mini-rotating-angles based on digital holography and its application[J].Laser Technology,2012,36(6):798-801(in Chinese).
[3] LIG Y,YANG Y.Digital holography particle image velocimetry applied for measurement of the rotating flow fields[J].Chinese Journal of Lasers,2012,39(6):0609001(in Chinese).
[4] ZHAO J,WANG D Y,LIY,et al.Experimental study on the quantitative phase contrast imaging of the biological samples by digital holographic microscopy[J].Chinese Journal of Lasers,2010,37(11):2906-2911(in Chinese).
[5] KEMPER B,VOLLMER A,ROMMELCE,etal.Simplified approach for quantitative digital holographic phase contrast imaging of living cells[J].Journal of Biomedical Optics,2011,16(2):60141-60144.
[6] KIM M K.Principles and techniques of digital holographic microscopy[J].SPIE Reviews,2010,11(1):018005.
[7] PARK Y,CHIOW,YAQOOB Z,et al.Speckle-filed digital holographic microscopy[J].Optics Experss,2009,17(15):12285-12292.
[8] PAN X Ch,LIU C,ZHU JQ.Improved fienup’s iteration method for image reconstruction in digital holography[J].Acta Optica Sinica,2012,32(6):09002(in Chinese).
[9] PAVILLON N,ARFRIE C,BERGOEND I,et al.Iterative method for zero-order suppression in off-axis digital holography[J].Optics Express,2010,18(15):15318-15331.
[10] SEELAMANTULA C S,PAVILLONN,DEPEURSINGEC,et al.Exact complex-wave reconstruction in digital holography[J].Journal of the Optical Society of America,2011,28(6):683-692.
[11] WANG H Y,LIU F F,LIAOW,et al.Optimized digital microholographic imaging system[J].Acta Physica Sinica,2013,62(5):42081-42089(in Chinese).
[12] WANG H Y,LIU F F,SONGX F,etal.Characteristic analysis of digital holographic microscopy with pre-magnification[J].High Power Laser and Particle Beams,2013,25(6):1365-1369(in Chinese).
[13] WU YQ,YE Z L,WANH.Speckle noise suppression of reconstructed image based on dual-tree complex wavelet and anisotropic diffusion[J].Chinese Journal of Lasers,2013,40(4):09002(in Chinese).
[14] CUCHE E,MARQUET P,DEPEUSINGE C.Spatial filtering for zero-order and twin-image elimination in digital off-axis holography[J].Applied Optics,2000,39(23):4070-4075.
[15] COLOMB T,KUHN J.CHARRRIERE F,et al.Total aberrations compensation in digital holographic microscopy with a reference conjugated hologram[J].Optics Express,2006,14(10):4300-4306.
[16] YANG Y,XUE D X,GAIQ,et al.Suppression of zero-order image in off-axis digital holography based on homomorphic filtering[J].Optics and Precision Engineering,2012,20(9):1877-1882(in Chinese).
Effect of reference intensity ratio to object on reconstructed image quality in digital holography
SONG Xiufa1,YU Mengjie2,WANG Huaying1,2,LIU Zuoqiang2,GAO Yafei2,LIU Feifei2
(1.College of Science,Hebei University of Engineering,Handan 056038,China;2.School of Information&Electrical Engineering,Hebei University of Engineering,Handan 056038,China)
In order to improve the accuracy and speed of image reconstruction,the generalized linear reconstructing algorithm based on homomorphic signal processing was analyzed by combining theoretical analysis and experimental verification in the digital holographic microscopy.The experimental results of the same field under different reference intensity ratio to object were compared.The results show that:with the increase of the intensity ratio,the reconstruction image quality of the generalized linear reconstructed algorithm is improved obviously.However,the reconstructed image quality decreases when the ratio increases to a certain value.Finding an appropriate ratio is important for obtaining high quality reconstructed images for the generalized linear reconstruction algorithm in digital holography.
holography;linear reconstructing;reference light intensity;homomorphic signal processing
O438.1
A
10.7510/jgjs.issn.1001-3806.2014.06.029
1001-3806(2014)06-0859-04
国家自然科学基金资助项目(61077001;61144005);河北省自然科学基金资助项目(F2010001038;F2012402051);河北省科技支撑计划资助项目(09277101D);河北省高等学校科学技术研究重点资助项目(ZH2011241)
宋修法(1960-),男,硕士,副教授,主要从事光学信息处理方面的研究。
E-mail:songxiufa@126.com
2013-10-17;
2013-12-09
