基于图论最小割集算法的图像分割研究
2014-06-23李白燕
张 健,李白燕
(黄淮学院信息工程学院,驻马店463000)
基于图论最小割集算法的图像分割研究
张 健,李白燕
(黄淮学院信息工程学院,驻马店463000)
为了提高图像分割的质量,采用图论最小割集算法进行了研究。首先将图像中的像素点映射为图论节点,节点权值通过平衡因子与共享最近邻节点数的比率计算;然后基于最小化能量方程建立图像最小割集,提取分割块内的灰度值作为块特征向量,用最小生成树对图分割;接着用判定函数判断临近区域是合并或者分割;最后给出了算法流程。结果表明,该算法可以分割出目标信息,并且算法鲁棒性好、峰值内存小。
图像处理;最小割集;权值;最小生成树
引 言
图像分割是将图像细分为多个图像子区域(像素的集合)的过程[1],把感兴趣的图像目标区域从不同区域的背景区域中提取出来,从而为下一步处理奠定基础。
图像分割方法有阈值分割法(threshold method,TM)、小波分析法(wavelet analysis method,WAM)、区域生长法(region growing method,RGM)、分裂融合法(fission and fusion method,FFM)、数学形态学法(mathematical morphological method,MMM)、多尺度法(multiple scales method,MSM)、马尔可夫随机场模型法(Markov random field model method, MRFMM)、水线法(waterline method,WM)等[2]。阈值分割法较其它方法具有直观性、易于实现、性能稳定等性质,使其被广泛地应用,但是存在计算量较大的缺点[3]。小波和阈值结合算法有较强的抗噪声性能[4],很难有效地选择阈值,后来出现硬阈值法和软阈值法,但是经过硬阈值函数处理后在正负阈值处不连续,软阈值方法通常会丢掉某些特征,分割图像会产生剧烈震荡。模糊集聚类的阈值方法(fuzzy threshold clustering method,FTCM)把背景与目标进行划分[5],聚类样本不需要训练集,但对初始分割需要提供一个初始参量,同时仍需多次迭代,花费大量的运算时间。最大类间方差的阈值方法(Otsu threshold method,OTM)选取类间最大方差的灰度值为最佳阈值[6],计算简单,但是当背景与目标灰度相差不大,会出现黑色区域,只对类间方差是单峰的图像有较好分割效果。
本文中采取图论最小割集算法(graph theoryand minimum cut set,GTMCS)对图像分割,首先图像中的像素点映射为图论节点,节点权值通过平衡因子与共享最近邻节点数的比率计算;然后基于最小化能量方程建立图像最小割集,提取分割块内的灰度值作为块特征向量,最小生成树对图分割;接着判定函数判断临近区域是合并或者分割;最后给出了算法流程。实验仿真显示本文中的算法能分割出目标信息,且算法鲁棒性好、峰值内存小。
1 算法描述
1.1 基于图论的图像表示
在图论中通过第i个节点vi以及连接不同节点间的第p个无向边ep构成几何图形,图像分割需要把图像的2维像素点映射到图论中。图像中的像素点映射图论节点vi∈V,集合V为所有节点集合;任意两个像素点对之间构成无向边e(vi,vj)∈E,标记为eij,集合E为所有边的集合;整幅图像对应的无向图表示为G=(V,E),每个无向边对应的相关权重w(vi,vj)∈W,标记为wij,集合W为所有无向边权重的集合[7];整幅图像对应的无向带权图表示为G=(V,E,W),其中节点权值通过平衡因子l∈(0,1)与共享最近邻节点数θi的比率计算:

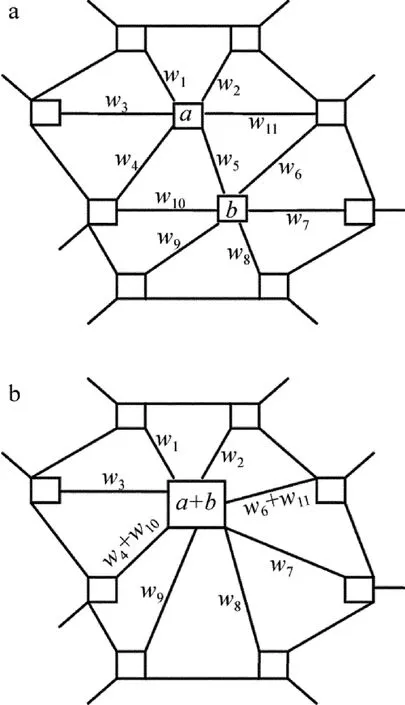
Fig.1 Optimization process
式中,wi表示vi的节点权值;θi表示vi与其它节点的共享最近邻数的总和[8]。
通过大图G0(V0,E0)构造更小规模的图Gi(Vi,Ei)进行优化,其中Vi+1包含的新节点数必须小于Vi。在优化匹配中,每条边的2个节点标记为Gi+1中的1个节点,不与匹配中任何边关联的节点可以直接标记为Gi+1的节点。例如当边(u,v)的2个节点u∈Vi,v∈Vi形成新节点h∈Vi+1,则新节点h的权为节点u和v的权之和,与新节点h关联的边的权为与u和v关联的边的权消除边(u,v)的权。如果某条边与u和v均关联,则这条边的权就是这些边的权之和[9],见图1。在图1a中,权w4,w10和权w6,w11分别独立,在图1b中,形成新节点关联的边的权为w4+w10和权w6+w11,其中权w5被消除,不与匹配中任何边关联的节点权可以直接标记,如w1,w2,w3,w7,w8,w9。
1.2 基于最小化能量方程的图像最小割集建立
由于图的节点对应了图像中的各个像素点,对图像的分割等价于将节点集V分割成不相交子集,分割表示为:

式中,i≠j,i,且j=1,2,…,k;k称为分割数目,Vi∩Vj=Φ。
提取分割块内的灰度值作为块特征向量,把块特征向量作为图论G的一个顶点vi,小块邻域的分块作为邻接顶点 vj,欧式距离计算边 eij的权值w(eij),然后最小生成树对图分割。对节点集V分割的目标是使分割后的子集同一类内节点像素间差异最小,不同分类间节点像素相异性最大[10]。若将图的所有节点分割成m个子集Vi,V2,…,Vm,其分割准则为:分割后的集合Vi内部节点间关联性和相似性大;不同子集Vi和Vj相互之间的关联性和相似性低。求最小生成树为:

式中,I(C)是类内差异,C1和C2是两个不同的分割域,D(C1,C2)是类间差异。
对W中所有节点i分配标记值xi,这样图像的前景和背景标记分别为xi=1和xi=0[11]。通过最小化能量方程解决:
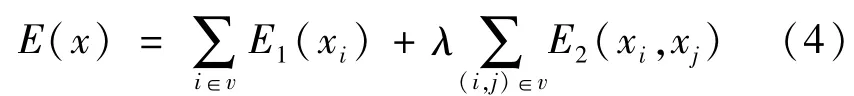
式中,E1(xi)为相似能量,表示将节点i赋值为xi的代价;E2(xi,xj)为先验能量,表示相邻节点i和j分别赋值为xi和xj的代价,λ为加权系数。
1.3 合并与分割判定函数
判定临近区域是合并还是分割的函数为:
式中,T为合并,F为不合并,π(C1,C2)是控制区域之间单位差别必须比最小的内部差别大的程度系统[12]。
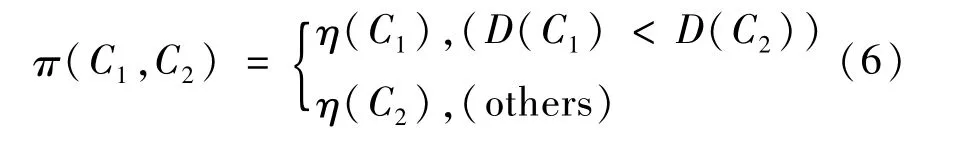
1.4 算法流程
(1)输入图像的像素点映射为图论节点,确定节点权重;(2)大图优化匹配为小图;(3)基于最小化能量方程建立图像最小割集;(4)判断合并条件,满足执行步骤(5),否则执行步骤(2);(5)k窗口可变尺度控制;(6)输出图像。
2 实验仿真
2.1 视觉分割效果
采用3种不同类型的经典图像:多峰模式Lena图像、双峰模式pout图像、单峰模式rice图像。不同算法仿真结果如图2~图4所示。
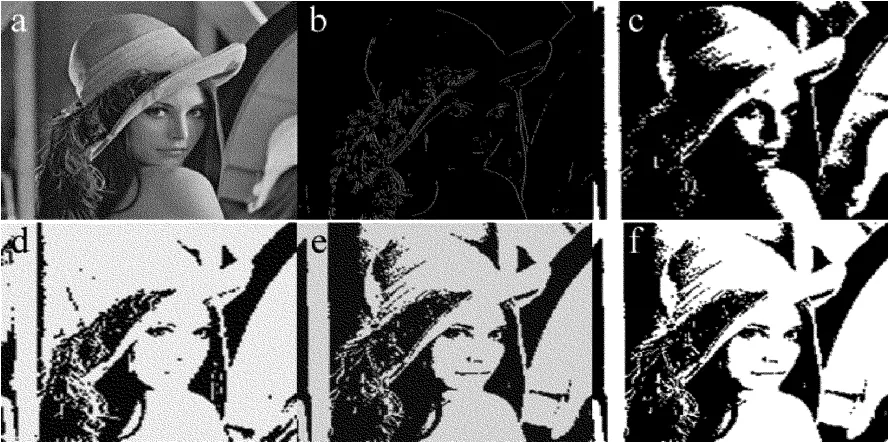
Fig.2 Simulation result of multimodal model Lena image of different algorithm

Fig.3 Simulation result of bimodal pattern pout image of different algorithm

Fig.4 Simulation result of unimodal pattern rice image of different algorithm
其中图2a、图3a和图4a为待分割的原始图像;图2b、图3b和图4b是阈值法分割效果;图2c、图3c和图4c是小波阈值法分割效果;图2d、图3d和图4d是基于模糊集聚类的阈值方法分割效果;图2e、图3e和图4e是基于最大类间方差的阈值方法分割效果;图2f、图3f和图4f是本文中算法分割效果。从分割效果上可以看出,本文中算法分割出目标信息,而其它算法分割出来的目标物体含有大量的背景信息,不能准确地分割出目标来。
2.2 鲁棒性分析
仿真图像灰度变化情况下图像分割的像素数目,设f(x,y)表示原始的图像在(x,y)点处的灰度值,灰度变化公式:

对原始Lena图像逐渐改变灰度,像素个数的对比指标来检验该算法是否具有鲁棒性,如表1所示。
从表1的分割像素数目可以看出,当外界图像灰度变化前后,本文中算法的效果仍是最稳定的,分割得到的目标像素个数差距最小,具有鲁棒性,而这一性质对于图像处理非常有意义。

Table 1 Pixels of image gray level before and after change
2.3 时间复杂度分析
为了比较算法的复杂度,表2中给出了运行时间和峰值内存(peak memory,PM)。
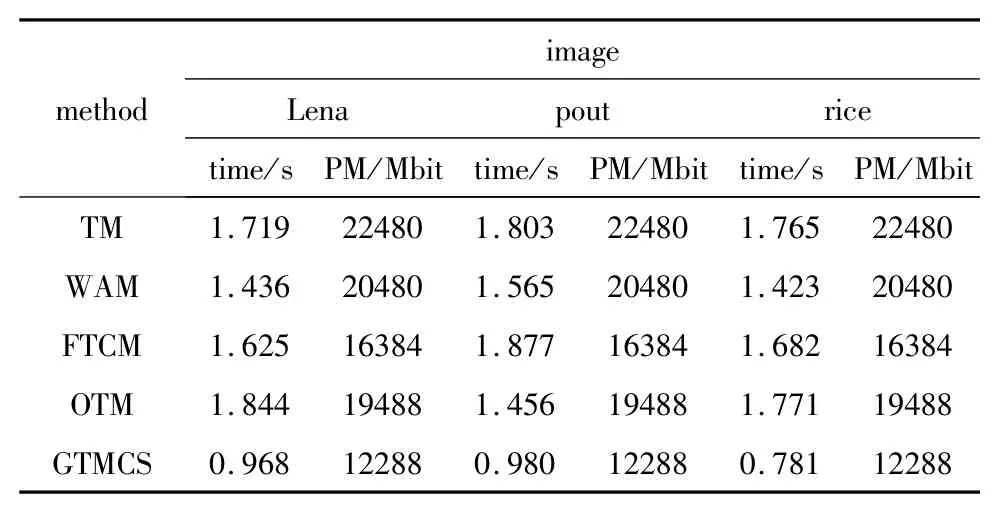
image method Lena pout rice time/s PM/Mbit time/s PM/Mbit time/s PM/Mbi t TM 1.719 22480 1.803 22480 1.765 22480 WAM 1.436 20480 1.565 20480 1.423 20480 FTCM 1.625 16384 1.877 16384 1.682 16384 OTM 1.844 19488 1.456 19488 1.771 19488 GTMCS 0.968 12288 0.980 12288 0.781 12288
本文中算法的运行时间少,所需的峰值内存小,对图像处理具有实时性。这是因为欧式距离计算边的权值,通过最小生成树对图分割。
3 小 结
采用图论算法把图像中的像素点映射为图论节点,节点权值通过平衡因子与共享最近邻节点数的比率计算;然后基于最小化能量方程建立图像最小割集,提取分割块内的灰度值作为块特征向量,最小生成树对图分割;判定函数判断临近区域是合并或者分割;最后给出了算法流程。实验仿真显示,本文中的算法可分割出目标信息,且算法鲁棒性好、峰值内存小。
[1] XU T J,QIAN X F,DAIX R,et al.Unwrapping algorithm based on segmentation and zooming for under sampled wrapped phase[J].Laser Technology,2014,38(1):39-43(in Chinese).
[2] WEIXE F,LIU X.Research of image segmentation based on 2-D maximum entropy optimal threshold[J].Laser Technology,2013,37(4):519-522(in Chinese).
[3] HUANG J,YUAN Zh W,TIAN Z Sh.Research on wavelet threshold function denoising of CDMA signal[J].Video Engineering,2013,37(7):75-78(in Chinese).
[4] LIK F,WANG Zh.Application of improved wavelet threshold denoising in speech recognition[J].Computer Technology and Development,2013,23(5):231-234(in Chinese).
[5] CHEN Y X.Ant spatial clustering based on fuzzy if-then rule[J].Mathematics in Practice and Theory,2011,41(19):114-119(in Chinese).
[6] LIM,LUO H Y,ZHENG X L,et al.Image segmentation based on improved Otsu algorithm[J].Journal of Nanjing University of Science and Technology,2012,36(2):332-337(in Chinese).
[7] HONG H Y,YAN L X,GUO X Y,et al.Approach to extract moving targets from production line under complex scenes[J].Journal of Huazhong University of Science and Technology,2012,40(7):57-61(in Chinese).
[8] XIE Y Sh,FAN X P,LIAO Zh F,et al.Weighted cluster fusion algorithm based on graph[J].Application Research of Computers,2013,30(4):1015-1016(in Chinese).
[9] JINGGQ,CHEN DW.A finite element nodal ordering with algebraic graph theory[J].Journal of Tongji University,2010,38(6):929-934(in Chinese).
[10] MENG Q T.Segmentation algorithms based on the natural scene graph and clustering image[D].Suzhou:Soochow University,2010:32-46(in Chinese).
[11] WANG X S,ZHOU M Q,FAN Y CH,et al.The algorithm of graph cut using HSI weights in color image segmentation[J].Journal of Image and Graphics,2011,16(2):221-226(in Chinese).
[12] CUIB G,MENG A X.Fast remote sensing image segmentation algorithm based on nearest neighbor direct graph[J].Computer Science,2013,40(10):274-278(in Chinese).
Research of image segmentation based on graph theory and minimum cut set algorithm
ZHANG Jian,LIBaiyan
(College of Information Engineering,Huanghuai University,Zhumadian 463000,China)
In order to improve the quality of image segmentation,graph theory and minimal cut set algorithm were used.Firstly,using the pixel points of image as the mapping nodes of the graph theory,the node weight were calculated by the ratio of the balance factor and the shared nearest neighbor nodes.Then,the minimum cut set of the image was established based on the minimized energy equation,the gray value of the segmentation block was extracted as the block feature vector and the image was segmented by minimum spanning tree.The adjacent regions were judged to be combined or to be segmented by judging function.Finally the algorithm flow was given.The results show that the target information can be segmented by this algorithm.This algorithm has good robustness and small peak memory.
image process;minimum cut set;weight;minimum spanning tree
TN911.73
A
10.7510/jgjs.issn.1001-3806.2014.06.030
1001-3806(2014)06-0863-04
张 健(1980-),男,硕士,讲师,研究方向为信号处理、智能控制。
E-mail:hhzhj@foxmail.com
2013-12-25;
2014-03-07
