磁悬浮飞轮微振动特性及其主动振动控制方法研究*

孟 猛，樊亚洪，2，张激扬，2，刘 虎，邓晓楠

(1.北京控制工程研究所，北京 100190;2.航天器先进惯性执行机构与测量技术联合实验室，北京 100190;3.北京航空航天大学仪器科学与光电工程学院，北京 100191;4.中国空间技术研究院，北京 100094)

O 引言

磁悬浮飞轮具有无接触、无摩擦、无需润滑、高精度、长寿命等优点［1］.从理论上磁悬浮飞轮可以达到无振动，但是实际中仍存在一些扰动源会引起振动，进而传递到星体上.引起这些扰动的原因，包括不平衡振动、传感器噪声、定转子固有模态振动以及安装误差等.这些扰动会造成磁悬浮飞轮惯性矢量产生误差，从而影响卫星的姿态稳定精度和指向精度［2］.

本文利用微振动测量平台和数据采集分析硬件和软件，实时测量飞轮两个平动方向的微振动力，通过分析磁悬浮飞轮微振动力时域特性和频域特性，特别是通过分析瀑布图，找出引起磁悬浮飞轮微振动的主要频域分量，例如同频量、倍频量或者不随转速变化的模态量.运用主动振动控制算法对相应频域分量进行控制，最终实现在时域和频域飞轮振动力的显著下降.

1 磁悬浮飞轮结构及建模

磁悬浮飞轮磁轴承转子动力学建模的建立是磁轴承控制方法研究的基础［3］.

1.1 飞轮结构

本文测试用的飞轮的结构如图1所示.磁轴承系统由上、下两个轴向磁轴承和一个径向磁轴承组成.与典型结构磁轴承系统的控制方式不同，径向磁轴承只产生转子径向平动控制力，转子的径向偏转控制力矩和轴向平动控制力均由轴向磁轴承产生［4］.

图1 五自由度磁悬浮飞轮结构示意图Fig.1 Structure of 5 DOF MSFW

1.2 转子动力学模型

假设飞轮转子为刚性转子，质量为m，极转动惯量为JP，赤道转动惯量为Je.建立转子坐标系统OXYZ，如图2的转子坐标系统所示，转子绕Z轴旋转，转速为Ω，绕X，Y轴的转角分别为α，β，转子对应于3个惯性主轴的转动惯量分别为JX，JY，JZ，则有JZ=JP，由于转子为轴对称结构，因而有JX=JY=Je.

除了Z轴的转动，转子动力学方程可写为

其中式(1)为转子的3个平动方程，式中FX、FY、FZ为作用于转子质心上的外力在X方向、Y方向和Z方向上的分力.式(2)为转子的两个转动方程，式中MΑ和MΒ为作用于转子上绕X轴和Y轴的外力矩.

图2 转子坐标系统Fig.2 Coordinate system of rotor

对于图1所示的磁悬浮飞轮结构，径向偏转两个自由度是靠轴向平动的4个分量z1，z2，z3，z4来控制，与偏转关系如下:

其中R为转子半径.

FX、FY、MΑ、MΒ为作用在转子质心上的外力和力矩，本身是非线性的，但是当转子在平衡位置附近作小范围位移运动时，可以做Taylor展开得到近似的线性方程［1］:

其中，KS为位移刚度系数，Ki为电流刚度系数，Ii为控制电流，q为转子平动位移和偏转.

1.3 转子微振动模型

含有不平衡量的转子中心面如图3所示.由于转子静不平衡量的存在，转子几何中心与质心不重合.

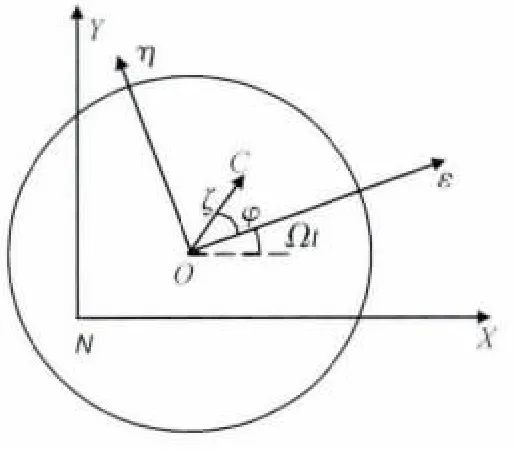
图3 转子中心面坐标系统Fig.3 Coordinate system of central rotor plane

以磁轴承转子质心O为原点建立相对于惯性空间的固定坐标系(NXY).其中λ为几何中心和质心的长度，Ωt+φ为旋转角度.将转子静不平衡量作为系统内部扰动，考虑磁轴承转子处几何中心和质心之间的相对位置关系，有:

式中:X'，Y'分别表示几何轴在磁轴承处的位移和偏转;x'，y'分别表示惯性轴在磁轴承处的位移和偏转.

当转子在平衡位置附近小范围运动时，根据式(4)，轴承力的线性化方程为

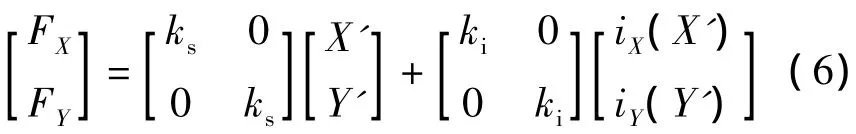
式中:iX、iY为相应的磁轴承控制电流;ks为磁轴承的位移刚度;ki为磁轴承的电流刚度.由式(6)可见，轴承力中的位移刚度分量和电流刚度分量均存在不平衡扰动.

令

则由式(6)、(7)可得含不平衡扰动的径向磁轴承力方程为

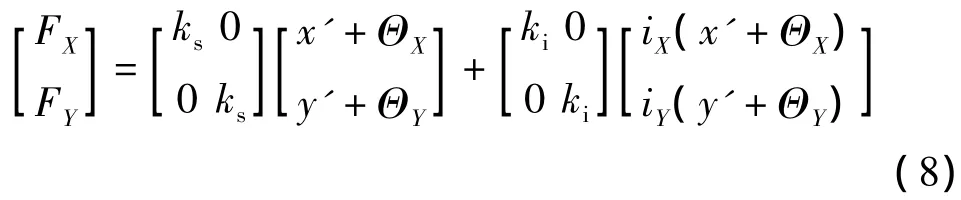
其中ΘX、ΘY表示因不平衡量引入的扰动.

由1.2节可知，磁悬浮飞轮结构特殊，径向偏转两个自由度通过轴向磁轴承控制.因此，其偏转自由度的不平衡量模型不同于传统结构的磁轴承转子，如图4所示.

图4 中 z1，z2，z3，z4为轴向平动的 4 个分量，以z1，z3方向为X轴，z2，z4方向为Y轴，Z轴为转子惯性轴.R'为定子下平面半径，δ为转子中心距定子下平面的间隙.由此可以推导出转子中心面边缘距定子下平面的最小间隙lmin为

图4 转子结构示意图Fig.4 Structure of the rotor

Ωt+φ是z1磁轴承相对于最小间隙lmin旋转过的角度.由此可以推导出 z1，z2，z3，z44 个轴向磁轴承间隙如下式:

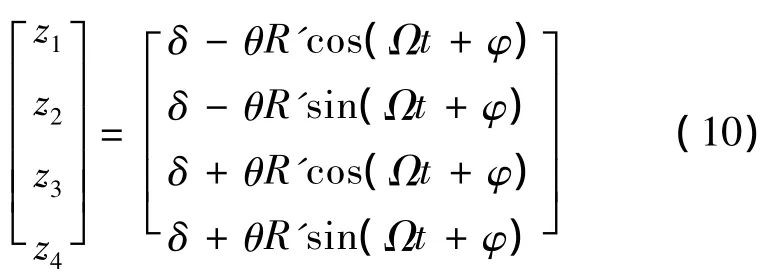
令

其中ΘΑ(t)和ΘΒ(t)为转子的不平衡扰动量.则由式(10)、(11)可得含不平衡扰动的轴向磁轴承力方程为

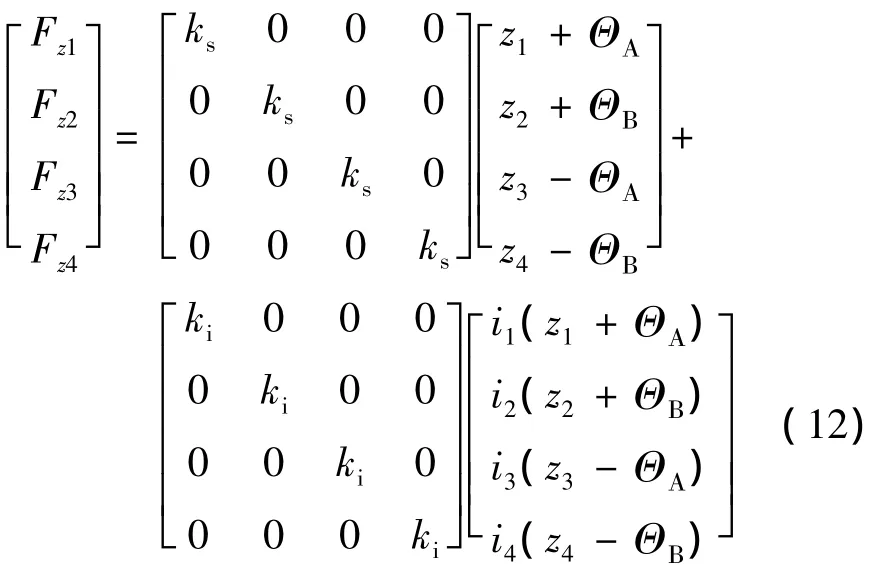
除了转子不平衡量，传感器误差也是引起振动的扰动源.磁轴承转子的倍频分量主要是由传感器奇次谐波导致的［5］，包含倍频分量的磁轴承转子的广义位移方程可写为

其中ε'为传感器误差引入的倍频分量.

2 微振动测试

2.1 测试系统简介

微振动测试系统如图5所示，测试过程中磁悬浮飞轮固连在基座上，利用压板将飞轮和基座压紧在测量台上，从而确保飞轮、基座和测振台成刚性安装.由于不同的安装位置会影响两个偏转方向振动力矩的测量，因此本文主要针对两个平动方向的振动力作测量和控制，尽量避免因安装方式引起的测量误差对控制效果的影响.

图5 微振动测试系统Fig.5 Micro-vibration test system

2.2 测试结果与分析

本节对磁悬浮飞轮的测试，磁轴承反馈控制回路只是保留了基本的PID控制和交叉算法以保证系统的稳定性.目的是考查无主动振动控制算法的情况下磁悬浮飞轮的振动力的时域和频域特性.测试过程中磁悬浮飞轮以0.05 N·m的力矩从0 r/min升至5200 r/min.径向平动X和Y两个方向的振动力FX和FY的瀑布图如图6～7所示.瀑布图中3个坐标轴分别是频率、转速和力.

从图6和7中可以看出，径向平动两个方向振动力FX和FY的同频分量和5倍频分量在整个频谱范围内比较明显.其中5倍频分量在3000 r/min以后的高速时有非常明显的上升.从两个平动方向振动力的时域图(如图8)，可以看出，在整个升速过程中FX和FY的振动力的时域值一直上升，到4500 r/min的高速时稳定在±10 N和±15 N.

图6 径向平动X方向的振动力瀑布图Fig.6 Waterfall diagram of radial X direction

图7 径向平动Y方向的振动力瀑布图Fig.7 Waterfall diagram of radial Y direction

图8 径向平动X，Y方向振动力时域图Fig.8 Vibration force of X and Y radial directions in time domain

因此，如果将FX和FY的同频分量和5倍频分量进行有效控制，那么其振动力在时域和频域都会有很明显地下降.这就是下一步作主动振动控制的目的.

3 主动振动控制方法及效果

3.1 主动振动控制方法原理

(1)同频闭环陷波

由含有不平衡扰动的轴承力方程(8)可以看出，要完全抑制不平衡扰动的影响，首先要辨识并滤除控制电流中的同频分量，即确定ΘX(t)和ΘY(t)并补偿.方法如下:将式(7)改写为(只针对径向平动)

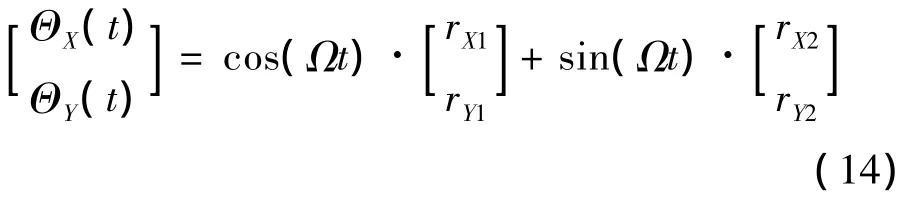
式中，rX1，rX2为同频扰动余弦分量幅值，rY1、rY2为同频扰动正弦分量幅值［1］，如图9所示.N(s)是中心频率随转速变化的自适应陷波器;Nf(s)是跟踪滤波器;ε是反馈系数，决定自适应陷波器N(s)的收敛速度和中心陷波带宽，w(t)和c(t)为陷波器输入输出.

经闭环反馈系统收敛后［5］，滤波器Nf(s)中积分器的输出值即为转子位移信号中正余弦同频分量幅值，也就是实现了对电流信号中不平衡量的辨识及补偿.

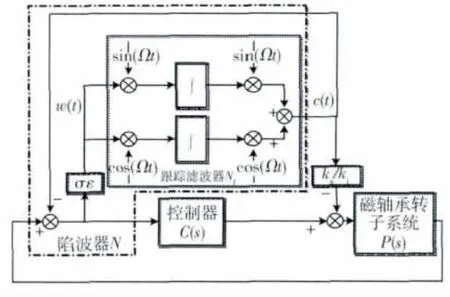
图9 主动振动控制方法框图Fig.9 Block diagram of adaptive vibration control

(2)位移刚度补偿

由式(8)可知，在滤除控制电流同频扰动分量之后，还必须对位移刚度力中的同频分量进行补偿，即在各磁轴承控制电流中分别加入位移刚度力补偿项:

其中位移刚度ks和电流刚度ki均可以通过试验测得.

(3)同频开环陷波

闭环自适应陷波的引入必然会改变原闭环系统的传递函数和稳定性.通过稳定性分析，当飞轮转速大于临界转速时，系统才是稳定的，否则系统会失稳［6］:

ω0是与控制系统参数相关的临界转速［7］.

(4)倍频分量的抑制方法

倍频量的扰动方程为

倍频分量的补偿控制可采用自适应跟踪滤波器和陷波的方法来实现，只要从传感器信号中滤除相对惯性轴的倍频干扰即可.

3.2 控制效果

(1)同频分量

如图10，加入振动控制算法后，FX的同频分量的峰值从约为4 N下降到0.7 N左右，降幅约为83%;FY之前的同频分量峰值约为3 N，之后约为0.8 N，降幅约为73%.

图10 径向平动X、Y两个方向振动力同频分量Fig.10 Same frequency componentin X and Y radial direction

(2)倍频分量

FX的5倍频分量的峰值从大约2.3 N，下降到不足0.3 N，降幅约为87%;FY的5倍频分量的峰值从7 N下降到不足1.5 N，降幅达79%，如图11所示.

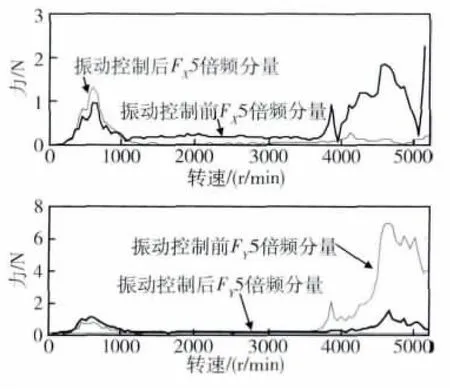
图11 径向平动X、Y两个方向振动力5倍频分量Fig.115-times frequency component in X and Y radial directions

(3)振动力时域值

对比图12与图8，未加任何振动控制算法时，FX和FY的时域值在整个升速过程总有很明显地上升，最终维持在±15 N和±20 N左右，加了主动振动控制算法后的整个升速过程中的时域值基本维持在±5 N以内.

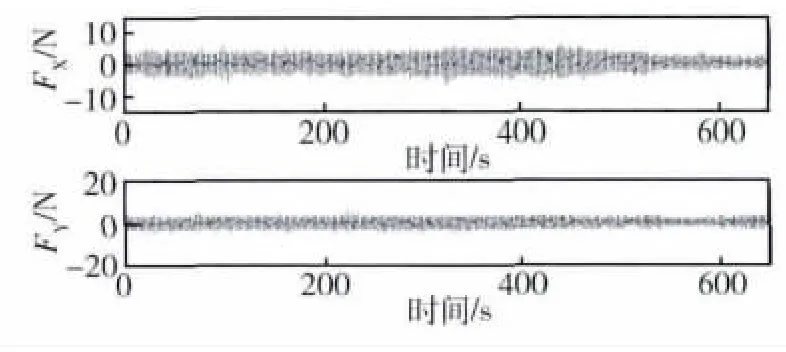
图12 径向平动X、Y方向振动力时域图Fig.12 Vibration force diagram of X and Y radial directions in time domain

4 结束语

本文通过测试磁悬浮飞轮的微振动特性，发现磁悬浮飞轮除了同频量、倍频量和不随转速变化的模态分量，基本无其他频域分量.并且由于交叉反馈控制，也看不到章动和进动分量.在时域特性上，振动力时域值会随着转速升高而增加，最终在高速时基本保持稳定.在对频域特性和时域特性分析的基础上，本文利用闭环自适应陷波，位移刚度补偿和开环自适应陷波的方法，将平动X，Y方向的同频和5倍频分量进行控制，降幅达均到70%以上，体现了主动振动控制算法的有效性.

本文后续仍然有很多工作需要深入研究，从整个瀑布图来看，需要滤除的频域分量还有不随转速变化的弹性模态分量、低速时的倍频分量等.另外，本文未考虑磁中心调零对控制效果的影响，也没有考虑不同的支撑刚度对于主动振动控制方法的影响，这些是下一步研究中要解决的主要问题.

［1］ 刘彬，房建成，刘刚，等.磁悬浮飞轮不平衡振动控制方法与试验研究［J］.机械工程学报，2010(6):188-194.LIU B，FANG J C，LIU G，et al.Unbalance vibration control and experiment research of magnetically suspended flywheels［J］.Journal of Mechanical Engineering，2010(6):188-194.

［2］ 房建成，孙津济，樊亚洪.磁悬浮惯性动量轮技术［M］.北京:国防工业出版社，2013:290-295.

［3］ HERZOG R，BUHLER P，GAHLER C，et al.Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings［J］.IEEE Transaction on Control System Technology，1996，4(5):587-586.

［4］ 刘虎，房建成.新型永磁偏置轴向磁轴承的磁力特性研究［J］.机械工程学报，2010，46(5):167-174.LIU H，FANG J C.Research on magnetic force characteristics of a novel permanent magnet biased axial magnetic bearing［J］.Journal of Mechanical Engineering，2010，46(5):167-174.

［5］ 樊亚洪.空间用磁悬浮动量轮磁轴承系统高稳定度高精度控制方法与实验研究［D］.北京:北京航空航天大学，2011.FAN Y H.Experimental research on high stability and high precision control of magnetic bearing system for magnetically suspended flywheel used in space［D］.Beijing:Beijing University of Aeronautics and Astronautics，2011.

［6］ 刘彬.五自由度全主动大力矩磁轴承悬浮动量轮磁轴承系统控制方法与实验研究［D］.北京:北京航空航天大学，2011.LIU B.Study on magnetic bearing control and experiments for a five active axes magnetically suspended flywheel with large torque capacity［D］.Beijing:Beijing U-niversity of Aeronautics and Astronautics，2011.

［7］ LI L C，SHINSHI T H，ZHANG X Y，et al.A simple method for rotation about the inertial axis of a rigid AMB rotor［C］//Proceedings of the 8thInternational Symposium on Magnetic Bearings.Mito，Japan，2002:405-410.