基于天线驱动组件的多体卫星MIMO控制及稳定裕度应用研究*

李信栋，苟兴宇

(1.北京控制工程研究所，北京 100190;2.空间智能控制技术重点实验室，北京 100190)

O 引言

多体卫星对星本体进行姿态控制的同时还要对各附件进行指向控制，两种控制回路之间必然存在运动学和动力学耦合，对于这种典型的多输入多输出(MIMO，multi-input multi-output)控制系统的稳定裕度分析不像单输入单输出(SISO，single-input sin-gle-output)线性定常系统那样简单.SISO线性定常系统的稳定裕度有明确的定义，而MIMO线性定常系统的稳定裕度分析方法仍在发展中.针对MIMO线性系统的稳定裕度，文献［1］提出多变量稳定裕度概念km(ω)，并基于映射理论通过迭代算法得到最终稳定裕度结果，但此法计算量大且结果保守;类似的，文献［2］提出的结构奇异值μ分析法也能得到较保守的稳定裕度估计结果，并且两定义间存在关系基于频域中的Nyquist理论，文献［3］提出了临界方向理论(critical direction theory)，并给出临界方向和临界扰动半径的概念，通过开环系统的特征函数得到整个系统Nyquist鲁棒稳定裕度;为了减小计算量，文献［4］根据奇异值理论，通过计算系统回差阵的奇异值来求取系统的稳定裕度;此外，文献［5］在文献［4］的基础上进行改进，提出一种基于逆回差阵奇异值的计算方法，将其与回差阵奇异值法相结合有利于减小稳定裕度计算结果的保守性.

为使多体卫星系统的控制策略和稳定裕度的计算结果更具有工程参考价值，本文采用工程中的天线驱动组件(GDA)为天线指向提供驱动力矩;在天线小角度机动条件下，针对两输入两输出的多体卫星线性控制系统，采用多变量频域理论中的序列回差设计技术，设计卫星本体俯仰姿态和天线指向控制的MIMO控制器，并利用Nyquist稳定判据证明整个闭环系统的稳定性;在此基础上分别利用回差阵奇异值法和逆回差阵奇异值法计算MIMO控制系统的稳定裕度，将两者所得结果进行比较并结合起来使用，达到减小稳定裕度计算结果保守性的目的.

1 系统动力学建模

将附件天线的惯性特征与卫星中心刚体结合在一起，可以得到多体卫星系统的两刚体动力学构型，如图1所示.定义φ、θ、ψ分别为航天器的滚动、俯仰、偏航姿态角，图中定义了卫星本体固连坐标系XYZ的方位，并将天线在标称零位锁定时的天线固连坐标系方位定义为经卫星本体固连坐标系 +X 轴旋转180°得到［6-7］.

定义天线绕X轴、Y轴的转动角分别为α、β，运用Newton-Eular法，以1x－2y转序为例，利用各坐标系之间的关系导出标量动力学方程.在平台姿态可以线性化、平台与附件机动角速度均不大的前提下，进一步将控制对象简化为俯仰平面问题，相应标量格式的动力学方程［6-7］为

图1 平台+天线的两刚体构型Fig.1 Two-rigid-body system with platform and appendages

式中，Ia，yy和 Ib，yy分别为航天器平台与天线绕各自俯仰轴的转动惯量，xra，cc，cs为系统几何参数所决定的常系数，ma为天线质量，Mcy为绕航天器y轴的俯仰姿态控制力矩，Mβ为β转角控制力矩.

若考虑GDA作为天线驱动执行机构，可得天线驱动力矩 Mβ［7］为

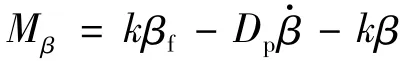
其中，k为等效弹簧刚度，Dp为等效弹簧阻尼系数，βf为天线指令输入转角，则系统模型(1)可变为

假设天线指向角在俯仰平面内小角度机动，即在β=0°附近考虑问题，则动力学方程进一步变为

选择输入u= [ Mcyβf]T，输出 y=[θ β]T，对式

(3)进行拉氏变换可得对象传递函数矩阵为

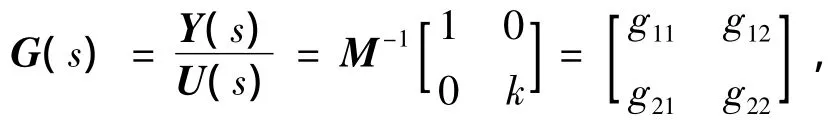
其中

2 序列回差控制器设计及稳定性分析

序列回差设计法是英国学者Mayne首先提出的［8］.这种方法的基本思想是将多变量反馈控制系统化为单回路，通过顺序的闭合每一个回路设计相应控制器，并判断稳定性，直至闭合最后一个回路，最终得到整个系统控制器.

序列回差法设计的控制器可写成如下形式:

式中:Ka是常数置换矩阵，满足是一系列初等列运算矩阵的乘积，即

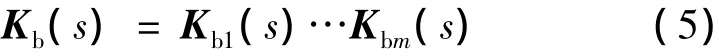
这里每一个Kbi(s)代表一次列运算;Kc(s)是非奇异对角阵

要求每个对角元素kci(s)的所有零点、极点均在s平面的左半开平面内，kci(s)即为闭合第i个回路时所要设计的反馈控制器.

定理1［8］.设对象传递函数矩阵G(s)是非奇异的有理传递函数矩阵不恒为零且G(s)是稳定的，那么一定存在一个置换矩阵Ka和补偿矩阵Kb(s)，使Q0(s)=G(s)KaKb(s)是非奇异的对角优势阵，且对角元素所有极点和零点均在左半开平面内.

这个定理说明闭合第i个回路并不影响其他前i－1个回路，这表明逐次选择 Kb(s)=Kb1(s)…Kbm(s)的各因子，可使Qi－1(s)的第i个对角元素的极点和零点均在左半开平面内，更有利于第i个回路的反馈控制器kci(s).

定理2［8］.如果控制对象G(s)是稳定的，则选择每一个kci(s)和Kbi(s)，使它们的零、极点都在s平面的左半开平面内.逐次闭合每一个回路所得子系统νi，做对应于每一个子系统的标量回差ti(s)的奈氏轨迹，若它不包围或不通过s平面的坐标原点，则子系统νi是稳定的，整个系统也是闭环稳定的.

对本文的对象进行设计，根据定理1，第一步选择常数阵Ka，一般令Ka=I2，I2为2×2维单位阵.进一步设计控制器Kb(s)，这里控制器Kb(s)的目的是使系统未闭合的部分成为对角优势，可选择

计算Q0(s)=G(s)KaKb1(s)，得

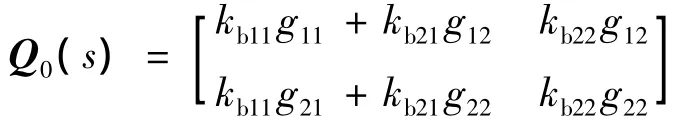
判断其有没有零、极点在右半平面内，作它的Nyquist图，如图2所示.从图中可看出Nyquist图不包围且不通过s平面的坐标原点，因此闭合第一个回路后得到子系统ν1是稳定的.其闭环传递函数矩阵为

现在设计第二个回路.由Kb2(s)的结构形式所决定，只能选择Kb2(s)=I2，则有Q1(s)=G1(s)，选择控制器 kc2(s)，计算此时回路的标量回差t2(s):

同样对t2(s)作Nyquist曲线如图3所示，判断其是否不包围且不通过s平面的坐标原点，由图3可看出t2(s)对应的系统是稳定的.

根据定理2，标量回差t1(s)和t2(s)的Nyquist图都不包围且不通过s平面的坐标原点，因此，最后可证得整个闭环系统是稳定的.

图3 t2(s)的Nyquist图Fig.3 Nyquist diagram of t2(s)

到此为止，各控制器设计已经完成，根据式(5)和(6)可知它们分别为

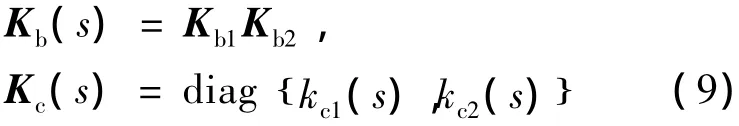
由式(4)和(9)可得总控制器为

3 稳定裕度分析

针对本文的多体卫星MIMO控制系统，分别利用回差阵奇异值法［4］和逆回差阵奇异值法［5］计算MIMO控制系统的稳定裕度，两者相结合来减小稳定裕度计算结果的保守性.对一般反馈控制系统如图4所示，其中G(s)∈Cn×n为系统标称模型.与文献［5］中所示不同，这里在输出端引入不确定性量测阵，令 s=jω ，有

下面分析系统保持稳定所容许各回路增益或相角变化的最大值，具体通过不确定量测阵P(s)中的参数ki和φi来获取系统稳定裕度.

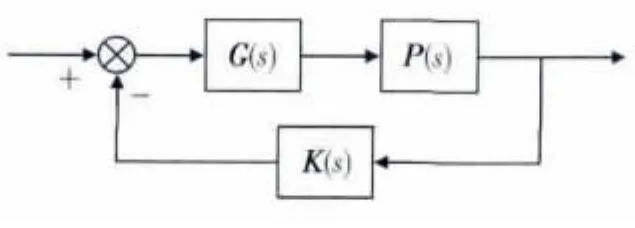
图4 一般反馈系统模型Fig.4 Feedback control system

3.1 回差阵奇异值法

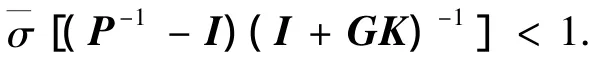
若考虑增益和相位在每个通道同时变化的情况，由方程(12)，可得系统稳定的充分条件为

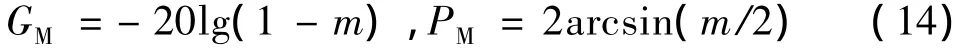
本文中的系统模型是简化后的两输入两输出线性模型，设计控制器完毕后引入量测阵P(s)如图5所示，计算其回差阵［I+G(s)K(s)］，然后通过Matlab仿真工具可求得回差阵在整个频带范围内最小奇异值为min(I+GK)=0.6197 ，根据式(14)可得相应的稳定裕度为:当所有通道的幅值不变时，允许所有通道的相位裕度是36.1°;当所有通道的相位不变时，允许所有通道的幅值裕度是8.4 dB.

图5 引入量测阵后控制系统框图Fig.5 Feedback control system with measurement matrix

3.2 逆回差阵奇异值法

假设标称系统是可逆的，即［G(s)K(s)］－1存在，若标称系统闭环稳定，则有［I+(GK)－1］＞0，在输出端引入不确定量测阵P(s)后系统仍保持稳定的条件［I+(PGK)－1］＞0，利用矩阵分离特性:

根据P(s)的定义，可知P－1(s)存在，而I+(GK)－1亦是非奇异的，因此(P － I)［I+(GK)－1］－1+I必须非奇异，可知其为非奇异的一个充分条件是:

联系式(15)，令不等式(16)右边项小于1，得到系统稳定的充分条件为

若考虑增益和相位在每个通道同时变化的情况，根据P(s)的定义式，可得系统稳定的充分条件为

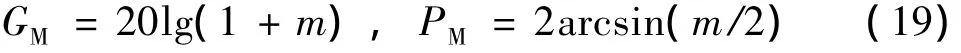
针对本文中的线性化模型，计算其逆回差阵I+［G(s)K(s)］－1，通过仿真工具可求得逆回差阵最小奇异值为min［I+(GK)－1］=0.7594，根据式(19)可得相应的稳定裕度为:当所有通道的幅值不变时，允许所有通道的相位裕度是44.63°;当所有通道的相位不变时，允许所有通道的幅值裕度是4.9 dB.

虽然两种方法都计算得到系统稳定裕度，但是分析两者的结果可看出，逆回差阵奇异值法所得的相位裕度结果有所改善，但是增益裕度结果相对减小，两种方法都具有较大保守性;因此，将两种方法的稳定裕度结论综合起来考虑，分别比较两种方法所得增益裕度和相位裕度的大小，则它们之间的较大者可作为本文控制系统的最终稳定裕度，即系统仍能保持稳定所允许的所有回路中增益可同时增大8.4 dB，相位角可同时滞后 44.63°.

4 数值仿真

针对卫星本体俯仰轴姿态运动和天线指向角运动同时跟踪情况下的MIMO控制系统进行仿真分析，绘制仿真图，以验证上文所设计的控制器的有效性.在本文中，对象模型参数取 Ia，yy=0.438 kg·m2，Ib，yy=3453 kg·m2，ma=8 kg，cc= －1.94 m，cs= －0.22 m，xra= －0.0056 m，Dp=0.95 N·m·s/rad，k=175 N·m/rad，则线性动力学方程为

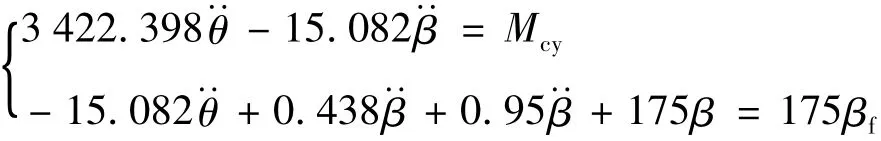
文中所设计控制器为

采用如式(20)所示的控制器对式(2)所示原始非线性模型进行仿真，并且令各状态量的初始值为θ0=β0=0°.设计卫星本体俯仰轴姿态期望跟踪轨迹和卫星天线指向角期望跟踪轨迹分别为

得到仿真结果如图6所示.

通过仿真结果可以看出，俯仰姿态和天线指向角能较快地跟踪期望轨迹，两者跟踪误差最终都趋于较小值;同时能保证一定的姿态控制精度和天线指向精度，因此所设计控制方法使系统具有较好的跟踪效果，控制器满足设计要求.

图6 星本体俯仰姿态和天线指向角的跟踪误差曲线Fig.6 Tracking errors of satellite pitch attitude and antenna pointing angle

下面对第3节中所求稳定裕度结果进行仿真验证.根据计算结果已知系统各回路增益可同时增大8.4 dB，即增大至2.63倍.采用上文设计的控制器对式(2)所示非线性模型进行仿真，可得系统的跟踪误差曲线图如图7所示.从图中可以看出，天线指向角误差曲线已有发散趋势，说明系统已经不稳定.

分析出现这种情况的原因认为:系统的稳定裕度是对线性化后的线性MIMO系统分析得到的，而图7所示仿真是针对式(2)所示原始非线性模型进行的，因此，稳定裕度的结果不可避免的有所偏差.下面适当减小回路增益所增大的倍数，令所有回路增益同时增大至2.56倍，继续进行仿真，并得到仿真结果如图8所示.

图7 系统增益增大至2.63倍时的跟踪误差曲线Fig.7 Tracking errors with the gain increasing to 2.63 times

图8 系统增益增大至2.56倍时的跟踪误差曲线Fig.8 Tracking errors with the gain increasing to 2.56 times

从图8中可以看出，系统误差没有明显发散趋势，系统是稳定的.分析上述验证结果可知，针对线性化后的线性MIMO系统分析得到的稳定裕度比实际非线性系统结果偏大，因此不能直接应用到非线性系统;此外，应该看到所求得的稳定裕度结果具有较小的保守性，说明文中的计算方法是可取的.更重要的是通过上述分析，给实际工程中稳定裕度的使用提供了可靠的保证.

5 结论

本文采用工程中的GDA为天线指向提供驱动力矩，在天线小角度机动条件下，针对两输入两输出的多体卫星线性控制系统，利用多变量频域理论中的序列回差设计技术，设计卫星本体俯仰姿态和天线指向控制器.另外重要的一点是，文中分析了整个控制系统的稳定裕度，分别利用计算量较小的回差阵奇异值法和逆回差阵奇异值法计算MIMO控制系统的稳定裕度，并把两者所求结果进行比较，得到系统稳定裕度保守性较小的最终结果.在此基础上，对所求稳定裕度结果进行了仿真验证，并得出一个重要结论:针对线性化后的线性MIMO系统分析得到的稳定裕度比实际非线性系统结果要偏大，这使得文中的稳定裕度分析更具有工程参考价值.

［1］ de GASTON R R E，SAFONOV M.Exact calculation of the multiloop stability margin［J］.IEEE Transactions on Automatic Control，1988，33(2):156-171.

［2］ DOYLE J.Analysis of feedback systems with structured uncertainties［J］.Control Theory and Applications，1982，129(6):242-250.

［3］ JUNG E S，ARUM S M，HANIPH A L.Robustness analysis for MIMO systems with unstructured uncertainties［C］//The 8thIEEE International Conference on Control and Automation.Xiamen，2010:1333-1337.

［4］ MUKHOPADHYAY V，NEWSOM J R.Application of matrix singular value properties for evaluating gain and phase margins of multiloop systems［R］.AIAA82-1573，420-428.

［5］ 李信栋，苟兴宇.MIMO线性定常系统稳定裕度的分析与改进［J］.控制理论与应用，2014，31(1):105-111.LI X D，GOU X Y.Analysis and improvement of stability margin for MIMO linear time invariant systems［J］.Control Theory＆Application，2014，31(1):105-111.

［6］ 苟兴宇，陈义庆，李铁寿，等.平台附件同时机动及其复合控制初探［J］.空间控制技术与应用，2009，35(5):1-5.GOU X Y，CHEN Y Q，LI T S，et al.Introduction to simultaneous maneuvers and composite control of spacecraft platform and its appendages［J］.Aerospace Control and Application，2009，35(5):1-5.

［7］ 曾海波.挠性多体卫星指向控制设计研究［D］.北京:北京控制工程研究所，2003.ZENG H B.Study on the design of flexible multibody satellite pointing control［D］.Beijing:Beijing Institute of Control Engineering，2003.

［8］ 白方周，庞国仲.多变量频域理论与设计技术［M］.北京:国防工业出版社，1988:331-340.