平均相对运动方程及其在卫星编队构型维持中的应用*

车汝才

(北京控制工程研究所，北京 100190)

O 引言

卫星编队飞行在空间领域具有重要的意义和应用前景，如实现对地立体观测、干涉测量、合成孔径雷达等.近年来国内外已有许多在轨工程应用，如美国TechSat-21编队飞行任务、欧洲的PRISMA编队飞行等任务［1］.在编队飞行的理论研究方面，许多学者进行了深入的研究并已取得了比较成熟的结论，例如以圆参考轨道为基础提出的C-W方程［2］，就有大量的研究成果和控制应用，针对椭圆参考轨道的 T-H 方程［3］及其解析解［4］，进一步扩展了应用的范围.近年来，学者们就如何进一步提高模型精度和实际应用作了很多探讨，如文献［5］在T-H方程中考虑J2项摄动从而提高计算精度，文献［6］则对T-H方程周期轨道进行了几何分析，另外也有学者用轨道根数来描述相对运动方程［7］.在编队飞行的构型控制中，文献［8］设计了数字滤波器来消除周期振荡从而减少燃耗，文献［9］则用C-W方程解的平均值进行构型控制.

虽然目前针对卫星编队飞行的理论研究比较成熟，但对其平均相对运动模型及其平均运动特性的研究相对较少，因此本文重点针对椭圆轨道卫星编队飞行的平均相对运动进行了研究，利用轨道周期平均化的思想推导了平均相对运动方程，并对平均相对运动特性做了定性分析.为分析方便，进一步推导了考虑摄动时平均相对运动的预报模型，该模型在短期内精度高，利用该模型可以在编队构型维持中提前预报出轨迹，为构型设计和规划提供参考依据.在此基础上设计了主动控制方式和被动控制方式两种不同的编队构型维持策略，并通过数学仿真进行了验证.

1 编队飞行的平均相对运动方程

首先定义如下坐标系:(1)地心惯性坐标系OXYZ:坐标系原点O为地心，X轴指向春分点，Z轴指向北极，Y轴按右手法则确定;(2)轨道坐标系oxyz:坐标系原点o位于参考星质心，x轴沿地心距方向，y轴在卫星的瞬时轨道平面内垂直于x轴，z轴按右手法则确定，如图1所示.

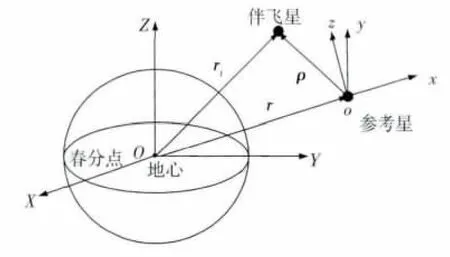
图1 坐标系示意图Fig.1 Illustrate of space coordinate

设参考星和伴飞星在地心惯性系中的位置矢量分别为r和rt，伴飞星相对于参考星的位置矢量ρ在参考星轨道坐标系中坐标为［x y z］T，则有

伴飞星与参考星的轨道根数差记为δσ=σt－σ.假设相对距离满足ρ≪r，相对位置与轨道根数差分之间的关系为［10］:

卫星在运行过程中，许多运动特性与轨道周期有关，也即相对位置呈现轨道周期性变化，如果能获取这些变化规律，将对相对运动轨道设计和构型控制具有一定的参考价值.受轨道根数周期项分析解的启发，本文采用平均化思想推导一个轨道周期内的相对运动方程.

利用级数展开式

以及不定积分公式

在二体问题下，δa，δe，δi，δω，δΩ 均为常值，对卫星相对运动方程在一个轨道周期内取平均值，以x轴的平均相对位置为例，推导中忽略e3以上的高阶项后近似有

同理可推导得出y轴和z轴的平均相对位置，最后整理可得

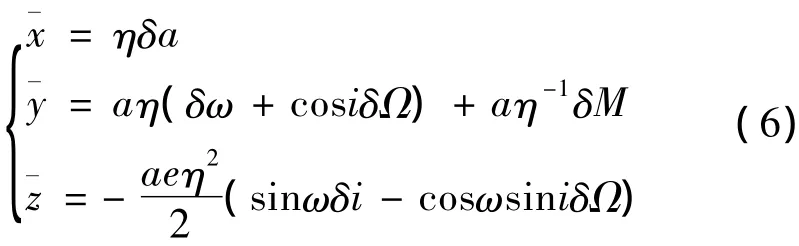
考虑摄动后轨道根数差分不再为常数，为消除轨道摄动影响，式(6)中取平均轨道根数，记平均轨道根数为，对应平均相对位置记为

2 平均相对运动轨迹的预报方程

2.1 预报方程的推导

利用式(7)可以实时计算平均相对位置，如果能提前预报出编队飞行的平均轨迹，将对构型设计和构型控制提供重要的参考信息，本节将利用轨道摄动模型，推导一种平均相对运动轨迹的快速预报模型.对于近地轨道卫星主要考虑J2项摄动和大气阻力摄动，根据相对运动的轨道摄动分析结论，轨道平均根数差分可表示为［11］

式中，K为面质比，δK为面质比差分.

S和G为相应的系数矩阵，

其中，

根据式(7)～(8)可得平均相对位置的预报方程

对于轨道平面内运动，在式(12)中消去时间后便得到航向与径向平均位置的关系式:

可以看出，面质比差分δK主要对平面内的相对运动产生影响，航向的长期变化近似为时间的二次函数;半长轴差分(t0)主要对径向和航向平均位置产生影响，对法向平均位置的影响较小，在构型设计和维持中可以通过合理选择δK和(t0)来控制平均相对位置的变化趋势.

2.2 仿真验证

下面通过数学仿真对前述平均相对运动方程的正确性加以验证，参考星和伴飞星初始轨道根数如表1所示，伴飞星与参考星的面质比差分为0.025 m2/kg，仿真时间约为32个轨道周期，仿真动力学模型中考虑J2项摄动和大气阻力摄动，图2给出真实相对位置曲线以及平均相对位置曲线，其中，实时平均轨迹对应式(7)，预报平均轨迹对应式(12).图3为预报平均轨迹的计算误差曲线.仿真结果表明，式(7)能够反映相对运动的平均特性，其变化规律与前面分析结果一致.预报方程(12)的计算结果与式(7)的计算结果基本吻合，模型线性化带来的预报误差在短期内基本可忽略.由于预报方程(12)具有计算简单、分析方便等特点，可事先预报出平均相对运动轨迹的变化趋势，因此可作为编队构型设计、构型规划与维持的参考.

表1 初始轨道参数Tab.1 Initial orbit elements

图2 真实相对轨迹与平均相对轨迹Fig.2 True relative track and averaged relative track

图3 预报平均轨迹的误差Fig.3 Error of forecast averaged relative track

3 基于平均相对运动方程的编队构型维持

(1)采用主动控制的编队构型维持

参考星和伴飞星初始轨道根数如表1所示，面质比差分δK=0.025 m2/kg，考虑设计余量取，根据式(13)可计算出伴飞构型保持所需的(t0)=12.67 m，根据式(12)可计算出(t0)=0.004°，进而利用平均根数与瞬时根数的转换关系，可以获得机动目标点的轨道根数，采用常规的双脉冲控制算法，限于篇幅，本文对具体控制算法不作详细说明.仿真时间为100个轨道周期，图4为主动控制方式的相对运动变化曲线，伴飞星编队构型维持所需速度增量为0.093 m/s.

(2)采用被动控制的编队构型维持

参考星和伴飞星初始面质比差分为δK=0.025 m2/kg，当伴飞星运行到时，通过调整伴飞星迎风面积，使得面质比差分为δK=－0.025 m2/kg;当伴飞星再运行到=0 m时，则将面质比差分调整为δK=0.025 m2/kg，利用轨道摄动特性实现编队构型的维持，仿真时间为100个轨道周期，图5为被动控制方式的相对运动变化曲线.

图4 主动控制方式的编队构型维持Fig.4 Initiative control of formation configuration maintaining

图5 被动控制方式的编队构型维持Fig.5 Passive control of formation configuration maintaining

4 结论

研究了平均相对运动方程及其在卫星编队构型维持中的应用，首先利用轨道周期平均化的思想，推导了轨道根数差分表示的平均相对运动方程，其次，利用轨道平均根数的线性化递推公式，给出了平均相对运动轨迹的预报方程，通过对平均相对运动轨迹的事先预报，为编队构型设计和维持提供了依据.最后通过数学仿真对两种不同的构型维持策略进行了验证.对于复杂的编队构型维持，如平面外构型维持、空间三维构型维持控制，后续还需要作进一步深入研究.

［1］ AMICO S D，ARDAENS J S.Spaceborne autonomous formation-flying experiment on the PRISMA mission［J］.Journal of Guidance，Control and Dynamics，2012，35(3):834-850.

［2］ COLHESSY W H，WILTSHIRE R S.Terminal guidance system for satellite rendezvous［J］.Journal for Aerospace Sciences，1960，27(9):653-658.

［3］ TSCHAUNER J F A，HEMPEL P R.Rendezvous zu einemin elliptischer bahn umlaufenden ziel［J］.Astronautica Acta，1965，11(2):104-109.

［4］ INALHAN G，TILLERSON M，HOW J P.Relative dynamics and control of spacecraft formations in eccentric orbits［J］.Journal of Guidance，Control and Dynamics，2002，25(1):48-59.

［5］ KATSUHIKO Y，MASAYA K.New state transition matrix for formation flying in J2-perturbed elliptic orbits［J］.Journal of Guidance，Control and Dynamics，2012，35(2):536-547.

［6］ MAI B，AKIRA I.Graphical generation of periodic orbits of Tschauner-Hempel equation［J］.Journal of Guidance，Control and Dynamics，2012，35(3):1002-1007.

［7］ SCHAUB H.Analytical mechanics of space systems［M］.Virginia:AIAA Education Series，2003.

［8］ VADALI S R，VADDI S S，ALFRIEND K T.An intelligent control concept for formation flying satellite［J］.International Journal of Robust and Nonlinear Control，2002，12(2/3):97-115.

［9］ BALAJI S K，ALFRED N.A bang-bang control approach to maneuver spacecraft in a formation with differential drag［R］.AIAA 2008-6469，2008.

［10］ SCHAUB H.Analytical mechanics of space systems［M］.Virginia:AIAA Education Series，2003.

［11］ 车汝才.跟踪空间非合作目标的轨道自主控制研究［D］.北京:中国空间技术研究院，2008.CHE R C.Research on orbit autonomous control for tracking a non-cooperative target in space［D］.Beijing:Chinese Academy of Space Technology，2008.