压电偏摆镜快速精确控制研究*

赵艳彬，许域菲，廖 鹤，刘 磊

(1.上海卫星工程研究所，上海 200240;2.大连理工大学，大连 116024)

O 引言

偏摆镜是部分空间光机系统的重要部件之一，如空间激光通信平台、空间光学望远镜、高分辨率侦查照相卫星等［1-7］.偏摆镜可以实现光束精确扫描镇定、光路调制以及光机抖振补偿，既可以实现对空间目标的精确捕获跟踪，也可以实现微弧度级指向.利用偏摆镜的扫描功能可以在小角度范围内对光机系统的光束进行扫描镇定操作.Masten［8］，Hilkert［9］和Gibson等［10］总结了航天器偏摆镜的精确扫描、光路调制和抖振补偿功能.

为实现偏转镜的快速精确控制，压电作动器或音圈作动器被广泛采用，但在实际应用过程中，由于受到作动器迟滞非线性和振动动力学的影响，仍然很难实现快速精确控制，开环误差可达驱动行程的10%～15%，当前的闭环控制精确跟踪的带宽常小于基频的1%，为提高控制带宽，各种控制算法被提出，如基于精确建模的逆模型补偿方法［11］，基于振动动力学的迭代学习补偿方法，基于神经网络的智能算法［12］等.但当前的反馈控制方法主要研究精确控制，而精确跟踪的带宽不够，并且这些算法需要建立系统较精确模型，计算复杂，在快速性方面仍需要进一步提高，不利于工程上大量推广.

为实现压电偏转镜的快速精确跟踪，本文设计一种前馈-反馈复合控制系统，在提高跟踪带宽的同时保证跟踪精度，并通过压电偏摆镜实验系统验证复合控制效果.本文提出的控制方法简洁有效，不需要辨识系统的精确模型，不但保证了快速精确跟踪性能，而且便于推广，适合应用在新一代的空间光机系统如激光通信平台、空间望远镜和侦查相机等.

1 压电偏摆镜系统

1.1 压电偏摆镜驱动原理

偏摆镜是现代光机系统的重要组成部分之一，图1表示偏摆镜的光束扫描功能示意图.

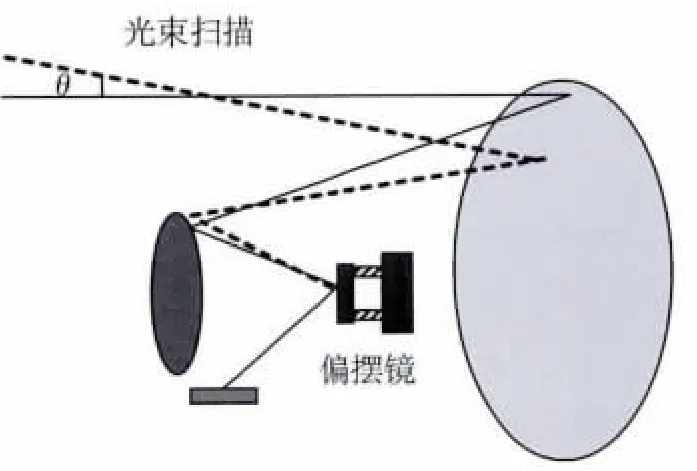
图1 偏摆镜进行光束扫描示意图Fig.1 Line of sight(LOS)scanning sketch of steering mirror

本文采用的压电偏摆镜驱动原理如图2所示，100 V恒压输入到压电堆栈I，通道CH1的控制电压u同时输入到压电堆栈I和II，压电堆栈I总输入电压为(100－u)，压电堆栈II的总输入电压为u，在控制电压u的驱动之下，压电堆栈I和II产生大小相等、方向相反的位移，而压电偏摆镜相应地产生偏转角θ.

实际工作时，需要考虑磁滞效应、蠕变效应和磁滞动力学影响，开环误差较大，很难满足快速精确扫描的要求，因此，本文将设计闭环控制系统.

为了实现闭环控制，需要测量压电偏摆镜偏转角.本文采用了一种间接测量的方法，即通过测量压电堆栈I和II的位移变化计算偏转角.由于压电堆栈作动器驱动位移小于15 μm，偏摆镜的偏转角小于0.1°，因此通过激光干涉仪进行校验，测量误差小于0.25%.

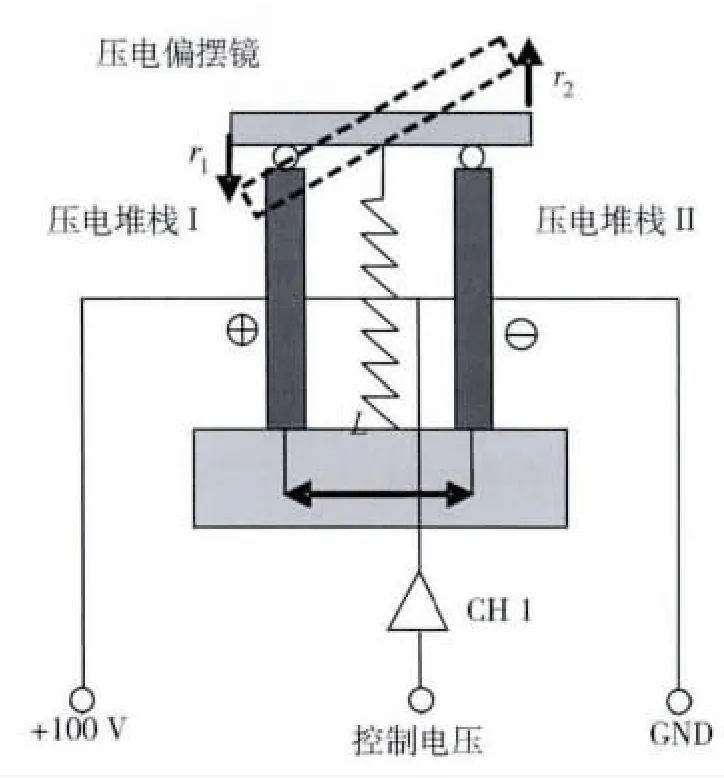
图2 偏摆镜进行光束扫描示意图Fig.2 Optical scanning of the steering mirror

1.2 压电偏摆镜实时控制系统

为实现压电偏摆镜的快速精确控制，本文搭建了基于实时仿真平台AD5435的半物理仿真系统.图3给出了压电偏摆镜进行闭环控制示意图，其中AD5435系统由16位数模DA卡、16位模数AD卡与AD5435控制卡组成.控制信号经电压放大器进行10倍放大，并采用位移传感器测量压电堆栈的微位移，进而给出偏转角，其中传感器信号的调制解调和电压放大器装配在一个机箱.

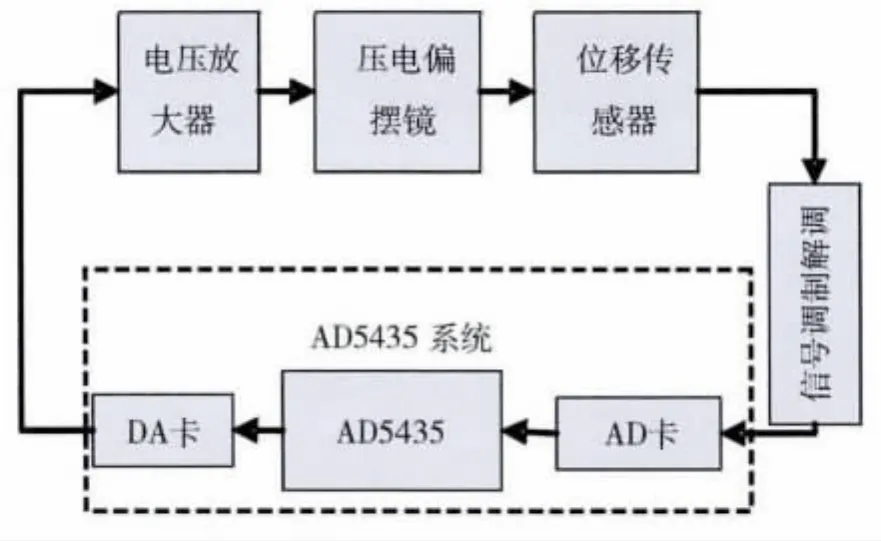
图3 偏摆镜闭环控制示意图Fig.3 Closed loop control sketch of the steering mirror

2 压电偏摆镜控制系统设计

2.1 压电偏摆镜系统动力学模型

压电驱动系统具有多场(机-电-热)耦合的特性［13-14］，并且动力学复杂包含迟滞效应、蠕变效应、机电动力学等［15-16］，如图4所示.压电系统迟滞动力学以及相关的辨识技术已经存在［15，17］，但是操作复杂，对使用者要求基础较高，本文将针对复杂迟滞动力学系统设计简洁有效的复合控制器.

图4 压电偏转镜动力学Fig.4 Dynamics of the steering mirror

迟滞效应是一种静态非线性效应，具有全局记忆效应，可采用如下的Preisach积分模型［18-19］

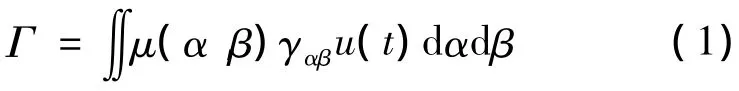
式中，μ(α，β)为密度函数，γαβ表示点(α，β)的切换值.

蠕变效应是一种低频效应，响应时间在分钟量级，可以采用如下模型描述［5］:

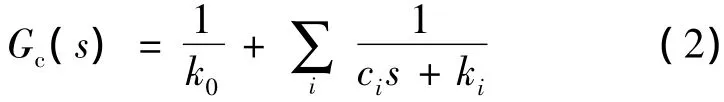
式中，k0为静态弹性系数.ci和ki是描述动态特性的阻尼和刚度.

压电系统的机电动力学(电阻电容和振动动力学)响应快，常以ms为单位，本文采用如下传递函数描述［15，17］:

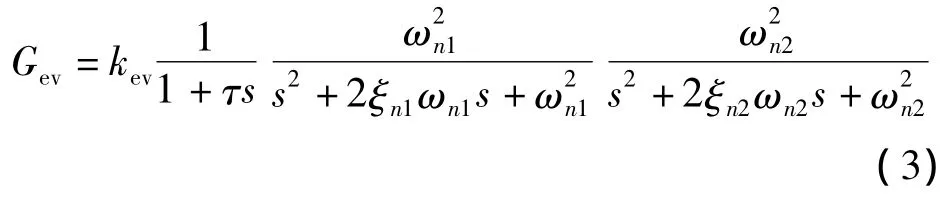
式中，kev为静态增益，τ为时间常数，本文考虑偏摆镜的二阶模态，ωn1和ξn1为一阶模态频率和阻尼，ωn2和ξn2为二阶模态频率和阻尼.

压电偏摆镜迟滞动力学是一种多尺度耦合动力学，并且各部分动力学时间尺度不一致，迟滞效应是一种非时间尺度非线性效应，蠕变效应是一种慢尺度效应，而机电动力学是一种快尺度效应，因此基于精确模型的控制比较复杂.

实验发现压电偏摆镜开环工作带宽高，可达kHz量级，但是由于受到磁滞效应、蠕变效应和机电动力学的影响，开环扫描跟踪精度不够，对极低频信号的开环跟踪误差仍可达10%，为实现快速精确控制，本文将研究前馈-反馈复合控制器.

2.2 反馈控制器设计

偏摆镜的反馈控制如图5所示，其包含滞后环节与陷波滤波.压电偏摆镜的开环带宽能够满足快速性要求，因此设计反馈控制时，采用滞后补偿控制器，不采用超前补偿控制器.滞后环节主要用来抑制蠕变效应和外部扰动，并补偿低频机电动力学.蠕变动力学主要集中在低频域，容易通过反馈抑制.

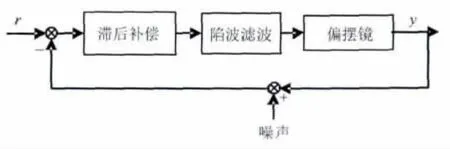
图5 偏摆镜反馈控制示意图Fig.5 Feedback control sketch of the steering mirror

滞后补偿环节

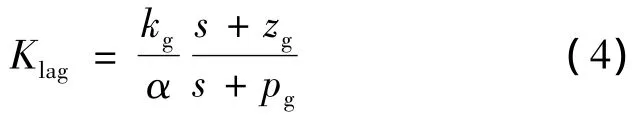
式中，zg是滞后环节零点，pg是滞后环节极点.α表示zg和pg之间比例系数，α计算如下:

式中，G表示非迟滞动力学，G=GcGev.

滞后环节的零点zg=ωc，滞后环节的极点pg可表示为

为提高系统的稳定性，设计陷波滤波器减小反馈控制器在系统180°相位处的增益.本文选择的两极点两零点陷波滤波如下:

式中，ζ0和ω0表示陷波器极点的阻尼和基频，和ω0表示零点的阻尼和基频.

2.3 复合控制器设计

反馈控制器设计时没有考虑静态迟滞效应，当跟踪谐波或三角波时，迟滞环节也会表现出类似的相位滞后，影响控制精度.为进一步提高跟踪速度，增加PD前馈用来补偿迟滞效应和部分机电动力学.前馈-反馈复合控制如图6所示.

图6 前馈反馈复合控制示意图Fig.6 Sketch of the feedforward-feedback composite control

3 压电偏摆镜控制实验

3.1 实验设备

压电偏摆镜实验系统包含主机、电压放大器、Strain Gauge传感器(SGS)、信号调制解调和AD5435系统，如图7所示.

图7 快速偏转镜跟踪实验Fig.7 Tracking experiment of the fast steering mirror

3.2 控制器参数

采用方波输入信号，估计非迟滞动力学，具体方法可见文献［15］，根据非迟滞机电动力学，选择穿越频率ωc=800π，α=3200，于是得到如下滞后补偿控制器:

根据实验中测量的迟滞曲线，并用相位滞后近似迟滞效应.为补偿滞后，PD前馈控制如下:

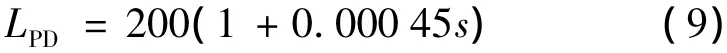
陷波滤波器的参数为ω0=500 Hz，=0.05，ζ0=0.3，得到如式(10)所示的陷波滤波器

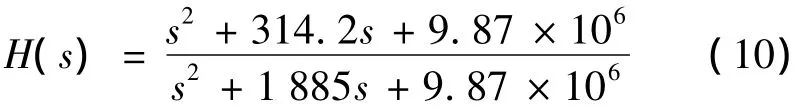
3.3 谐波跟踪

作为比较，首先采用整定的PID控制，50Hz谐波跟踪性能如图8所示，跟踪误差均方根2.3 μrad，相对均方根误差7.5%，采用前馈-反馈复合控制后跟踪性能如图9所示，跟踪误差均方根1.1 μrad，相对均方根误差3.6%，复合控制相对整定PID跟踪误差减小50%以上.

相对均方根误差如式(11)所示［20］:

式中，n是采样数，yr是参考角，y是输出角.

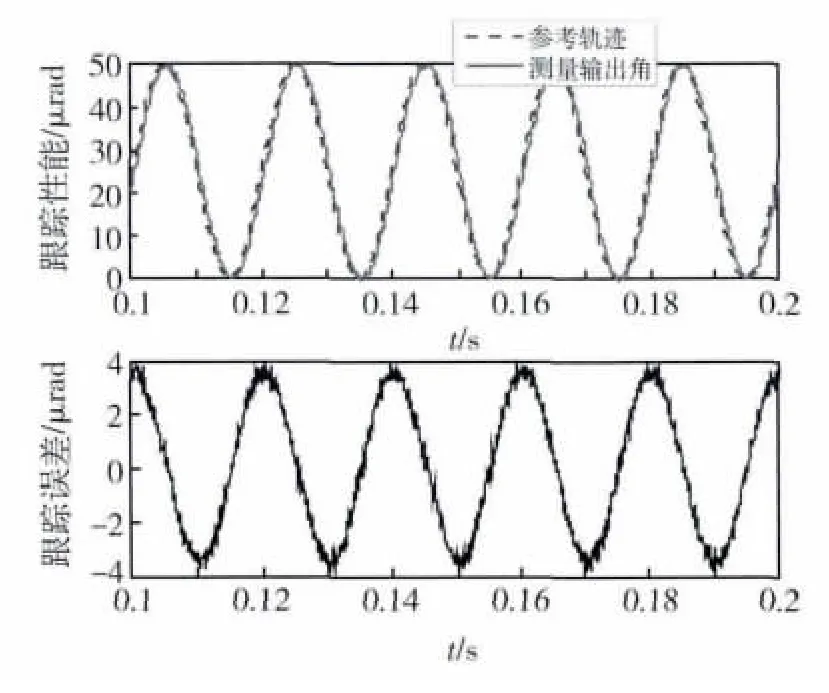
图8 谐波跟踪PID控制性能Fig.8 PID control performance of the sinusoidal signal tracking

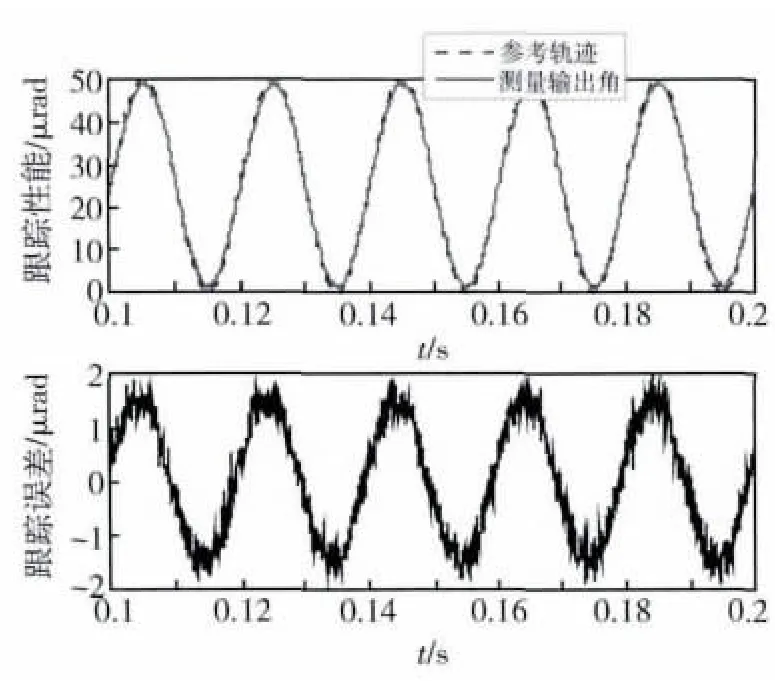
图9 谐波跟踪复合控制性能Fig.9 Composite control performance of the sinusoidal signal tracking

3.4 三角波跟踪

为进一步验证复合控制的跟踪性能，采用幅值50 μrad，基频50 Hz的三角波.当采用整定的PID反馈控制，跟踪误差均方根2.2 μrad，相对均方根误差7.66%，采用复合控制后，均方根误差 0.65 μrad，相对均方根误差2.26%，复合控制误差相对PID反馈控制误差减小70%以上.

最后采用复合控制对频带50 Hz具有随机特性的参考姿态角进行跟踪，如图12所示，跟踪误差均方根0.7 μrad，相对均方根误差2.1%，谐波、三角波和随机轨迹的跟踪实验证实了本文提出的前馈-反馈复合控制的有效性.

图10 三角波跟踪PID控制性能Fig.10 PID control performance of the triangle wave

图11 三角波跟踪复合控制性能Fig.11 Composite control performance of the triangle wave

4 结论

本文搭建并研究了压电偏摆镜的一种前馈-反馈复合控制系统，采用滞后补偿环节和陷波滤波进行反馈控制以及PD进行前馈控制.滞后环节用来补偿迟滞动力学、蠕变效应和外部扰动，PD前馈用来补偿迟滞效应，实验结果证实这种复合控制算法保证了压电偏摆镜的快速精确运动，本文提出的方法可以应用在高精光机系统的扫描跟踪、光路调制和抖振抑制等.

图12 随机参考跟踪信号(频带50 Hz)复合控制性能Fig.12 Composite control performance of the random reference signal with the bandwidth of 50 Hz

［1］ 韩诚山，李祥之，文明，等.基于压电偏转系统的卫星平台振动补偿［J］.光学精密工程，2011，19(9):2085-2091.HAN C S，LI X G，WEN M，et al.Vibration compensation of satellite platform based on piezo-electric steering system［J］.Optics and Precision Engineering，2011，19(9):2085-2091.

［2］ 黎明，黄勇.16 KM空间光通信的跟踪实验研究［J］.仪器仪表学报，2011，32(1):230-234.LI M，HUANG Y.Experimental study of tracking system for 16 km free-space optical communication［J］.Chinese Journal of Cientific Instrument，2011，32(1):230-234.

［3］ 李结安，谭久彬，崔继文.基于滤波的准直光束漂移反馈补偿方法研究［J］.光电子·激光，2013，24(2):336-342.LI J A，TAN J B，CUI J W.Study on method of feedback compensation drift of collimation beam based on filter［J］.Journal of Optoelectronics·Laser，2013，24(2):336-342.

［4］ 徐飞飞，纪明，赵创社.快速偏转反射镜研究现状及关键技术［J］.应用光学，2010，31(5):847-850.XU F F，JI M，ZHAO C S.Status of fast steering mirror［J］.Journal of Applied Optics，2010，31(5):847-850.

［5］ 谭立英，吴世臣，于思源，等.潜望式光通信终端反射镜安装误差补偿方法研究［J］.载人航天，2011，16(3):54-57.TAN L Y，WU S C，YU S Y，et al.Compensating algorithm of setting errors of reflex mirror in periscope intersatellite optical communication yerminal［J］.Manned Spaceflight，2011，16(3):54-57.

［6］ 吴松涛.导弹预警系统二维摆镜结构及其控制系统研究［D］.哈尔滨:哈尔滨工业大学，2006.WU S T.The study of the two-dimension waving mirror structures and the control system for early warning systems of the missile［D］.Harbin:Harbin Institute of Technology，2006.

［7］ 曲蔚然，林岩，刘洛霞.基于扫描反射镜的惯性稳像控制系统设计［J］.电光与控制，2013，20(9):69-73.QU W R，LIN Y，LIU L X.Design of an inertial image stabilization control system based on scan mirror［J］.E-lectronics Optics＆ Control，2013，20(9):69-73.

［8］ MASTEN M K.Inertially stabilized platform optical imaging systems:tracking dynamic target with mobile sensors［J］.IEEE Control Systems Magazine，2008，28(1):47-64.

［9］ HILKERT J M.Inertially stabilized platform technology:concepts and principles［J］.IEEE Control Systems Magazine，2008，12:26-46.

［10］ GIBSON S，TSAO T C，HERRICK D ，et al.Adaptive jitter control for tracker line of sight stabilization［C］//SPIE Conference on Advanced Wavefront Control:Methods，Devices，and Applications Ⅷ.San Diego:SPIE，2010:77-81.

［11］ CLAYTON G M，TIEN S，LEANG K K，et al.A review of feedforward control approaches in nanopositioning for high-speed SPM［J］.ASME Journal of Dynamics Systems and Control，2009，131(6):1-19.

［12］ LIAW H ，Shirinzadeh B.Neural network motion tracking control of piezo actuated flexure based mechanisms for micro nanomanipulation［J］.IEEE/ASME Transactions on Mechatronics，2009，14(5):517-527.

［13］ 蒋建平，李东旭.压电层合结构力学模型评述［J］.噪声与振动控制，2008，28(5):11-20.JIANG J P ，LI D X.Evaluation of modeling methods for piezoelectric laminate structures［J］.Noise and Vibration Control，2008，28(5):11-20.

［14］ JUHASZ L，MAAS J，BOROVAC B.Parameter identification and hysteresis compensation of embedded piezoelectric stack actuators［J］.Mechatronics，2011，21(1):329-338.

［15］ LIU L ，TAN K K ，TEO C S，et al.Development of an approach towards comprehensive identification of hysteretic dynamics in piezoelectric actuators［J］.IEEE Transactions on Control Systems Technology，2013，21(5):1834-1845.

［16］ LIU L，TAN K K，CHEN S L，et al.SVD-based preisach hysteresis identification and composite control of piezo actuators［J］.ISA Transactions，2012，51(3):430-438.

［17］ LIU L，TAN K K，LEE T H.Multirate-based composite controller design of piezoelectric actuators for high-bandwidth and precision tracking［J］.IEEE Transactions on Control Systems Technology，2013，99:1-1.

［18］ KRASNOSELSKII M A，POKROVSKII A V.Systems with hysteresis［M］.New York:Springer-Verlag，1989:22-23.

［19］ MAYERGOYZ I.Mathematical models of hysteresis［J］.IEEE Transactions on Magnetics，1986，22(5):603-608.

［20］ WU Y ，ZOU Q.Robust inversion-based 2-DOF control design for output tracking:piezoelectric-actuator example［J］.IEEE Transactions on Control Systems Technology，2009，17(5):1069-1082.