空间自锚式悬索桥体系转换吊索张拉力的确定

王建金 叶贵如

（浙江大学建筑工程学院 杭州 310058）

吊索张拉过程中，吊索力及相应吊索长度的准确计算是确保体系转换过程中主缆、主梁和主塔受力状态合理安全的重要保障，是指导吊索张拉施工的重要依据，也是对桥梁进行施工监控的重要工作.目前，国内许多学者对自锚式悬索桥的体系转换进行了深入研究，探讨了体系转换过程中吊索张拉顺序、张拉力的优化，以及对张拉过程中结构表现出的规律性进行研究，但是对于最基本的吊索张拉力和张拉长度的准确计算却没有给出一个通用而简便的计算方法［1－8］.

以江西上饶大桥为工程实例，研究体系转换过程中吊索拉力和吊索长度的计算方法，以及吊索张拉方案的优化，并对张拉过程中桥梁结构的受力状态进行分析.

1 等效节点力法确定吊索张拉力和长度

自锚式悬索桥体系转换过程中，主缆从空缆状态过渡到成桥状态.随着吊索的张拉，主缆发生大位移，主缆与吊索的连接点到吊索与主梁的锚固点之间的距离不断地缩短，吊索的一端固定，另一端的边界条件不断地发生变化［9－11］.

吊索张拉过程中，主缆和吊索的变化见图1.

图1 主缆张拉示意图

如图1所示，主缆从空缆状态1，经吊索张拉到达状态2和状态3，第一次张拉，吊索拉力为F1，吊索长度为L1，此时主缆已经发生较大位移，F1与L1根据主缆刚度和线形等的不同而成一定的关系，随着吊索力的增大，主缆由状态2变化到状态3，吊索长度也进一步缩短到L2.状态1到状态2再到状态3，主缆发生大位移变形，吊索长度和吊索拉力也随之发生较大的变化，整个变化过程表现出较强的非线性，给计算带来较大困难.如何准确计算各状态下吊索张拉力、吊索长度及主缆的受力和变形对于悬索桥体系转换的施工和监控有重要意义.

当前，存在许多桥梁设计方面的专业有限元计算软件，如 MIDAS，ANSYS，ABAQUS等，但是这些软件要准确模拟并计算出吊索张拉的整个过程却是比较困难的.

为了解决模拟主缆连接点到主梁锚固点之间的吊索长度不断变化很困难的问题，提出一种吊索张拉计算的方法：等效节点力法.

等效节点力法是将吊索对主缆的拉力等效为作用于吊索与主缆连接处（主缆索夹点）的节点力，在吊索与主梁的锚固处同样施加反方向的节点力.具体计算过程如下.

1）首先通过有限元计算软件迭代计算得到桥梁空缆状态的线形.

2）假定一组吊索拉力，换算出对主缆索夹点和主梁锚固点的等效节点力，并将相应的节点力作用于索夹点和锚固点.

如图2所示，当悬索桥的吊索面为竖直索面时，可以将吊索拉力等效为作用于主缆索夹点竖直向下的力F和主梁锚固点竖直向上的力F＋G，G为吊索的自重，因为吊索重量远小于其拉力F，因此G可忽略不计；当悬索桥的吊索面为倾斜索面（吊索顺桥向无倾斜，横桥向与铅垂线成一定的角度），忽略吊索自重，假定吊索拉力为F，在拉力F的作用下吊索在横桥向与铅垂线所成角度为θ，根据θ值，F可以分解为作用于主缆索夹点和主梁锚固点的竖直力F1和水平力F2.θ值介于吊索成桥角度和空缆状态锚固点，索夹点连线与铅垂线所成角度之间，因为主缆在张拉过程中索夹点位移不确定性，所以要精确确定θ值很困难.一般情况下经过F张拉后索夹点和锚固点之间的吊索长度已经较接近吊索成桥长度，θ近似地取为成桥角度.

图2 等效节点力示意图

3）在上述节点力的作用下对结构进行几何非线性分析，得到结构新的平衡状态，得到该状态下索夹点和锚固点之间的距离L（L1，L2，…，Ln），以及桥梁其他构件的受力状态.

4）判断L是否达到预期值，如果没有，修改吊索拉力（如Li大于预期值则应减小相应的吊索拉力值）重复过程2）和3）直到L达到预期的设定值.如图3所示，第i根吊索进行张拉，对主缆和吊索的受力状态进行计算时，假定一组F（F1，F2，…，Fi），在F 作用下计算得到L（L1，L2，…，Li）.吊索张拉后，吊索的无应力长度在后续吊索的张拉过程中将不会变化，所以为了满足吊索的这一特性，第i根吊索张拉时必需不断重复2）和3），更改F（F1，F2，…，Fi）的值，使前i－1根吊索的无应力长度保持不变，第i根吊索的长度达到预期的设定值.迭代的过程可以通过编制程序实现.

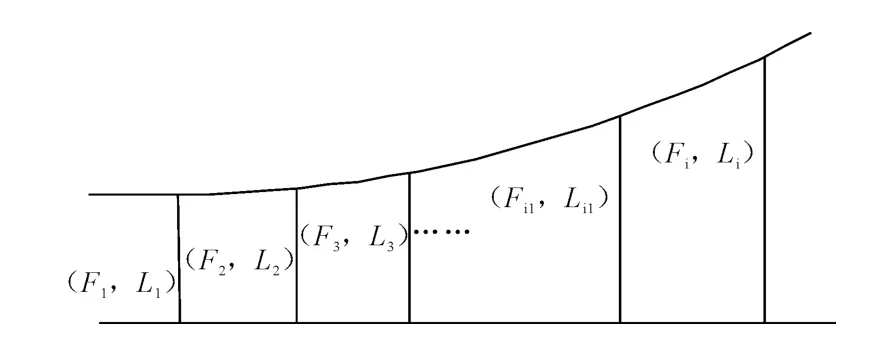
图3 吊索张拉示意图

5）经过2）和3）不断地循环迭代得到第i根吊索张拉后桥梁的平衡状态.分析主缆、主塔和钢箱梁的受力状态，主缆承受的拉应力不超过设计容许值，主梁的应力值控制在安全范围之内，主塔的偏位不超过设计给定的最大值，塔底不出现拉应力.若结构受力合理且满足施工安全，则计算得到的吊索张拉力和吊索长度可以指导施工，等效节点力法的计算框图见图4.

图4 等效节点力法示意框图

2 上饶大桥工程概况

江西上饶大桥是独塔空间自锚式悬索桥，桥梁跨径组合为60m＋50m＋158m.主塔采用钢筋混凝土结构，主梁为钢箱加劲梁，箱梁两侧各设2m吊索区.桥梁设2根主缆，主跨主缆采用三维空间线形，主跨吊索布置间距为9m，一共为14组.采用平行钢丝吊索，每个吊点设2根吊索.边跨主缆采用两根平行并排不加吊索的形式.由主塔处向箱梁锚碇处对吊索从DS1到DS14编号.桥梁采用先梁后缆的施工方法，钢箱梁架设完毕并进行压重后架设主缆，最后张拉吊索进行体系转换.结构立面及平面尺寸见图5.

图5 桥梁示意图（单位：cm）

3 体系转换方案优化

体系转换过程中，吊索力的准确计算是重中之重.吊索力的确定一方面要保证吊索在张拉过程中张拉力满足设计规定的安全系数，另一方面要考虑到现场施工条件、施工机具所能提供的吊索张拉力的限制.上饶大桥施工现场一共有4套张拉工装设备，上下游每侧吊索各2套，所以一侧吊索只能张拉2个索号.且考虑到施工安全性，1个索号的张拉力不能超过2 000kN.

运用结构计算软件MIDAS建立桥梁有限元模型进行空缆状态迭代计算，采用等效节点力法在主缆索夹点施加等效节点力对结构进行非线性分析.结果可知，对两侧吊索（近自锚端和近主塔端的吊索）1次张拉到位，张拉力小于2 000kN，满足结构和施工的安全性，对主梁跨中吊索如1次张拉到位，则吊索力将大于2 000kN，施工安全性得不到保障.所以部份吊索应分多次张拉到位.

确定张拉方案如下：体系转化分三轮完成.第一轮吊索张拉，先对其中张拉力较大的吊索进行初步张拉戴帽，拉力较小的吊索一次张拉到位；第二轮吊索张拉，将第一轮没有张拉到位的吊索张拉到成桥设计无应力长度.第三轮吊索张拉，桥面铺装完成后对吊索进行微调，使主缆和桥面线形达到设计值.

吊索由自锚端向主塔端进行张拉.经过计算可知主缆中部的吊索拉力较大，两端的拉力较小，所以拟定自锚端DS14～DS12和近主塔端DS2，DS11次张拉到位，跨中吊索DS11～DS3张拉戴帽.在张拉戴帽跨中DS8，DS7时，如果只在戴帽索前方设置1根辅助拉索的话戴帽索的拉力仍然很大，所以需要设置两根辅助拉索.因为施工方的张拉工装只有4套，只能同时进行1根吊索的张拉，所以若要设置两根辅助拉索，上下游两侧吊索分别需要3套工装.为了完成吊索的张拉，只能将其中的3套工装移到同一侧，另一侧只留1套.这样单侧张拉，一侧张拉完成后，移动工装进行另一侧的张拉.

假定塔顶主索鞍与主塔固结（实际情况下可能会发生滑移），两者共同变形，且暂不考虑主索鞍的顶推，塔顶主缆IP点纵向位置随体系转换过程推进不断发生变化，主塔的受力状态也随之发生变化.

图6与图7分别表示不考虑塔顶鞍座顶推主塔随施工推进塔底弯矩变化图，和主缆的应力在设计允许的安全范围内以及塔顶的纵向偏移量的变化曲线图.

图6 塔底在各工况下的弯矩图

图7 塔顶在各工况下的纵向偏移

可以看到，随着体系转换的进行，主塔的弯矩和偏位不断地增大，必须对主塔进行顶推，减小主塔受到的不平衡弯矩.桥面铺装完成后主缆IP点的最大纵向偏移量为43.2cm，由此可以确定主索鞍的预偏量，预偏量在施工过程中逐次顶回.因为设计规定体系转换施工过程中主塔纵桥向的最大偏位为9cm，所以吊索张拉时应该随时观测塔顶的偏移量，及时将主塔顶推到位.

第一轮张拉各吊索的张拉力和张拉长度及主塔的顶推见表1.

可以看到，跨中吊索张拉力较大，跨中向两侧张拉力逐渐减小.第一轮体系转换过程中吊索和主缆的应力在设计允许的安全范围内，满足规范和设计要求.主塔在施工过程中，不断地进行顶推，偏位始终控制在9cm以内，受力安全.

图8表示体系转换过程中，各个施工阶段的塔顶纵向偏移变化曲线.

图9为DS14～DS9吊索张拉过程中吊索力的变化曲线，可以得到以下结论：（1）初次张拉的索力值较大；（2）不考虑初次张拉的索力值，随着吊索张拉的进行，已张拉吊索的索力值平缓增加；（3）某根吊索张拉时，上一根吊索索力值大幅减小，与该张拉吊索相隔一根吊索的其他吊索索力值都会增加.

表1 体系转换施工步骤

图8 考虑顶推体系转换过程中塔顶纵向偏移

图9 DS14～DS9吊索力随吊索张拉变化曲线

以表1作为桥梁体系转换施工监控指令，施工完成后发现吊索张拉力和吊索长度理论计算值与具体的施工数值吻合较好，根据等效节点力法得到的桥梁监控数据很好地预测了桥梁的施工走向，使桥梁施工顺利地朝着既定的施工方向进行.

4 结束语

为了解决模拟与主缆连接点到与主梁锚固点之间的吊索长度不断变化较困难的问题，提出一种吊索张拉计算的方法，将吊索拉力等效为作用于主缆索夹点和吊索主梁锚固处的节点力.假定节点力的大小和方向，对结构进行几何非线性分析，不断地更改节点力的大小和方向，直到达到预期的吊索长度.在指定节点力的作用下可以准确计算出桥梁的受力状态，对桥梁施工进行监控.

将等效节点力法运用于江西上饶大桥的施工监控计算，计算结果很好地预测了结构的施工动向，等效节点力法具有可行性.

［1］胡建华，沈锐利，张贵明，等.佛山平胜大桥全桥模型试验研究［J］.木工程学报，2007（5）：17－25.

［2］唐 启，李传习，柯红军.独塔双跨空间索面自锚式悬索桥体系转换方案确定［J］.公路交通技术，2010（1）：73－77.

［3］柯红军.广州猎德大桥体系转换施工方法的确定及实施［J］.桥梁建设，2010（2）：80－83.

［4］张玉平，董创文.江东大桥双塔单跨空间主缆自锚式悬索桥的施工控制［J］.公路交通科技，2010（7）：76－82.

［5］胡建华.现代自锚式悬索桥理论与应用［M］.北京：人民交通出版社，2008.

［6］张俊平，黄海云，刘爱荣，等.空间缆索自锚式悬索桥体系转换过程中受力行为的全桥模型试验研究［J］.土木工程学报，2011（2）：109－115.

［7］孙全胜，高红帅.空间主索自锚式悬索桥体系转换施工控制［J］.中外公路，2013，33（2）：112－116.

［8］冯 钢，邓 武.湘江三汊矶大桥主孔自锚式悬索系统安装及体系转换［J］.公路工程，2008，33（4）：110－113.

［9］张建东，赏锦国，黄元群.自锚式悬索桥吊杆安装及体系转换新技术［J］.公路，2010（5）：7－11.

［10］杨继承，卢 颖.自锚式悬索桥吊索张拉无应力状态仿真分析方法［J］.公路交通技术，2013（3）：100－104.

［11］黄海云，张俊平，刘爱荣，等.自锚式悬索桥吊索张拉过程中索力变化规律的试验研究［J］.铁道建筑，2010（4）：10－13.