基于ANSYS的悬索桥主缆优化找形计算方法

吴章旭

(广西交通职业技术学院，广西 南宁 530000)

0 引言

悬索桥主要是由主缆、吊索、主塔和锚固系统组成，在成桥状态下桥面荷载由吊杆弹性支撑，吊索以集中荷载的形式将荷载传递给主缆，主缆再将轴力传递给主塔支撑结构与锚固系统。主缆线形是由节点作用下的平衡状态决定，主缆线形计算的精确理论有分段悬链线法[1]、虚拟梁法[2]，这两种方法均有解析公式可以进行解析迭代找形。文章通过对悬索桥主缆系统模型进行简化分析，在满足其几何边界条件与荷载平衡条件下，采用有限元建模进行迭代计算的主缆找形计算。

1 初拟计算参数

提出有限分析迭代方法为简化模型只对中跨主缆进行分析，首先假设主缆初始参数：直径为0.2 m，中跨跨径100 m，矢跨比为1/5，两理论IP点所在高程均为20 m。靠近塔柱处的吊杆间距为10 m，其余吊杆间距为8 m，全桥共计11根吊杆。

主缆线形的分段悬链线与抛物线的线形比较近似，因此采用满足两个IP点坐标以及主缆最低点坐标约束的几何边界条件，建立主缆找形的初始构形由式(1)确定主缆节点坐标。

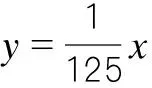
(1)

靠近塔柱处的主缆吊点受到1 200 kN的集中荷载作用，其余主缆吊点受到1 000 kN的集中荷载作用，主缆建模初始线形如图1所示。

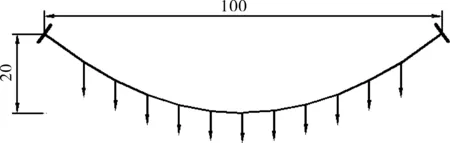
图1 主缆初始建模线形图

2 有限元模型分析

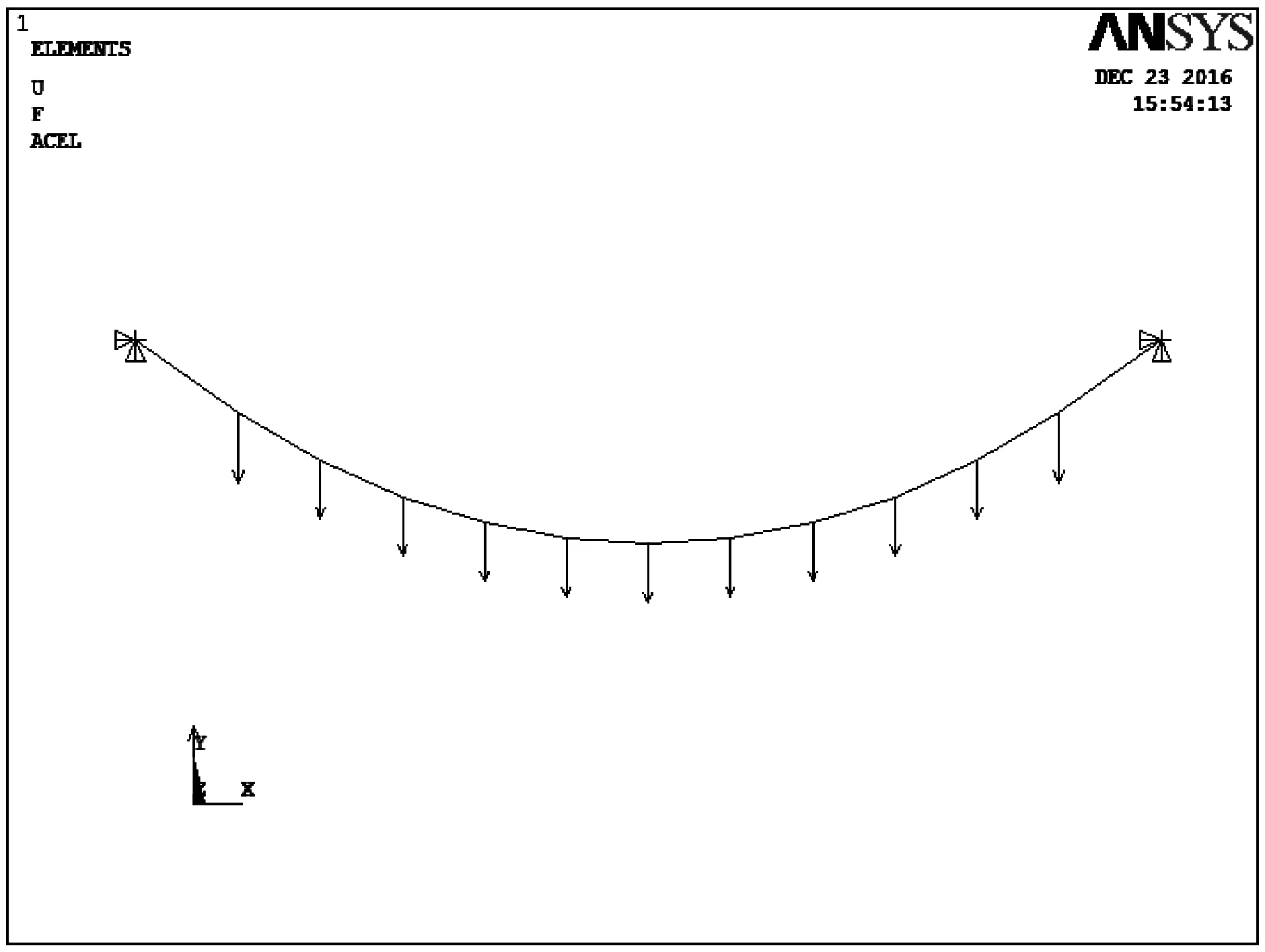
图2 缆索找形初始有限元模型图

直接建立有限元模型，主缆吊点之间采用一个单元连接，等效为文献[3]介绍的节线法，首先在吊点所在的里程上建立节点，然后用只受拉的Link10单元连接成主缆初始线形，最后施加吊索处节点荷载，如图2所示。

2.1 迭代计算原理

采用直线单元模拟分段主缆之间的悬链线分析主缆的成桥线形具有较高的精度，每一段主缆在平衡状态下有不同的初始应变。可采取两种分析思路进行主缆优化找形：

(1)每段主缆分别赋予初始应变，均作为设计变量进行优化；(2)每一跨的分段主缆均赋予统一的初始应变，每一跨只有一个设计变量。

由于初始建模的抛物线线形并不是主缆平衡状态下的线形，主缆节点均会产生位移而达到平衡状态，而且采用两种初值赋予的方法求解主缆线形，会得到相同的计算结果，因此采用第二种方法可以很大程度减少设计变量的数量，减小优化找形的计算量，减少程序运行时间。

设计给出的成桥状态为了保证吊杆在纵桥向不发生倾斜，因此吊杆在纵桥向位置坐标是固定不变的，而初始以抛物线建模时就已经将主缆节点建立在了实际成桥位置，在赋予初始应变的主缆的平衡状态求解分析时，主缆节点必定会产生纵桥向的位移，而不满足设计的边界条件。因此在第一次求解的基础上获得主缆节点的纵向位移，再将此位移反向叠加到初始建模的主缆的纵向坐标上，再次优化分析方法对主缆进行找形，即能得到满足设计边界条件的主缆成桥线形。

2.2 设计变量初值

选择一个合适的主缆初始应变，可以加快程序的收敛。因此可以根据经验进行赋值，也可通过试算确定，同样也可采用抛物线主缆线形计算理论近似计算初始应变，见式(2)和式(3)。

(2)

(3)

2.3 一次优化结果

采用初始参数进行优化分析获得主缆平衡状态下的节点坐标，见下页表1。

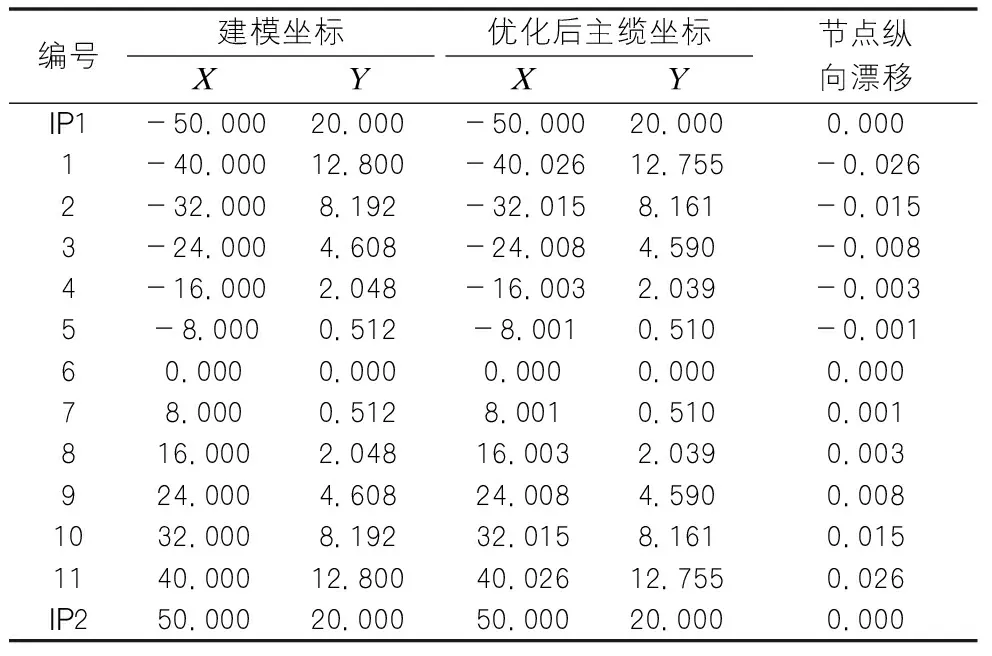
表1 优化结果主缆节点坐标表

从优化计算结果分析可以看出主缆节点在纵桥向发生了厘米级偏移，这样的偏移量不可容忍，因此需要进一步迭代分析。将主缆建模初始节点坐标位置，按纵向位移反号进行叠加，见式(4)。

X1=X0-Ux(i)

(4)

式中：X1——迭代计算主缆节点纵向坐标；X0——主缆节点初纵向初始坐标；Ux(i)——上一次主缆节点纵向位移值。

2.4 迭代分析计算

由式(4)求得新的主缆节点纵向坐标后，再由式(1)计算求得主缆节点竖向坐标，从而获得更新后的主缆节点建模坐标，采用相同的优化求解程序进行求解。获得平衡状态下主缆节点坐标，见表2。

从表2中数据分析，经过一次迭代后的优化求解结果可以看出主缆节点的最大偏移量只有1 mm，求解结果已经达到很高的计算精度。

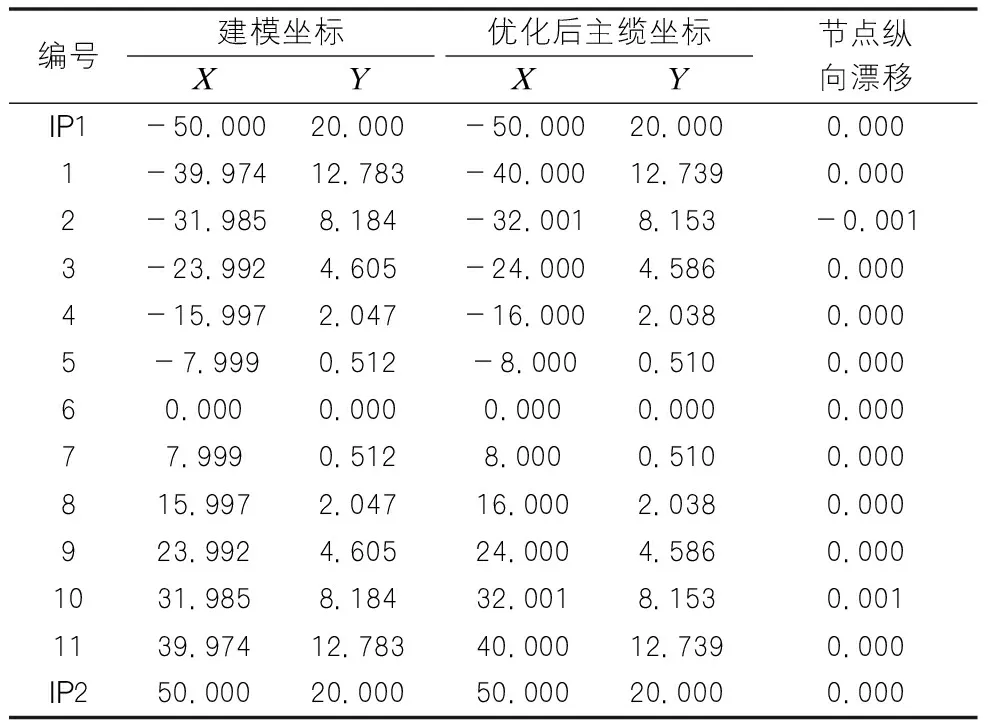
表2 迭代优化结果主缆节点坐标表

2.5 主缆无应力长度提取

优化求解结束后找到了一组满足一系列边界条件和目标函数最小的设计变量，通过后处理更新主缆节点坐标(UPCOORD，1)就可直接提取节点坐标值，得到主缆的成桥线形。节点更新后的单元长度即为主缆的分段有应力索长Si，同时可以提取单元总的弹性应变εi。由于Link10单元是线性应变单元，其弹性伸长梁的计算是相对于初始建模时的单元长度，即更新节点前的单元长度Li。因此主缆单元的分段无应力长度公式见式(5)。

S0i=Si-Liεi

(5)

式中：S0i——主缆分段无应力索长；Si——主缆分段有应力索长；Li——更新节点前主缆分段几何长度；εi——主缆分段应变。

3 分析结果验证

采用优化算法进行主缆找形分析，节点纵桥向位置以及主缆矢跨比均满足设计要求。采用分段弹性悬链线法计算主缆节点竖向坐标，以及分段无应力索长，同迭代求解后主缆线形的优化分析结果进行对比，见表3。

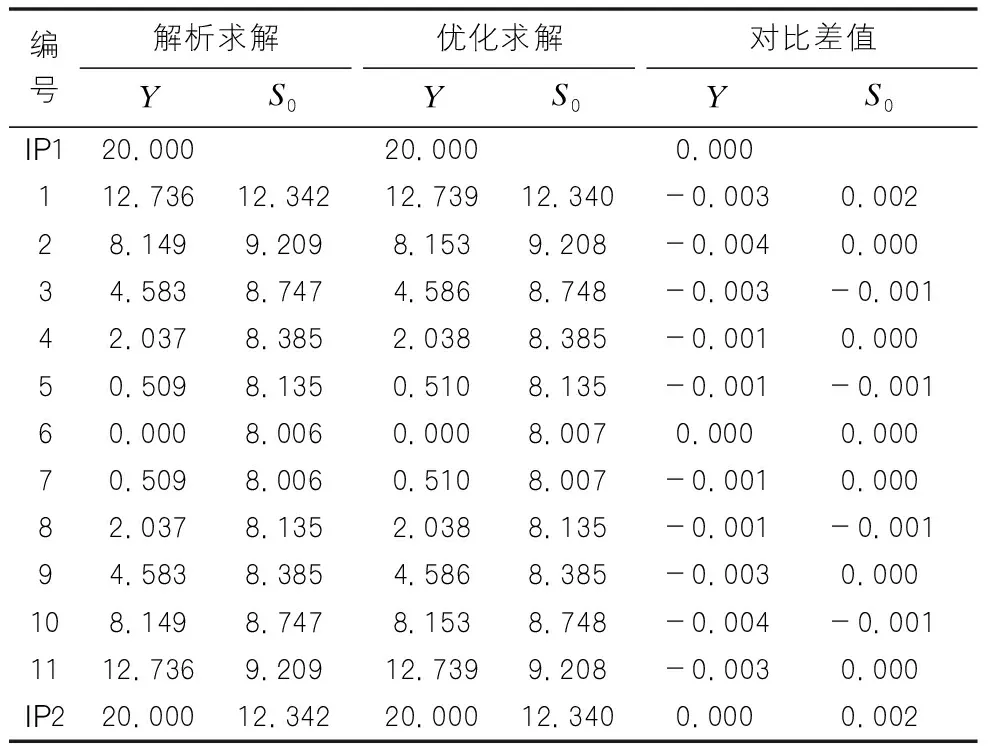
表3 优化找形结果验算表

从表3中，采用精确的弹性悬链线法对主缆找形，同迭代优化算法对主缆找形对比分析，可知主缆分段无应力索长只有细微的差别，因此可以说明迭代优化算法对悬索桥主缆进行找形的正确性，其中分段无应力索长几毫米的差别是因为有限元计算时主缆分段节点之间是采用一个直线单元连接，而解析方法计算时主缆分段节点之间为悬链线，这种差异会随着主缆轴向应力的增大而消除。

4 结语

采用ANSYS优化模块对集中荷载作用下的悬索桥主缆进行找形分析，是抛开了主缆线形求解的理论解析公式进行计算分析，能够在有限元计算平台上独立实现。若要计算三跨主缆模型只需要在中跨模型的基础上，分别赋予两个边跨初始应变，并约束IP点处的不平衡力大小限值，采用相同的优化迭代方法即能够对受集中荷载作用下的三跨主缆进行找形分析。

[1]唐茂林.大跨度悬索桥空间几何非线性分析与软件开发[D].成都：西南交通大学，2003.

[2]肖汝诚，贾丽君，王小同.确定大跨径悬索桥主缆成桥线形的虚拟梁法[J].计算力学学报，1999(1)：108-114.

[3]Kim h k，Lee m j，Chang s p.Non-Linear Shape-Finding Analysis of a Self-Anchored Suspension Bridge[J].Engineering Structures，2002，24(12)：1547-1559.