大跨悬索桥吊索阻尼比影响因素分析

李胜利，张 帅，王东炜，欧进萍

(1. 郑州大学 土木工程学院，郑州 450001；2. 哈尔滨工业大学 土木工程学院，哈尔滨 150090)

大跨悬索桥吊索阻尼比影响因素分析

李胜利1，张 帅1，王东炜1，欧进萍2

(1. 郑州大学 土木工程学院，郑州 450001；2. 哈尔滨工业大学 土木工程学院，哈尔滨 150090)

确定大跨悬索桥吊索的阻尼比及其影响因素是设计中的难点，且目前吊索流固耦合二维数值计算中吊索阻尼比取值的实际工程意义不太明确，为了利用二维流固耦合计算实际工程中吊索的风振特性，其中吊索断面刚度和阻尼的取值至关重要，为了研究吊索断面的阻尼特性，采用自由振动衰减法和有限元方法分析了吊索初始张力、长度、直径、风速、约束条件以及吊索位置对吊索阻尼比的影响。结果表明：吊索阻尼比随其初始张力的增大而增大，吊索阻尼比随其直径和长度的增大而减小；吊索阻尼比随风速的变化而变化；吊索两端为固定端约束时的阻尼比大于吊索两端为固定铰约束时的阻尼比；吊索的跨中阻尼比最小，从跨中向两端吊索阻尼比逐渐增大。因此在吊索流固耦合计算时，吊索阻尼比的取值随吊索初始张力、长度、直径、风速、约束条件以及吊索位置的不同而不同。

悬索桥；吊索；自由振动；位移时程；阻尼比；有限元法；流固耦合

阻尼比在结构故障诊断、振动实时监控、荷载识别、噪声控制及动力响应等研究中有重要意义[1-2]；但阻尼比的识别精度一直不高，受测量方法影响较大，提高阻尼比识别精度成为主要研究目标[3-4]。悬索桥的主要传力构件是索，索是一种柔性构件，刚度、质量和阻尼相对较小，特别是吊索容易在各种激励下发生振动，影响桥梁的结构安全和使用寿命[5]。近年来已建成的大跨度桥梁，如我国的西堠门大桥、丹麦的Great Belt桥东引桥、英国的Second Severn桥、巴西的Rio-Niteroi桥、日本东京湾桥、加拿大Lion Gate桥等都出现过吊索的涡激振动，因此吊索涡振是桥梁风工程领域中一个非常重要的问题[6]。由于三维流固耦合模拟技术的复杂性，Al-Jamal等[7-10]对涡激振动开展了二维数值研究。因为吊索阻尼比受初张力、直径、长度、约束情况、风速以及吊索位置的影响，所以二维数值计算中阻尼比取值与实际脱节，因此，吊索阻尼比影响因素分析对吊索流固耦合二维数值计算能否与实际工程相结合具有极其重要的意义。

阻尼比的测定和识别方法主要有自由振动衰减法、共振法、脉动法、傅氏变换法等，所有这些方法，所依据的都是线性弹性振动理论[11-14]。Newmark等[15]根据他们对原型和模型的实测数据，建议按不同结构和不同内力等级采用不同的阻尼比；梁超锋等[16]分析了材料阻尼对结构阻尼比影响，得到了材料损耗因子与结构模态阻尼比之间的关系；赵晓丹等用快速傅里叶变换加连续傅里叶变换推导衰减系数计算公式，利用分段积分分列方程识别阻尼比；陈奎孚等[17]采用理论分析与数值仿真相结合的方法构造了半功率带宽法估计阻尼比。迄今为止，还没有一种大家所共同接受的、行之有效的获取结构阻尼特性的方法。

本文利用有限元软件ANSYS分别采用link单元和beam单元建立以吊索跨中冲击荷载为理想激励源的吊索参数振动模型，分析成桥状态下吊索在跨中激励下的位移时程特性，采用自由振动衰减法计算吊索的真实阻尼比。最后以某悬索桥吊索为工程背景，在验证分析方法可靠性的基础上，分析吊索阻尼比算法的准确性，讨论了吊索初始张力、直径、长度、约束情况、风速和吊索位置等因素对吊索阻尼比的影响。

1 计算方法及工况的确定

1.1 计算方法

吊索承受水平方向风荷载和冲击荷载作用的示意图如图1(a)所示，其中，Q1为吊索底部风荷载，Q1+Q2为吊索顶端风荷载，F为吊索竖直方向张力，L为吊索长度，E为吊索弹性模量，I为截面惯性矩。根据自由振动衰减理论，阻尼比 与振幅A的关系如式(1)所示[18]。

(1)

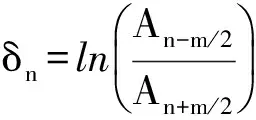
图1 自由振动衰减法示意图Fig.1 The schematic diagram of free damped vibration

自由振动衰减法将吊索任意位置自由衰减看做单

自由度体系自由振动[19]，根据式(1)并结合吊索目标变形计算吊索阻尼比。其计算过程为：①使用有限元软件建立吊索在风荷载作用下的有限元模型；②对吊索施加一个持续两个自振周期的正弦荷载N如式(2)，计算吊索自由振动衰减时程如图1(b)；③将吊索振幅值带入式(1)，计算不同影响因素下吊索阻尼比。

N=1×104sin(2πfnt)

(2)

式中：fn为吊索第n阶自振频率；t为正弦荷载持续时间。

本文选取矮寨悬索桥与钢桁梁链接的最长吊索J01进行验证，该吊索在成桥状态下的结构参数如表1所示，计算结果如表2所示，本文的计算结果在误差允许的范围内，表明了本文计算模型和方法的正确性。

表1 验证选取吊索的基本参数

表2 计算结果

1.2 计算工况

本文以西堠门大跨悬索桥的吊索为例进行研究。西堠门大桥位于浙江省舟山市，是舟山大陆连岛工程中的一座超大跨径桥梁，主桥为两跨连续半漂浮钢箱梁悬索桥。主桥的跨径组合为1 650 m+578 m，桥面宽36 m，塔高211 m，主缆矢高为165 m，矢跨比为1/10，全桥的纵坡为2.5%。主缆1 770 MPa高强镀锌平行钢丝，吊索采用三种规格，公称直径分别为60 mm、80 mm和88 mm的高强镀锌钢芯钢丝绳，其公称抗拉强度分别达到了1 770 MPa、1 860 MPa和1 960 MPa，与主缆连接形成了吊索，索夹左、右分半[21]。吊索与箱梁锚箱采用销铰连接，吊索最短长度为4.552 m，最长长度为169.819 m，吊索标准间距为18 m。大桥吊索构造如图2所示，吊索布置立面图如图3所示。本文计算中假定骑跨式吊索四根索股受载荷情况一致且相互独立，因此理论和有限元计算中仅取一根索股为研究对象。

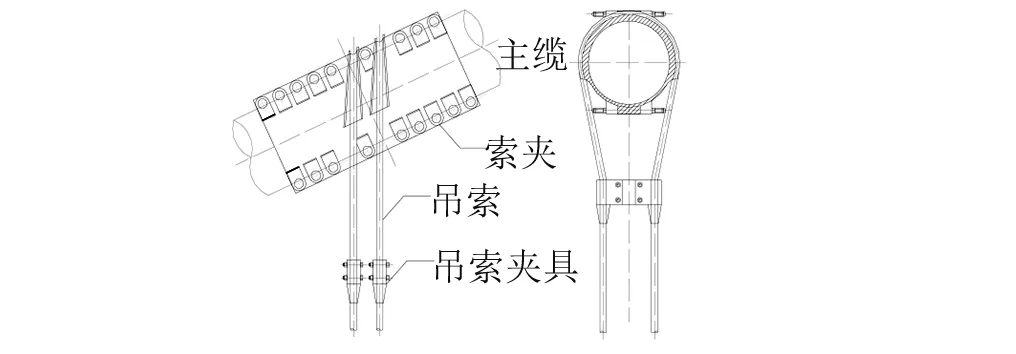
图2 吊索构造Fig.2 The structure of sling

图3 西堠门大桥吊索布置立面图Fig.3 The elevation of sling in xihoumen bridge

本文以西堠门大桥实际尺寸建立吊索模型，分别采用beam单元和link单元建立有限元模型如图4和图5所示，选取中跨#46号、#54号、#57号、#60号、#65号以及#70号吊索如图3所示为计算工况，在顺桥向风作用下吊索单位长度上的风荷载按式(3)计算

(3)

式中：ρ为空气密度，kg/m3，取1.25；CH为悬索桥的阻力系数在考虑与活载组合时，取1.0，在设计基准风速下可取0.8；α为地面粗糙度系数；D为吊索的直径，m；GV为静阵风系数；Vs10为桥址处的设计风速，即地面或水面以上10m高度处，100年重现期的10min平均年最大风速，m/s。

图4 吊索beam单元有限元模型Fig.4 The beam unit finite elements model of sling

图5 吊索link单元有限元模型Fig.5 The link unit finite elements model of sling

2 吊索阻尼比影响参数分析

2.1 吊索张力的影响

由于吊索是在架设完加劲梁和主缆后安装并张拉的，所以吊索张力的大小对悬索桥的内力状态影响很大。本文选取西堠门大桥中跨如图3所示的#46号、#54号、#57号和#60号吊索，以吊索张力设计值F=390.2kN为基数，计算张力为F/3、F/2、F、2F和3F，其他参数保持不变，建立计算模型，并分析比较计算结果，吊索的基本参数如表3示。有限元计算吊索在不同张力的情况下的跨中阻尼比如图6所示，由图可见，当初张力增大时，吊索的跨中阻尼比均呈增大趋势；吊索的长度越短，其阻尼比越大；吊索阻尼比增长的斜率随吊索长度的增大而迅速减小，随着吊索长度的增加，吊索跨中阻尼比越来越接近。

表3 吊索的基本参数

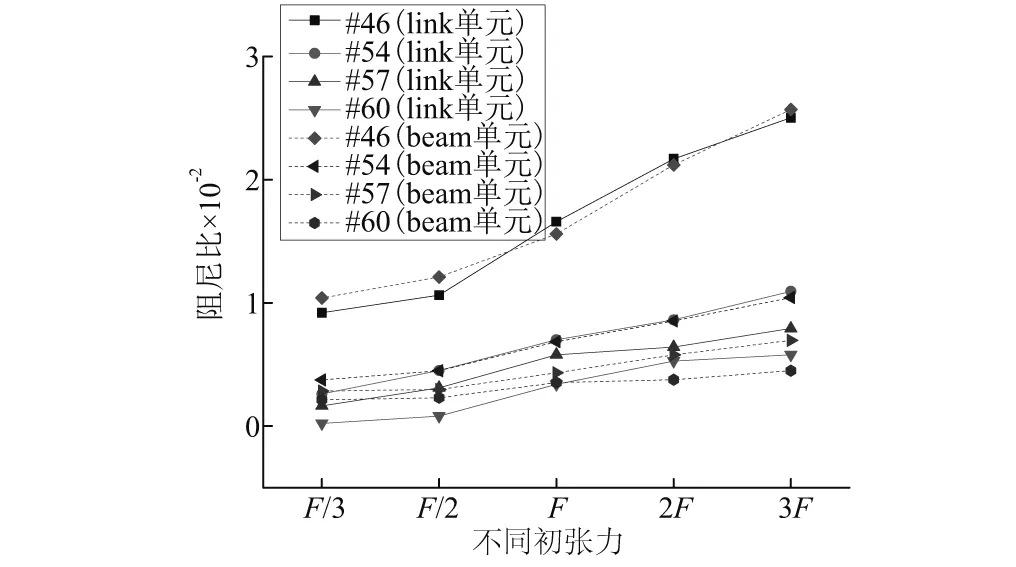
图6 不同初张力吊索跨中阻尼比比较Fig.6 The comparison of different initial tension sling span damping ratio

2.2 吊索直径的影响

为研究吊索直径对吊索阻尼比的影响，本文选取西堠门大桥中跨#54号、#57号、#60号和#65号吊索为研究对象，选取设计直径D=0.06 m为基数，计算直径为D/3、D/2、D、2D、3D时每根吊索的阻尼比，吊索参数取值如表4所示，本文有限元方法计算结果如图7所示。

表4 吊索的基本参数

图7 不同直径吊索跨中阻尼比比较Fig.7 The comparison of damping ratio of different diameter sling

由图7可知，#54号、#57号、#60号以及#65号吊索的阻尼比均随着吊索直径的增大而减小；而吊索长度越短减小趋势越明显，吊索长度越长，吊索阻尼比减小趋势越不明显。

2.3 吊索长度的影响

由于吊索的长度差距很大，最长的吊索为169.82 m，最短的吊索为4.55 m，所以吊索的长度对吊索阻尼比的影响很大。本研究选取西堠门大桥中跨#46号、#54号、#57号、#60号、#65号、#70号和#75号吊索，吊索长度从4.56 m逐渐增加到76.76 m，而吊索直径、初张力、弹性模量、风荷载等参数取值见表5所示。有限元计算吊索在不同长度下的跨中阻尼比如图8所示。由图7可见，当其它因素不变时，随着吊索长度的增加，吊索跨中刚度呈逐步下降的趋势。

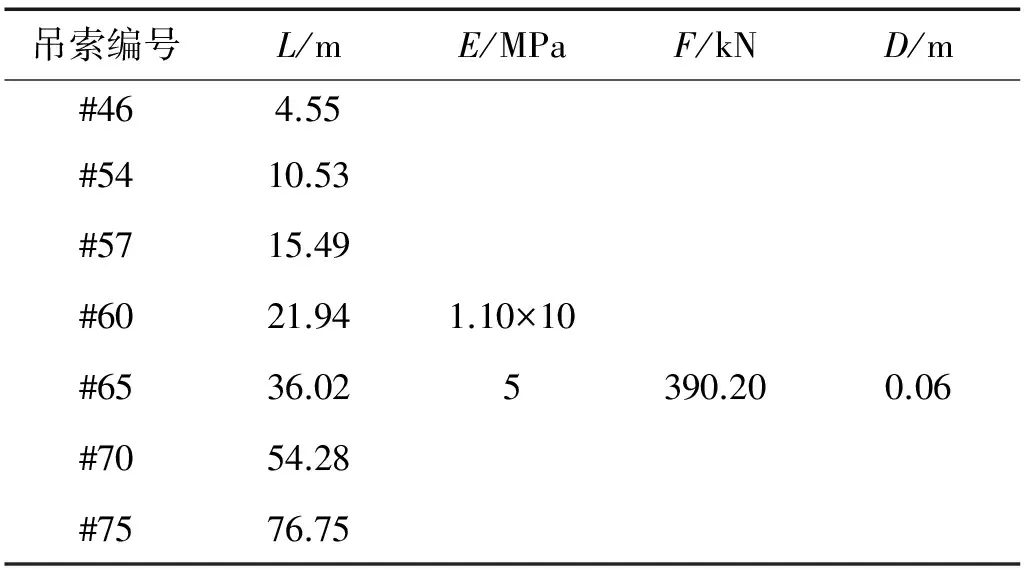
表5 吊索的基本参数

图8 不同长度下吊索的阻尼比Fig.8 The comparison of damping ratio of different length sling

2.4 风速大小的影响

本文选取#46号、#54号、#57号和#60号，风速分别取0 m/s、10 m/s、20 m/s、30 m/s、40 m/s。吊索的基本参数如表6所示，吊索有限元计算吊索跨中阻尼比如图9所示。由图9可见，随着风速的增大，吊索阻尼比呈减小趋势；不同吊索在同一风速下阻尼比不同，同一吊索在不同风速下阻尼比也不同。

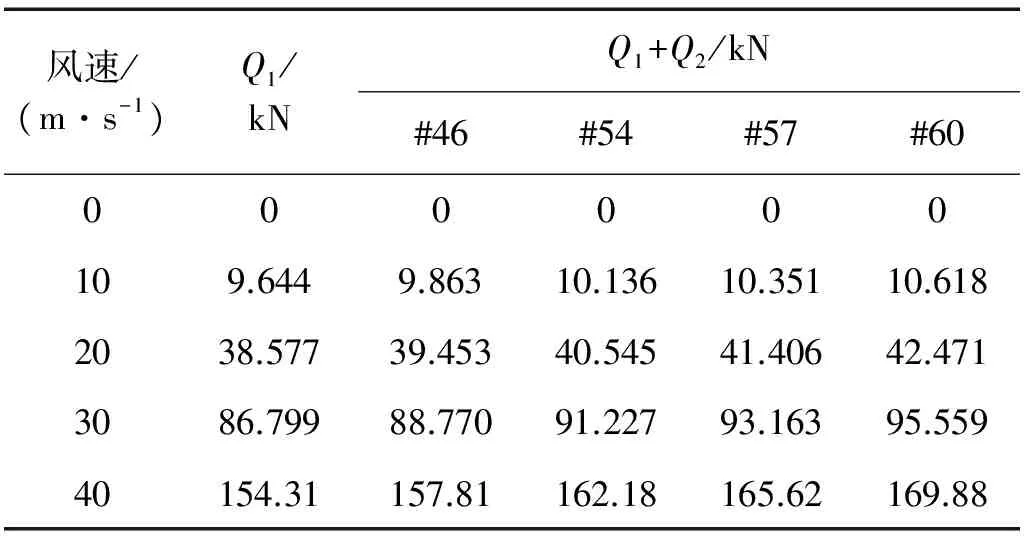
表6 吊索的基本参数

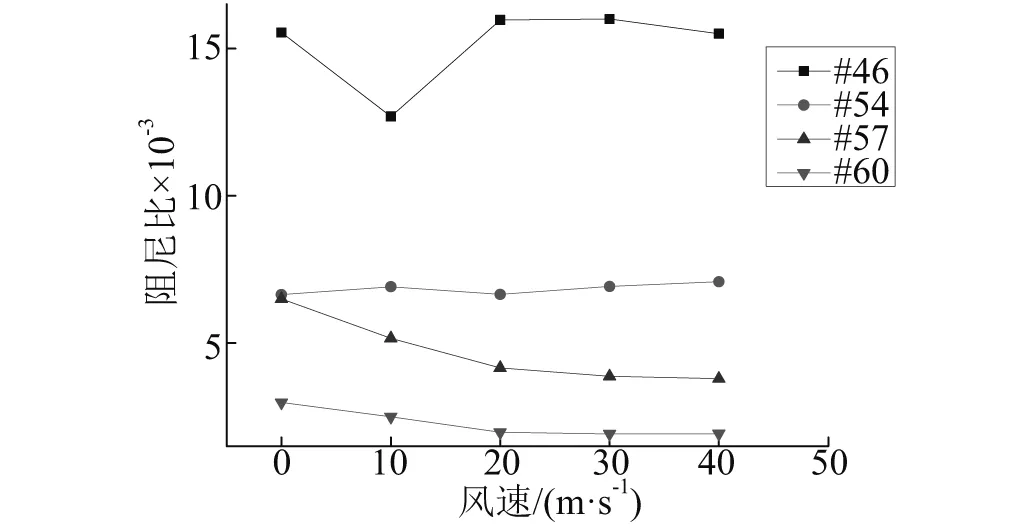
图9 不同吊索在不同风速下的跨中阻尼比Fig.9 The comparison of damping ratio of different length sling

2.5 两端约束情况的影响

为研究吊索两端约束条件对吊索跨中阻尼比的影响，本文选取#46号、#54号、#57号以及#60号吊索分别计算两端为固定端约束和固定铰接约束时，吊索跨中的阻尼比，吊索的基本参数如表7所示，有限元计算得出吊索在不同约束情况下的阻尼比如图10所示，由图10可见，吊索有限元计算时，固定端约束计算出的吊索跨中阻尼比均大于固定铰约束，因此，在进行吊索跨中阻尼比计算时，采用固定铰约束更具有合理性。

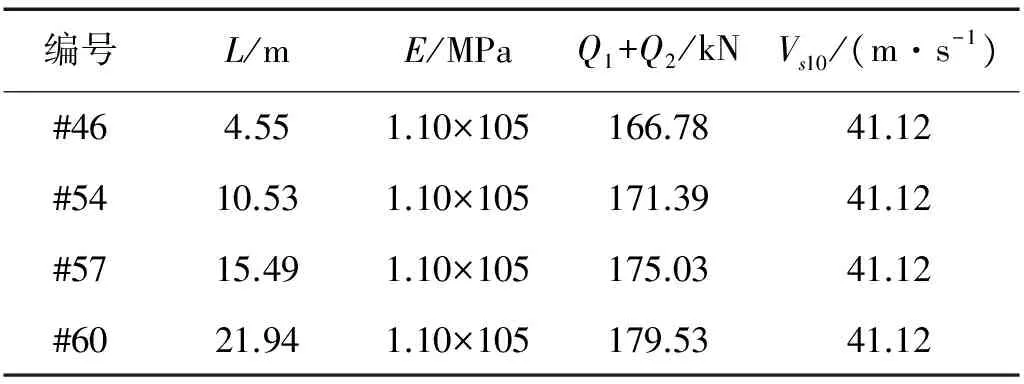
表7 吊索的基本参数

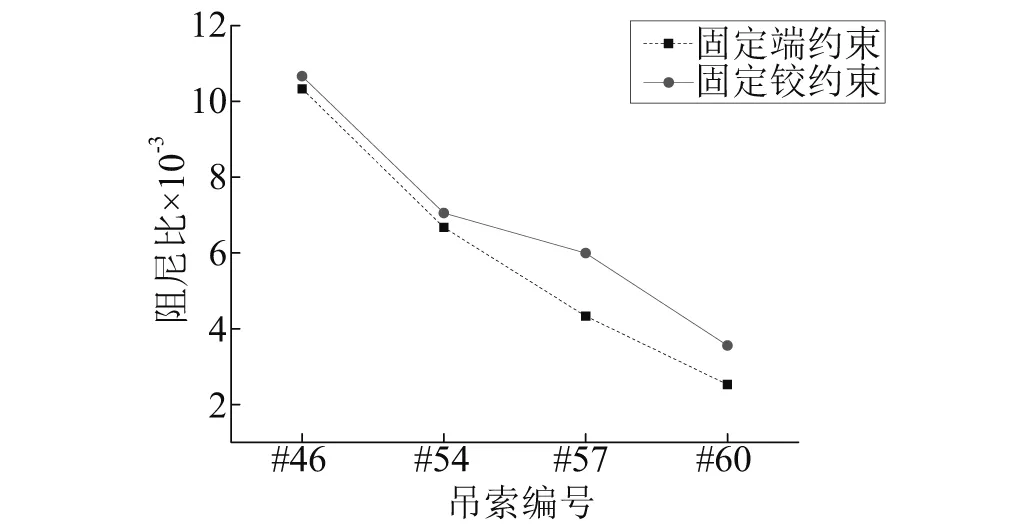
图10 不同吊索在不同约束下的阻尼比Fig.10 The comparison of damping ratio of different constraint sling

2.6 吊索不同位置的影响

为研究吊索不同位置处吊索刚度的变化，本文选取#46号、#54号、#57号以及#60号吊索分别计算吊索在L/8、2L/8、3L/8、4L/8、5L/8、6L/8和7L/8处吊索的刚度值，吊索的基本参数如表8所示，有限元计算得出吊索在不同位置处刚度值如图11所示，由图11可见，吊索的跨中阻尼比一般小于两边阻尼比，从跨中向两端吊索阻尼比逐渐增大；因此在有限元二维流固耦合时，针对同一根吊索，在不同位置选取相同的阻尼比与实际不符。

表8 吊索的基本参数

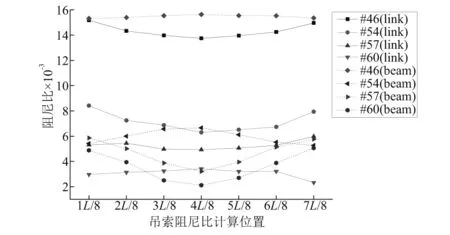
图11 不同吊索在不同位置的阻尼比Fig.11 The comparison of damping ratio of different location sling

3 结 论

(1) link单元建模计算得到的阻尼比大于beam单元，且计算效率更高；beam单元建模计算得到的阻尼比规律性更好，波动性小。

(2) 吊索阻尼比随其初始张力的增大而增大，吊索阻尼比随着长度和直径的增加呈逐步下降的趋势；吊索跨中阻尼比小于两边阻尼比。

(3) 吊索在两端固定端约束时的阻尼比大于两端固定铰约束时的阻尼比；风速大小对吊索阻尼比有较大影响，因此进行吊索流固耦合二维数值模拟计算时，要考虑风速变化对阻尼比的影响，否则会得出错误的结论。

[ 1 ] 于开平，邹经湘，庞世伟. 结构系统模态参数识别方法研究进展[J]. 世界科技研究与发展，2005，27(6)：22-30.YUKaiping，ZOUJingxiang，PANGShiwei.Researchadvanceofmodalparameterindentificationmedthodforstructuralsystem[J].JournalofWorldSci-techR.&D.，2005，27(6)：22-30.

[ 2 ] 张淼，于澜，鞠伟. 基于频响函数矩阵计算阻尼系统动力响应的新方法[J]. 振动与冲击，2014，33(4)：161-166. ZHANG Miao，YU Lan，JU Wei. A new method for computing dynamic response of a damped linear system based on frequency response function matrix [J]. Journal of Vibration and Shock，2014，33(4)：161-166.

[ 3 ] 王慧，刘正士. 一种识别结构模态阻尼比的方法[J]. 农业机械学报，2008，39(6)：201-202. WANG Hui， LIU Zhengshi. A method indentification of structural damping ratios[J]. Journal of Transactions of the Chinese Society for Agricultural Machinery，2008，39(6)：201-202.

[ 4 ] 赵晓丹，徐俊杰，王西富. 利用分段积分识别阻尼比研究[J]. 振动与冲击，2015，34(20)：109-114. ZHAO Xiaodan，XU Junjie，WANG Xifu. Method for damping identification using piecewise integral[J]. Journal of Vibration and Shock，2015，34(20)：109-114.

[ 5 ] 李周，危媛丞.考虑吊索二阶模态的参数振动及其影响因素分析[J]. 华南理工大学学报(自然科学版)，2013，41(2)：94-100. LI Zhou， WEI Yuancheng， Parametric vibration and corresponding impact parameters analysis of suspender cable considering the first two order modals[J]. Journal of South China University of Technologe(Natural Science)， 2013，41(2)：94-100.

[ 6 ] 许福友，丁威，姜峰.大跨度桥梁涡激振动研究进展与展望[J]. 振动与冲击，2010，29(10)：40-49. XU Fuyou， DING Wei， JIANG Feng. Development and prospect of study on vortex-induced vibration of long-span bridges[J]. Journal of Vibration and Shock， 2010， 29(10)：40-49.

[ 7 ] AL-JAMAL H， DALTON C. Vortex induced vibrations using large eddy simulation at a moderate reynolds number[J]. Journal of Fluids and Structures，2004，19(1)：73-92.

[ 8 ] GUILMINEAU E， QUEUTEY P. Numerical simulation in vortex-induced vibrations at low mass-damping[C]//AIAA Computational Fluid Dynamics Conference. Anaheim： AIAA，2001.

[ 9 ] 徐枫，欧进萍. 方柱非定常绕流与涡激振动的数值模拟[J]. 东南大学学报(自然科学版)，2005，35(1)：35-39. XU Feng， OU Jinping. Numerical simulation of unsteady flow around square cylinder and vortex-induced bibration[J]. Journal of Southeast Univerdity(Natural Scievce)， 2005，35(1)：35-39.

[10] 陈文礼，李惠. 基于RANS的圆柱风致涡激振动的CFD数值模拟[J]. 西安建筑科技大学学报(自然科学版)，2006，38(4)：509-513. CHEN Wenli， LI Hui. CFD numerical simulation of vortex-induced vibration of a circular cylinder based on a RANS methed[J]. Journal of Xi’an University of Architecture&Technology(Natural Science)， 2006，38(4)：509-513.

[11] COLLINS J D，YOUNG J P， KIEFLING L A. Methods and applications of system identification in shock and vibration[C]//System Identification of Vibrating Structures. Mathematical Models from Test Data， American Society of Mechanical Engineers. New York： ASME， 1972.

[12] CLOUGH R W， PENZIEN J. Dynamics of structures[M]. New York：Pearson， 1975.

[13] HART G C， LEW M， DIJULIO R M. High-rise building response：damping and period nonlinearities[C]// Proceedings of the 5th World Conference on Earthquake Engineering. Rome：[s.n.]，1973.

[14] 黄宗明， 白绍良，赖明. 结构地震反应时程分析中的阻尼问题评述[J]. 地震工程与工程振动，1996，16(2)：95-105. HUANG Zongming， BAI Shaoliang， LAI Ming. Review on the damping in earthquake response time-history analysis of structures[J]. Earthquake Engineering and Enginering Vibration，1996，16(2)：95-105.

[15] NEWMARK N M， HALL W J. Scismic design criteria for nuclear reactor facilities[C]// Proceedings 4th World Conference on Earthquake Engineering. Santiago：[s.n.]， 1969.

[16] 梁超锋，欧进萍. 结构阻尼与材料阻尼的关系[J]. 地震工程与工程振动，2006，26(1)：49-55. LIANG Chaofeng， OU Jinping. Relationship between structural damping and material damping[J]. Earthquake Engineering and Enginering Vibration，2006，26(1)：49-55.

[17] 陈奎孚，张森文. 半功率点法估计阻尼的一种改进[J]. 振动工程学报，2002，15(2)：151-155. CHEN Kuifu， ZHANG Senwen. Improvement on the damping estimation by half power point method[J]. Journal of Vibration Engineering， 2002，15(2)：151-155.

[18] 周海俊，孙利民，时晨. 摩擦型阻尼器的斜拉索减振实验研究[J]. 同济大学学报(自然科学版)， 2006，34(7)：864-868. ZHOU Haijun， SUN Limin， SHI Chen. A full-scale experimental study on cable vibration mitigation with friction damper[J]. Journal of Tongji University(Natural Science)， 2006，34(7)：864-868.

[19] 巫振弘，薛彦涛，王翠坤，等. 多遇地震作用下消能减震结构附加阻尼比计算方法[J]. 建筑结构学报，2013，34(12)：19-25. WU Zhenhong， XUE Yantao， WANG Cuikun， et al. Research on additional damping ratio calculation methods under frequent earthquake[J]. Journal of Building Structures， 2013，34(12)：19-25.

[20] 李周. 大跨度悬索桥悬吊体系参数振动研究[D]. 广州：华南理工大学，2013.

[21] 公路桥梁抗风设计规范：JTG/T D 60-01—2004 [S].北京：人民交通出版社，2004.

Analysis of factors influencing galloping on the straddle sling damping ratio of long-span suspension bridges

LI Shengli1， ZHANG Shuai1， WANG Dongwei1， OU Jinping2

(1. School of Civil Engineering, Zhengzhou University， Zhengzhou 450001， China；2. School of Civil Engineering ， Harbin Institute of Technology， Harbin 150090， China)

The definition of galloping on straddle sling damping ratio of long-span suspension bridges and its influencing factors analysis are the key problems encountered in the design， and at the moment， the sling damping ratio of practical engineering significance in sling two-dimensional fluid-structure interaction is uncertain. To take advantage of the two-dimensional fluid-structure coupling calculation of wind vibration characteristics of sling in practical engineering， in which， the stiffness and damping ration of the sling section is important. In order to study the damping characteristics of the sling section， free damped vibration and finite element method were used to analyze the influence of the sling damping ratio when sling initial tension， length， diameter， wind speed， constraints and sling position changes. The conclusions are drawn as follows： when the initial tension of sling is increasing， its damping ratio will increase； when the diameter and length of sling are increasing， its damping ratio will decrease. The damping ratio of sling is affected by wind speed. Comparing with the two ends of hinge constraint， the two ends of fixed constraint will be more beneficial to increase the damping ratio of sling. The damping ratio in the middle of sling is the smallest. From the middle to the end， the damping ratio of sling is gradually increasing. Therefore， calculating sling Fludi-Solid Coupling， the value of sling damping ratio differs depending on sling initial tension， length， diameter， wind speed， constraints and sling position.

suspension bridge； sling； free damped vibration； displacement time history； damping ratio； finite element method； fluid-structure interaction

国家自然科学基金资助(51208471)；河南省自然科学基金资助项目(162300410255)；河南省交通运输厅科技项目(2016Y2-2)；郑州大学优秀青年教师发展基金(1421322059)

2016-02-02 修改稿收到日期： 2016-06-28

李胜利 男，博士，副教授，硕士生导师，1979年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.16.013