面元法在串列桨水动力性能预报中的应用＊

侯立勋 王 超 黄 胜

（哈尔滨工程大学船舶工程学院 哈尔滨 150001）

串列螺旋桨是将两特定普通螺旋桨安装在同一轴上以同样转速且相同方向运转的推进器.串列桨在盘面比较大且直径不受限制的情况下，效率和相同盘面比的普通螺旋桨相当，甚至更高一些，对负荷较重或直径受限制的船舶，串列桨效率较高；此外，串列桨能改善普通螺旋桨引起的船尾振动，改善空泡性能，对外界水流变化的适应性较好，结构简单、维修方便，甚至在旧船上也便于改用串列桨.对于串列桨性能预报，多数研究主要局限在实验方面［1－6］.理论方面，毛申睿［7］通过面元法对类似串列桨的叠叶桨水动力性能进行了研究，并同CFD计算结果进行比较，结果偏差较大，此外还没同实验值进行比较分析.

以面元法理论为基础建立了串列桨定常水动力性能计算的数值模型，对3组串列桨进行了水动力性能预报，并通实验值进行了比较分析.

1 串列桨数值计算模型

1.1 基于有升力体面元法原理

根据格林第三定理［8］，考虑串列桨工作于速度为V0的无旋、非粘性、不可压缩来流中，任意一场点P（x，y，z）的扰动势可由以下积分表示

式中：Sb为物面及其尾涡表面；S∞为外边界面，当外控制面距离升力体无穷远时，▽φ→0；RPQ为场点P 物面上其他点Q的距离；∂φ（Q）／∂nQ为物面上Q点速度势的法向导数，满足物面不可穿透条件；E为格林公式参数，其值根据P点与物面S的关系确定，当P在S之内时E为0，P在S上为0.5，P在S 外为1.0.

在边界面的每一部分上，还应满足如下边界条件

式中：V0为远前方来流；Q1为尾涡面上的点；上标＋和－分别表示在尾涡面上、下表面的值.

式中：Δφ为通过尾涡面的速度势跳跃，可记为

利用等压库塔条件求得Δφ的值，该条件要求在升力体尾缘上下表面压力差为零，即

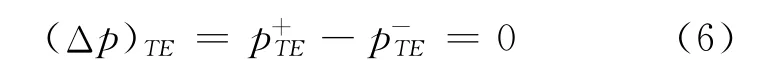
结合等压库塔条件，可求得式（5）的数值解.

1.2 串列桨干扰求解方法

串列桨前后桨之间存在相互干扰，在进行计算时需要考虑诱导速度对彼此的影响［9］.根据积分方程（5），前后桨上的速度势分别为：

式中：Sf，Sfw，Sa，Saw分别为前桨桨表面、前桨桨尾涡表面、后桨表面及后桨尾涡表面；Ωθ为螺旋桨的旋转角速度；Vfa，Vaf分别为后桨对前桨的诱导速度及前桨对后桨的诱导速度；nQ为边界面的单位法向量，指向流场内；Δφ为通过尾涡面的速度势跳跃，其值为桨叶尾缘处的上下表面速度势之差，即Δφ＝φ＋－φ－.

将串列桨的前后桨及他们的尾涡面进行面元划分，其中桨叶径向和弦向均采用余弦分割方式，尾涡面采用线性模型.

式（7）和（8）可离散为

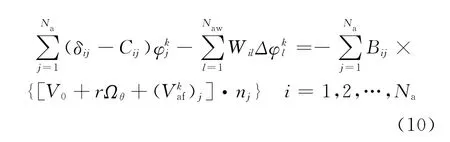
式中：下标f，a分别表示在前桨上和在后桨上；下标af，fa分别表示前桨对后桨的影响和后桨对前桨的影响；Nf，Nfw和 Na，Naw分别为前桨和后桨1个桨叶表面及尾涡面上的面元数分别为第k次迭代时后桨对前桨表面的诱导速度和前桨对后桨表面的诱导速度，其中，＝0＝0分别为前桨敞水状态和敞水前桨在后桨上产生的诱导速度.对式（7）和（8）两边求梯度得

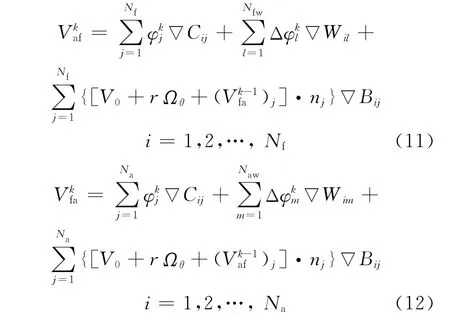
式中：▽C，▽W，▽B为速度影响系数，可由蒙瑞诺发展的解析公式求解.

分别结合前后桨的压力库塔条件，以及通过迭代的方式按式（11）和（12）计算和，可以求解离散方程（9）和（10）.从而求得前后桨上的速度分布，由此可以确定各个面元的切向速度，根据伯努利方程可求得物面上的压力分布，串列桨的性能可表示为：

式中：kt，kq为串列桨的推力系数和转矩系数；T和Q为串列桨的推力和转矩；η为串列桨的效率；J为进速系数；ρ为流体密度；D为串列桨直径；n为串列桨转速.

1.3 计算迭代过程

首先计算前桨的敞水水动力性能，不考虑后桨对前桨的影响［10］，然后将前桨对后桨的诱导速度看作后桨来流的一部分并计算后桨的水动力性能及后桨对前桨的诱导速度，再重新计算前桨（计及后桨的干扰）的水动力性能，如此迭代计算直到kt收敛为止［11］.前后桨干扰迭代流程见图1.

图1 计算流程图

2 算例验证

为验证该性能预报方法的准确性，对3组串列桨进行计算并同实验值进行比较分析，该三组串列桨分别为：CLAU3－30－1，CLB4－40－2和 CLB4－55－2，实验数据均来自文献［1］.在三组算例中，前、后桨直径相同，螺距比之差均不变，无后倾角.

2.1 算例一

应用本文的数值计算方法，对CLAU3－30－1进行计算，该串列桨前后桨叶型均采用AU型，盘面比和毂径比分别为0.30和0.167，叶数为3，前后桨螺距比分别分别取0.8和0.9，前后桨间距取0.20 D，叶错角为30°.图2为 CLAU3－30－1面元划分示意图.

图2 CLAU3－30－1面元划分

用本文预报方法对CLAU3－30－1进行计算所得结果与实验值进行比较见图3，从图中可以看出，计算值与实验值趋势基本一致且吻合良好，在较低进速及较高进速情况下，存在微小偏差，这主要是因为计算程序基于势流理论不考虑粘性的影响，导致低进速时误差偏大；而在高进速时，实际螺旋桨尾涡变形较明显，而计算则是采用无变形的线性尾涡模型，尾涡的影响是导致计算结果产生误差的主要原因.总体而言，误差不超过3.2%.

由于文献［1］仅给出了串列桨总推力、总转矩及总效率的实验值，为对前、后桨推力及转矩进行分析，图4给出了CLAU3－30－1前、后桨推力和转矩计算值随进速系数变化的趋势.从图中可以看出，在进速系数较低时，前桨推力及转矩大于后桨，当进速系数达到0.7时，后桨转矩开始大于前桨，进速系数达到0.8时，后桨推力开始大于前桨，而当进速系数达到0.97时，前桨推力甚至出现负值，串列桨推力主要由后桨提供.

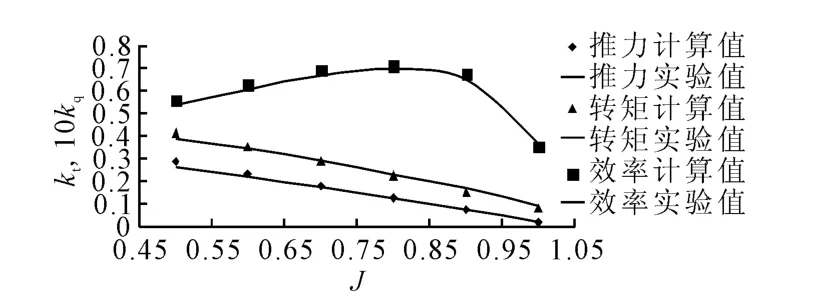
图3 CLAU3－30－1性能计算值与实验值的比较

图4 CLAU3－30－1前、后桨推力和转矩计算值

2.2 算例二

对CLB4－40－2串列桨作为算例二进行计算，前后桨均为B型桨、4叶.前后桨螺距比分别取0.9和1.1，盘面比均为0.40.前后桨间距为0.17D，叶错角为23°，图5为CLB4－40－2面元划分示意图.

图5 CLB4－40－2面元划分

CLB4－40－2的性能计算值与实验值的比较见图6.由图6可见，计算值和实验值趋势一致、吻合良好，但和算例一相比误差偏大，最大达到4%，这主要 是 因 为 与 CLAU3－30－1 相 比，CLB4－40－2前、后桨间距较小，相互之间的扰动更为复杂，尾涡变形难以预测，导致预估误差偏大.

CLB4－40－2的前后桨推力和转矩计算值见图7.由图7可以看出，前、后桨推力及转矩走势与算例一基本一致，但与算例一相比，后桨推力及转矩较早出现大于前桨的趋势，当进速系数为0.42时，后桨转矩就已经开始大于前桨，并且当进速系数为0.68时，后桨推力已开始大于前将，当进速系数为1.1时，前桨推力开始出现负值.这主要是因为与 CLAU3－30－1串列桨相比，CLB4－40－2串列桨具有较大的螺距角，且前、后桨螺距角差值较大，致使后桨推力及转矩相对前桨变化较小.

图6 CLB4－40－2性能计算值与实验值的比较

图7 CLB4－40－2前后桨推力和转矩计算值

2.3 算例三

算例三为CLB4－55－2串列桨，前后桨均为B型桨，4叶.前后桨螺距比分别取1.0和1.2，盘面比均为0.55.前后桨间距为0.21D，叶错角为30.6°，图8为CLB4－55－2面元划分示意图.

图8 CLB4－55－2面元划分

对CLB4－55－2性能计算值与实验值的比较见图9，计算值和实验值趋势一致、吻合良好，与算例一、算例二相比，低进速时，推力偏差较大，最大 达 4.03%，主 要 是 因 为 与 CLB4－40－2 及CLAU3－30－1相比，CLB4－55－2盘面比较大，粘性影响更大，导致低进速条件下误差增大.

图9 CLB4－55－2性能计算值与实验值的比较

就前、后桨推力及转矩而言，变化趋势同算例二大基本一致，但同算例二相比，前将较晚出现负值，主要因为与 CLB4－40－2串列桨相比，CLB4－55－2串列桨具有较大的螺距角，见图10.

图10 CLB4－55－2前后桨推力和转矩计算值

3 结束语

以势流理论为基础，利用面元法提出了一种串列桨定常水动力性能预估方法，通过对三组串列桨进行计算分析后发现，计算值与实验值吻合良好，由于忽略粘性以及采用线性尾涡不考虑变形，致使计算值同实验值产生偏差，但总体而言，误差不大，满足精度要求.

由于流体粘性及螺旋桨尾涡处理是影响螺旋桨水动力性能的重要因素，考虑流体粘性及对螺旋桨尾涡进行非线性处理将做为后续的研究工作，以进一步完善串列桨水动力行预报的方法，从而提高预报精度.

［1］孙 勤，顾藴德，郑淑珍.串列螺旋桨及其设计方法［M］.北京：人民交通出版社，1983.

［2］胡志安.特种推进器［M］.广州：华南理工大学出版社，1996.

［3］王德恂，杨万柏.串列螺旋桨在内河船上的初步应用［J］.武汉水运工程学院学报，1980，3（6）：75－80.

［4］张家龙，徐惠民.导管串列桨敞水性能研究［J］.交通部上海船舶运输科学研究所学报，1985，15（1）：2－10.

［5］陈泽梁，顾其昌，唐瑞平，等.低噪声、低激振半串列螺旋桨的研究［J］.舰船科学技术，1996（2）：18－25.

［6］孙 勤，顾藴德，郑淑珍.串列螺旋桨的模型系列实验和图谱设计方法［J］.中国造船，1979（3）：55－58.

［7］毛申睿.叠叶螺旋桨的水动力性能研究［D］.哈尔滨：哈尔滨工程大学，2010.

［8］SU Y.A study on design of marine propellers by lifting body theory［D］.Yokohama：Yokohama National University，1999.

［9］苏玉民，刘业宝.基于面元法预报导管桨性能的数值计算方法［J］.华中科技大学学报，2012，44（8）：58－59.

［10］ISAY W H.On the interaction between ship and screw propeller［J］.Schiffstechnik，1965（12）：65－76.

［11］郭春雨.螺旋桨－舵附推力鳍相互干扰水动力性能数值计算［D］.哈尔滨：哈尔滨工程大学，2006.