大部件对接中基于单位四元数的iGPS测量位姿比对研究

徐碧菡， 孙涪龙， 赵 罡， 邢宏文

(1.北京航空航天大学中法工程师学院，北京 100191；2.北京航空航天大学机械工程及自动化学院，北京 100191；3.上海飞机制造有限公司，上海 200436)

iGPS (indoor GPS)是一种用于大尺寸空间测量与定位的新型三坐标工业测量系统，其工作原理类似于GPS，利用三角测量原理建立三维坐标系，不同的是采用红外激光代替了卫星(微波)信号。该系统具有测量范围大、精度高、实时性好、系统安装方便等特点[1]，并且支持多用户，即可以使用多个传感器来完成不同的测量任务，如部件定位、指导机器人工作及同步跟踪[2]等，具有广阔的发展前景。目前国内各大航空航天企业已经开始引进iGPS，但对其在飞机装配过程中的应用仍然处于探索阶段。

在大尺寸部件数字化装配的过程中，运用iGPS进行合理布局，可较为便捷地测得部件关键点的位置信息，此时最为关键的问题即为对所测数据进行处理并解算出部件的位姿。但由于iGPS实测数据所采用的坐标系统为测量系统定义的局部三维直角坐标系，与理论模型所采用的设计坐标系进行统一后，实测数据点与理论模型并不一致，因此针对iGPS所测数据与理论模型进行位姿比对研究是进一步利用iGPS辅助部件位姿调整的重要前提。

在测量数据与理论模型进行比对的过程中，需要首先实现刚体姿态解算。目前用于刚体姿态解算的方法主要有：奇异值分解法、三点法、最小二乘法、七参数法、单位四元数法等[3-5]。其中，奇异值分解法虽然求解结果较为准确，然而其应用前提为假设质点经过坐标转换后完全重合，实际在大部件对接中，由于测量误差的存在，质点经过坐标转换后不完全重合，从而影响精度；三点法只适用于不共线的3个点，不适用于iGPS同时测量多个关键点的使用条件；最小二乘法精度受初始值影响大[3]；七参数法在实际使用过程中涉及针对较小旋转角度的线性化[4]，因此若旋转角度较大，就会产生较大的误差，不适宜用于大部件对接过程中的刚体位姿描述；单位四元数法描述刚体的旋转与平移变换直观明了，可针对多点进行计算[5]，并且具有无奇点、不涉及大量三角函数计算等优点，具备作为大部件对接过程中刚体姿态描述方法的条件。

本文根据iGPS本身测量数据的特点，对测量数据的不同形式进行分析与选择，并根据多点同时测量、大旋转角等测量要求，提出一种基于单位四元数的测量数据与理论模型位姿比对计算方法，最后通过实验对该算法进行了分析与验证。

1 大部件对接中的iGPS测量

iGPS由激光发射器、传感器、手持探头、接收器电路和系统软件组成。测量时，发射器产生两个激光平面在工作区域内旋转，转速约为3000 r/min。接收器根据其所能接收到的激光信号，对水平角与垂直角进行测量[6]。

iGPS的测量数据以Frame为单位。Frame与坐标系类似，每个Frame可包含6个自由度信息，即3个方位自由度信息与3个位置自由度信息。但根据测量前用户对Frame中所包含传感器个数及相对位置的不同设定，Frame的自由度信息也会不同。例如，仅包含由单个传感器返回数据的Frame，只包含点位信息，即3个位置自由度信息；包含两个相距固定距离的传感器所返回数据的Frame具有5个自由度信息；而包含4个相对位置固定的传感器(且其中至少3个传感器不共线)所返回数据的Frame，则包含6个自由度信息，即由iGPS底层数据处理软件Surveyor拟合得出的Frame整体的位置与姿态信息。

使用iGPS进行对大部件上多个测量点进行数据测量时，根据Frame的不同数据结构，有两种数据形式可以选择，分别为点位测量与位姿测量。点位测量仅包含3个位置自由度信息。当对多个测量点分别布置单个传感器，并将每个传感器所测数据设定为单独的Frame时，得到的测量数据是每个传感器几何中心的位置坐标。而位姿测量则需将Frame设置为由多个相互位置固定的传感器(且至少3个传感器不共线)及其所测数据构成的整体，得到的数据是由Surveyor经过数据融合计算得出的Frame坐标系原点位置和三坐标轴信息，以及各个点在Frame坐标系下的坐标，但无法获取每个传感器所测的原始数据。

在实际测量过程中，点位测量与位姿测量分别有各自的优点与不足。点位测量形式的优点为可直接采用测量点的原始数据进行计算，并根据实际情况有针对性地设计位姿标定算法；缺点为计算过程可能较为复杂。位姿测量形式的优点为可以直接方便地获取对应Frame的位置与姿态，即测量目标的位置与姿态；缺点为该位姿标定过程由Surveyor自动完成，计算过程涉及多次数据融合，用户难以针对实际测量情况控制位姿标定过程，误差分析较难进行。

因此，本文为避免由系统自身多次数据融合所带来的误差，采用点位测量形式来配置Frame数据结构，即测量各点的位置坐标信息(3自由度)，并以此为基础设计适用于飞机对接过程的模型位姿比对算法，为后续的部件对接提供输入值。

2 基于单位四元数的iGPS测量数据位姿比对算法

将所测点位数据导入理论模型设计软件后，iGPS测量坐标系与理论模型的全局坐标系重合，便可获知在同一坐标系下，两对接部件各自的理论位姿与实际位姿。此时应首先求解部件实测点位信息与理论模型对应点位信息之间的对应关系，即求解两组一一对应点之间的坐标转换关系。根据前文对目前几种常用姿态解算方法的分析，本文采用单位四元数法描述部件姿态。

2.1 基于单位四元数的坐标转换方法

设初始点集为A，目标点集为E，其中目标点与参考点数目相同、一一对应。若每个点集中点数为k，则可记A={ai}，E={ei}，i=1,2,…,k。计算两组一一对应点的坐标转换关系，即为求解满足：

的最佳旋转矩阵R与平移向量T。

根据刚体定点转动理论中的欧拉定理：刚体绕固定点的任一位移，都可由绕过此点的某一轴转过一个角度得到。假设坐标系OXYZ下该旋转矩阵对应刚体在三维空间中绕单位转轴向量v=(ax,ay,az)旋转θ角，则基于单位四元数的坐标转换方法思想[6]如下：

假设旋转转换向量为单位四元数

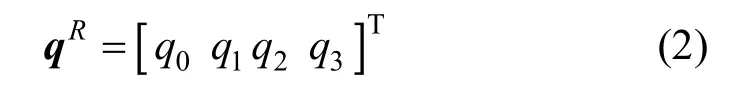
其中各分量分别为[7]：

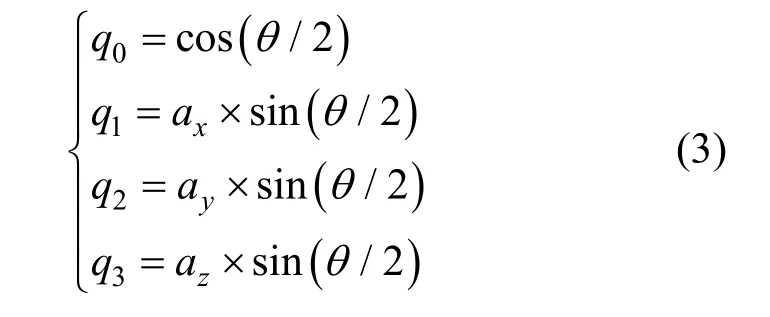
且各分量满足：

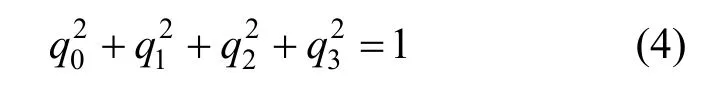
则根据单位四元数可得到3×3的旋转矩阵R(qR)[8-9]：

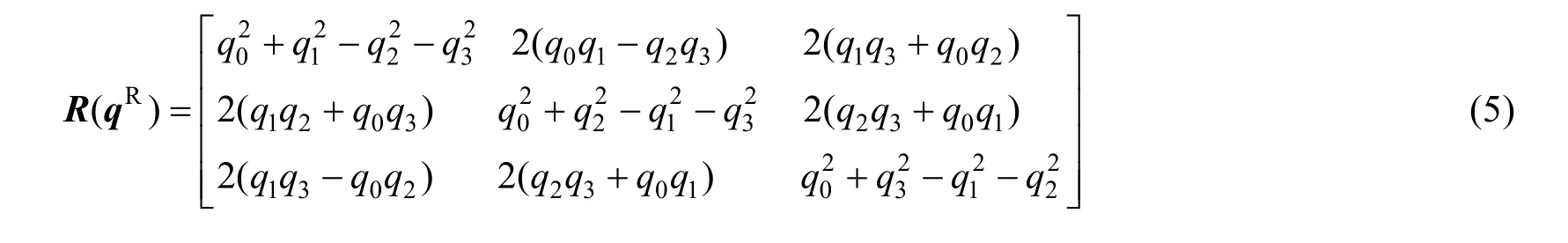
设平移向量为：

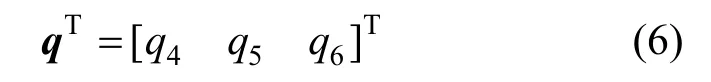
则完整的坐标变换向量即为：

考虑到飞机部件尺寸大刚性差的特点，难以做到坐标转换后与模型完全重合，根据式(1)，结合最小二乘原理设计优化函数如下：

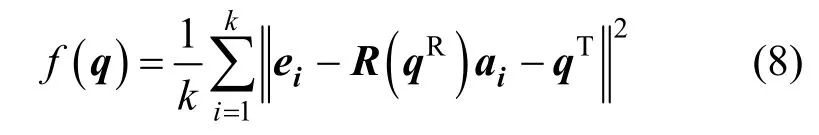
至此求解对应点集间的最佳坐标转换向量问题转化为求使得f(q)具有最小值的坐标转换向量q。

分别求出初始点集A与目标点集E的重心：

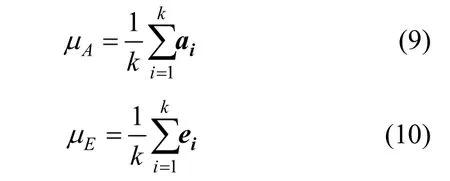
由集合A与集合E构成协方差矩阵：

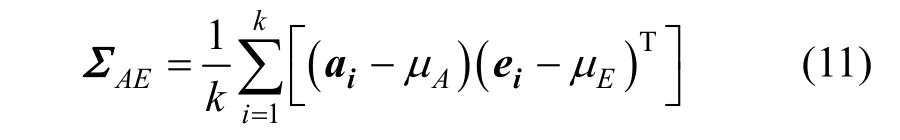
然后利用反对称矩阵：

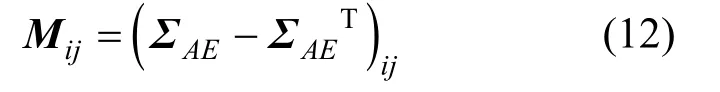
的轮换对称项来构成列向量：

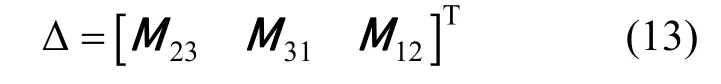
并进一步构造用于求解最优旋转变换向量的矩阵Q(ΣAE)[8]：

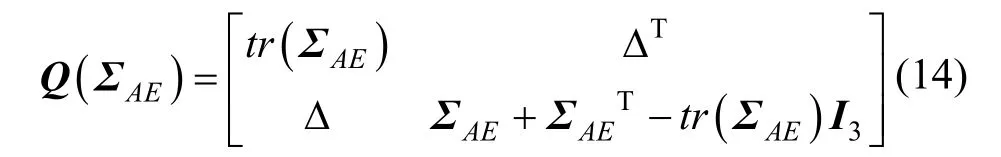
其中，I3为3×3的单位矩阵，tr(ΣAE)为矩阵ΣAE的迹。对应Q(ΣAE)取最大特征值的特征向量qR=[qqqq]T即为最优的旋转变换向量。因此，最优的平移向量为：

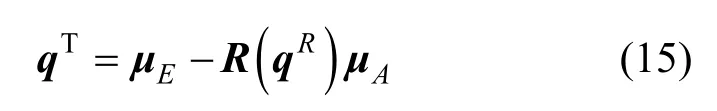
至此，旋转矩阵与平移向量求解完毕，即可实现坐标转换。旋转矩阵所对应的旋转轴v与旋转角度值θ可结合式(3)计算得出。

2.2 iGPS测量数据与理论模型比对方法

假设理论模型中，给定两对接部件M、N，其中M为固定部件，N为移动部件。M与N分别对应于实际部件M′与N′。测量时分别在M′与N′上选定并布置m与n个测量点(m≥3，n≥3)，m与n之间无相互约束关系，可视实际测量需求而定。

首先考虑固定部件，由于其理论模型M在设计坐标系下所有坐标点的信息已知，则可获取设计坐标系下m个测量点的理论坐标信息；实测部件M′上所布置的m个测量点的坐标信息通过iGPS实测获得。此时便有了两组一一对应的坐标值，可采用2.1节中的基于单位四元数的转换方法计算其转换关系Q。此处涉及的转换为将理论模型M上的m个点转换到实测部件位置。

其次考虑移动部件，确定在实际部件N′上的n个测量点后，通过iGPS实测获取相对应的n个坐标点信息。此时由于根据第一步中求出的转换关系Q，即可对移动部件理论模型N上的n个坐标点进行同样的坐标变换，从而求出实际测量场地中移动部件N′的目标位置N′′。

至此确定了移动部件的实际位置N′与目标位置N′′，即可再一次运用2.1节中所介绍的基于单位四元数的坐标转换方法，计算出移动部件到达目标位置所需的坐标转换关系P，从而为后续调姿步骤提供输入数据。

该方法的具体实现流程如图1所示。

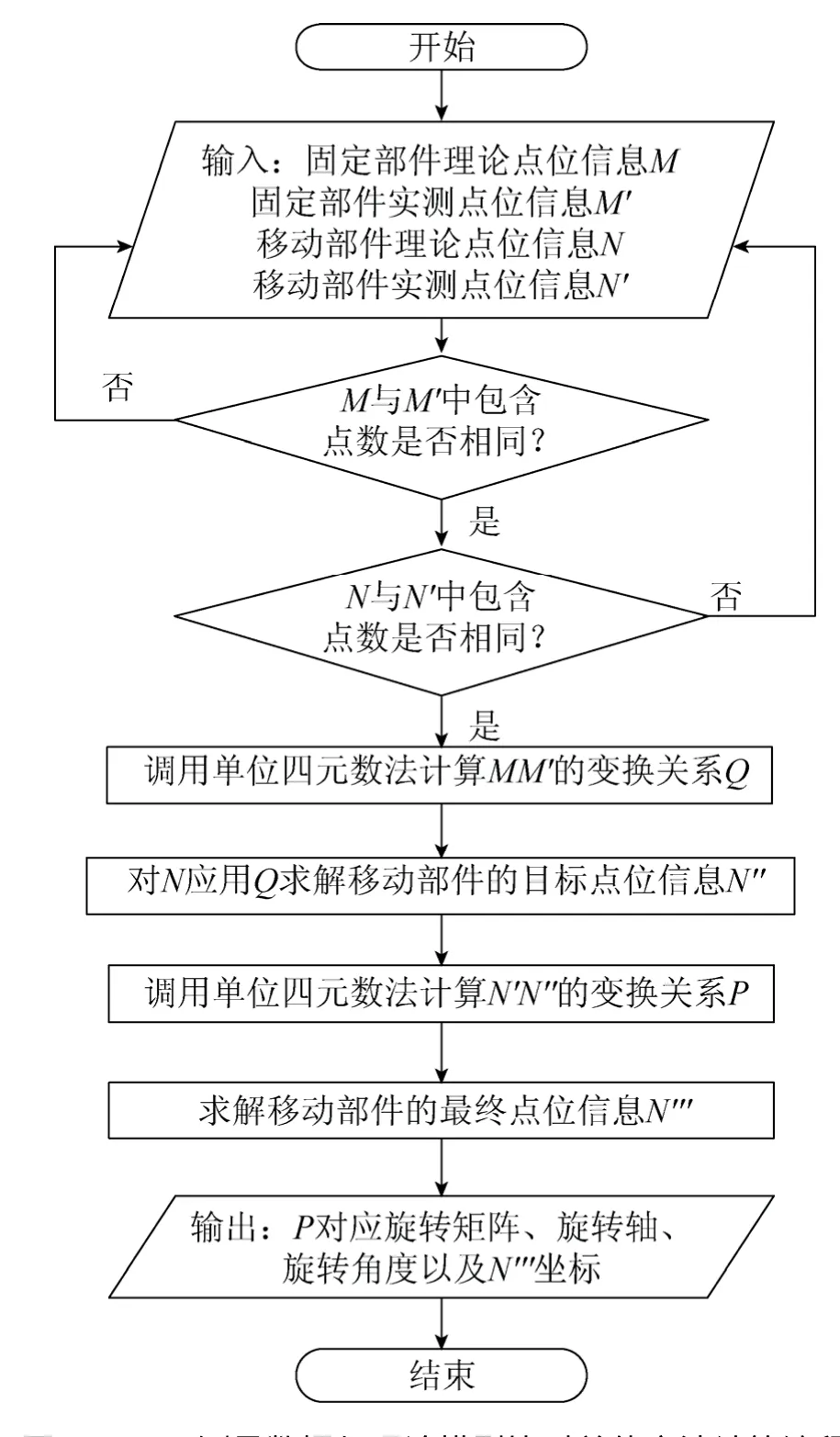
图1 iGPS测量数据与理论模型比对总体方法计算流程

3 实验与分析

3.1 验证实验方案

为验证本文提出的基于单位四元数的iGPS测量数据位姿比对算法的精确度，设计验证实验。整体思路为，首先根据两对接部件实测点位信息与理论点位信息计算相关坐标转换关系；接着在理论模型中两部件对接面上取3个既属于固定部件又属于移动部件的点，用于验证，理想情况即为：计算得到的移动部件目标位姿上的这3个点，与固定部件实测位姿上的这3个点基本重合；于是对这3个点分别应用第一步拟合得出的坐标变换关系，得出固定部件上此3点的实际位置信息，和移动部件上此3点的目标位置信息，计算这两组位置信息之间的误差，考察2节中所提出算法的精度。

具体实验过程如下：

(1) 首先为实际固定部件与移动部件分别选取m个与n个测量点；

(2) 根据2.1节中坐标转换方法，由固定部件实测点位信息M′与其理论点位信息M，计算M向M′的转换关系Q；

(3) 根据式(3)计算Q中单位四元数对应的旋转轴vQ与旋转角度θQ；

(4) 根据2.1节中坐标转换方法，由移动部件实测点位信息N'与其理论点位信息N，计算由N向N′的转换关系S；

(5) 根据式(3)计算S中单位四元数对应的旋转轴vS与旋转角度θS；

(6) 对移动部件理论点位信息N应用转换关系Q，得到移动部件目标点位信息N′′；

(7) 根据2.1节中坐标转换方法，由移动部件实测点位信息N′与移动部件目标点位信息N′′，计算固定部件由N′向N′′的转换关系P；

(8) 根据式(3)计算P中单位四元数对应的旋转轴vP与旋转角度θP；

(9) 对移动部件实测点位信息N′应用转换关系P，得到移动部件最终点位信息N′′′；

(10) 在理论模型中两部件对接面上取3个验证点，则这3个点既属于固定部件，又属于移动部件。理想条件下对接后固定部件和移动部件上的这3个点应当重合。将此3点位置信息记为MNTest；

(11) 对固定部件对接面上的3个点应用变换关系Q，得到固定部件验证点的实际位置信息MTest；

(12) 对移动部件对接面上的3个点应用变换关系S，使其到达移动部件实测位置N′附近，得出移动部件验证点的实际位置信息NTest；

(13) 对NTest的3个点应用变换关系P，得到移动部件验证点的目标位置信息OTest；

(14) 对比MTest与OTest两组验证点的偏差。计算偏差平均值

与标准差σTest。

3.2 实验数据

下面根据3.1节中的实验方案进行3组实验。

为实际固定部件与移动部件分别选取4个测量点，即m=n=4。(实际应用过程中，应根据实际测量点的选取情况确定m与n的取值。)

固定部件理论模型上4个对应点位信息M如表1所示。

移动部件理论模型上4个对应点位信息N如表2所示。

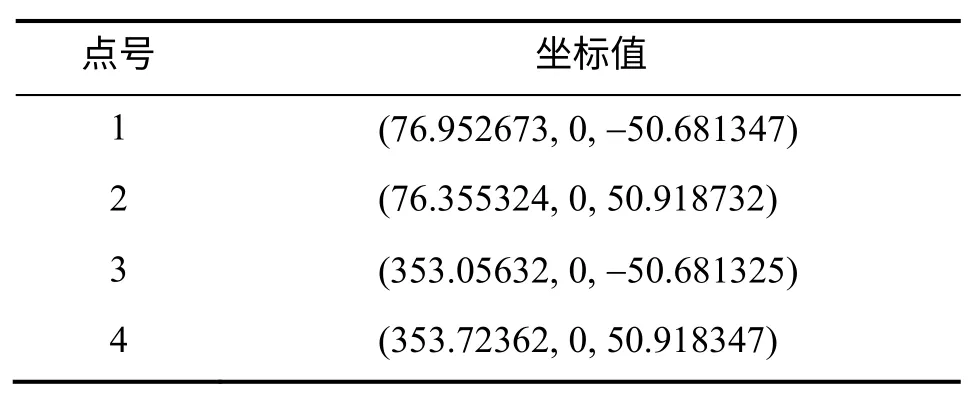
表2 移动部件理论模型对应点位信息N

实验结果如表3所示。计算过程中涉及的各坐标转换关系所对应的旋转轴、旋转角度、旋转矩阵以及平移向量结果也均在表中呈现。

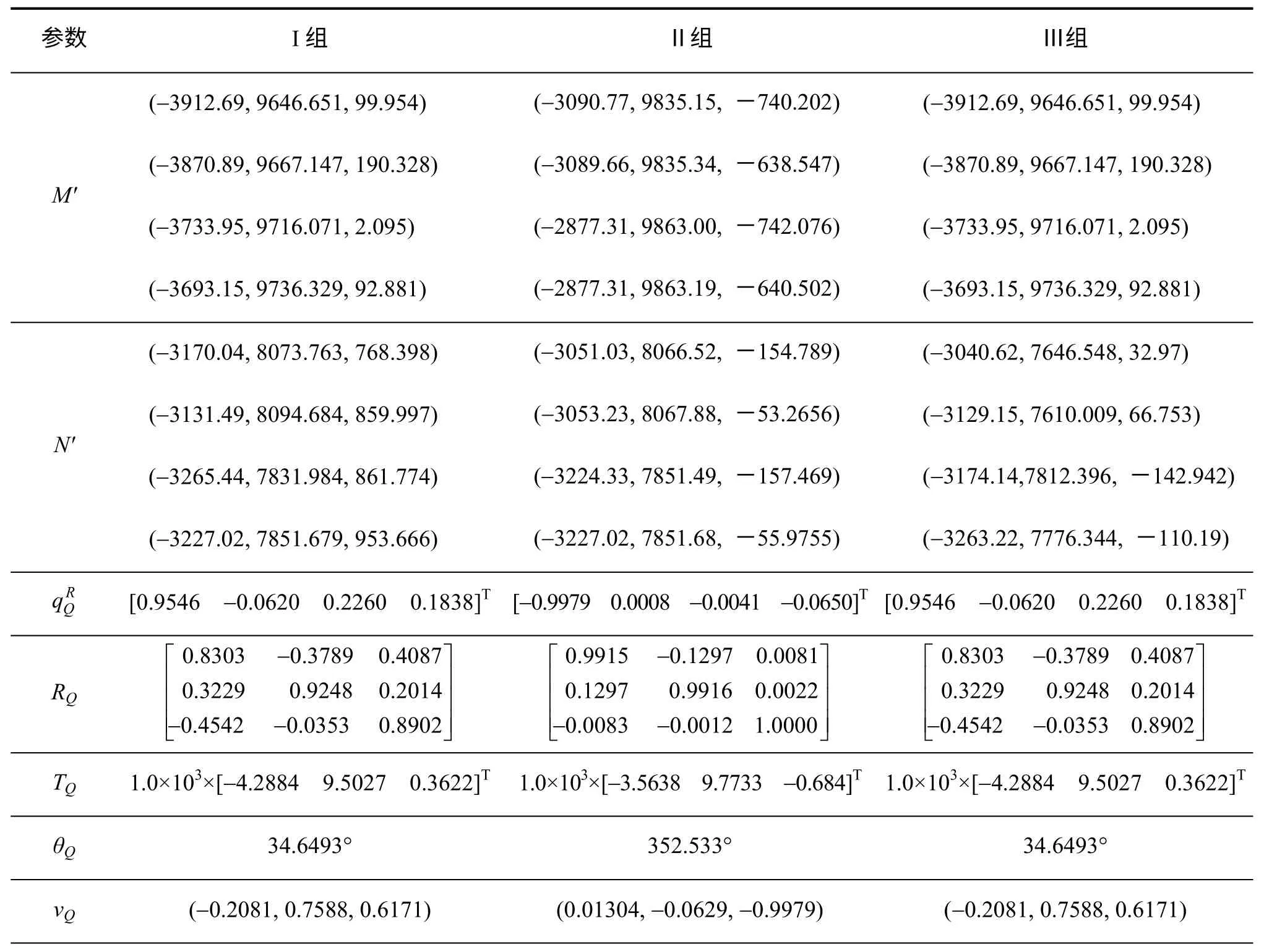
表3 验证实验结果

(待续)

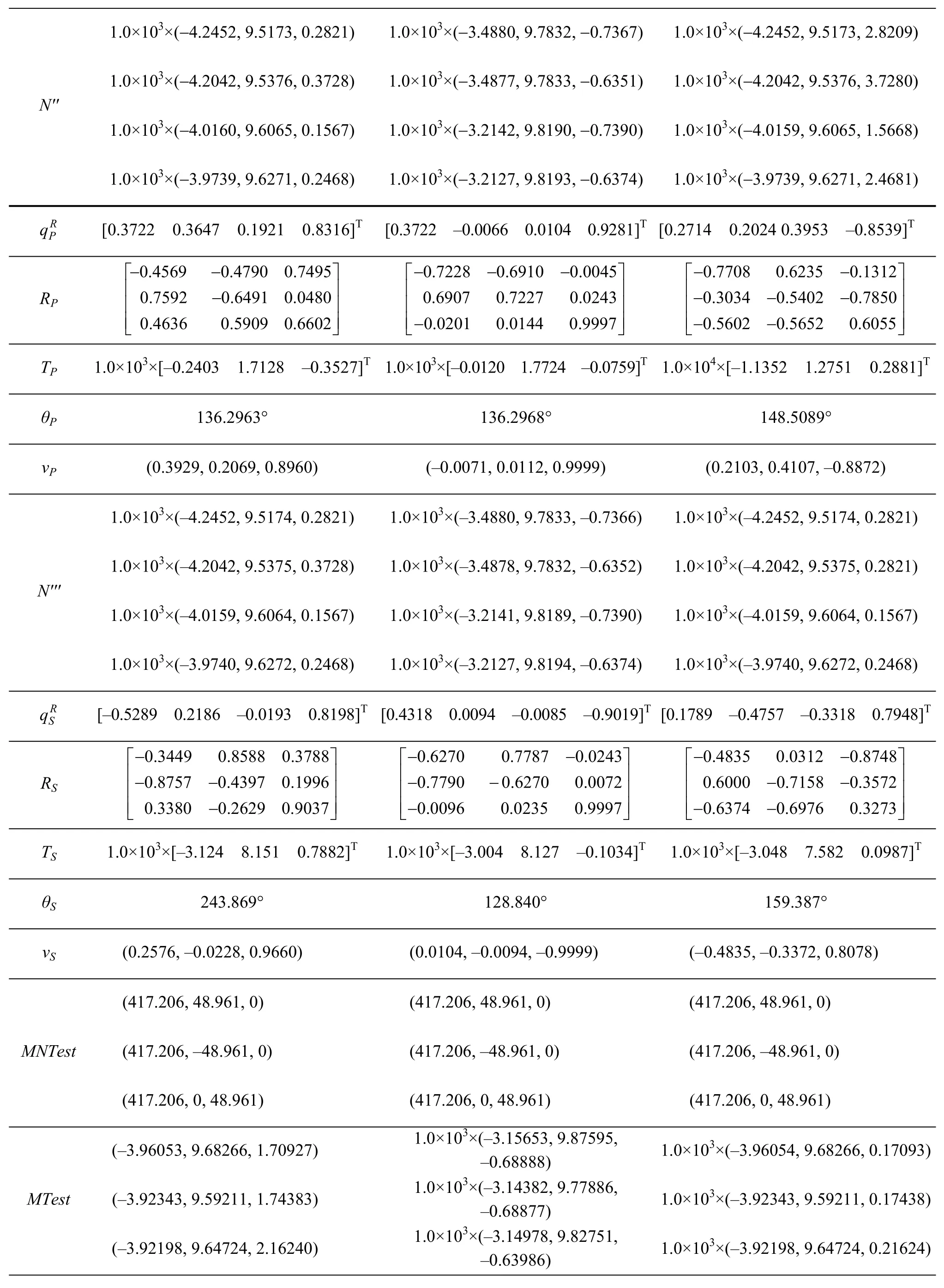
(续表)

(待续)

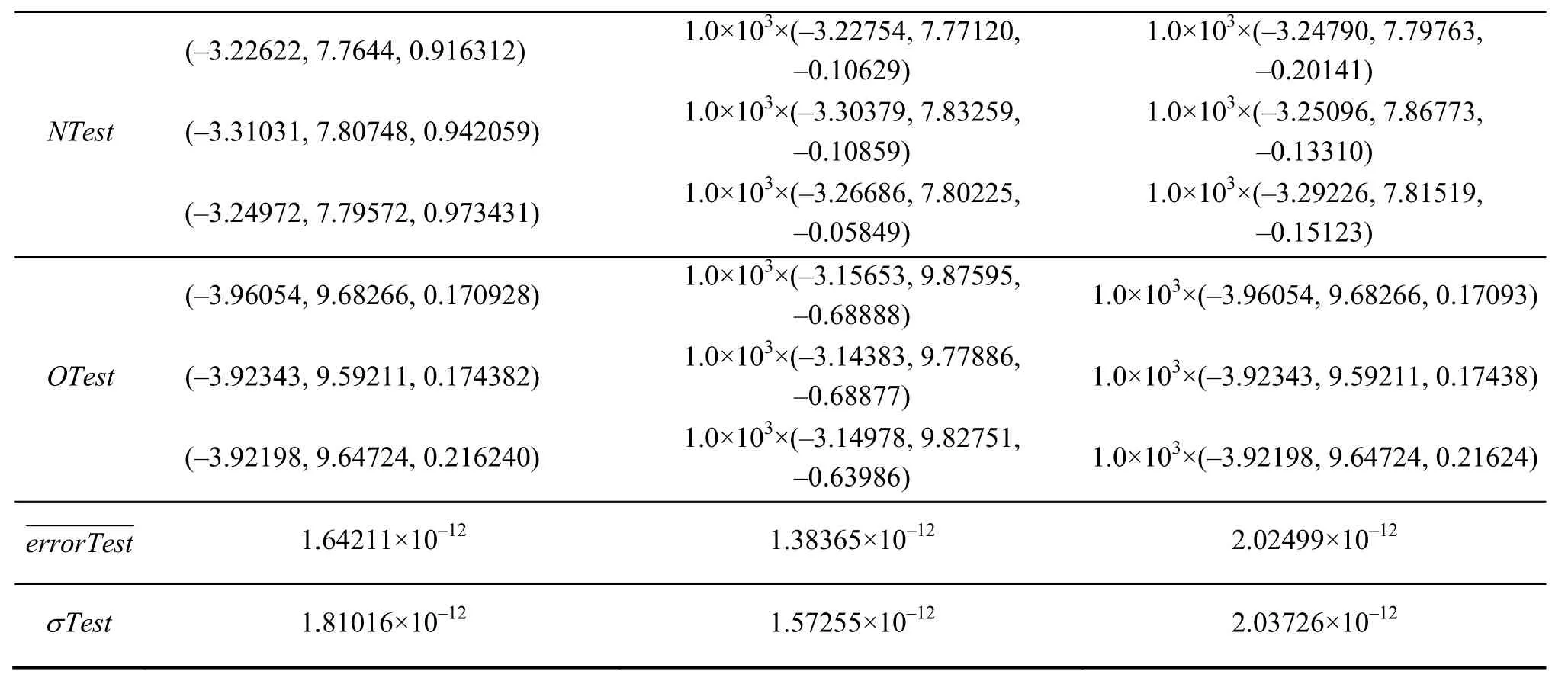
(续表)

3.3 结果分析

由实验结果可以看出，在第I组与第Ⅲ组实验中，固定部件的实际点位信息不变，仅改变移动部件的实际点位信息，因此移动部件由理论模型点位信息向实测点位信息转动角度以及由实测点位信息向目标点位信息转动角度都不同，平移向量也不同，但最终验证点之间的误差都小于10-11数量级。

第Ⅱ组实验与第I组相比，则将固定部件与移动部件的实际位置同时改变，但可以看出，无论是大旋转角还是小旋转角，坐标转换的误差始终小于10-11数量级，标准差也小于10-11数量级。

4 结 论

本文针对大部件对接过程中iGPS多点同时测量、对接旋转角大的特点，提出了基于单位四元数的iGPS测量数据位姿比对算法，用于部件对接过程中测量数据与理论模型的位姿比对。该算法描述位姿变换简洁直观，计算量小，效率高。误差计算与验证实验结果表明，该算法对旋转角大小和平移量无特殊要求，且在不同条件下均有很高的转换精度，能有效适用于iGPS的测量位姿比对计算。

[1]吕景亮,张春富,唐文彦,郝欣宇.Indoor GPS 工业测量系统自标定技术研究[J].计量学报,2011,32(1):12-15.

[2]Norman A R,Schönberg A,Gorlach I A,Schmitt R.Validation of iGPS as an external measurement system for cooperative robot positioning [J].The International Journal of Advanced Manufacturing Technology,2013,64(1-4): 427-446.

[3]罗 芳,邹 方,周万勇.飞机大部件对接中的位姿计算方法[J].航空制造技术,2011,(3): 91-94.

[4]陈 宇,白征东.基于非线性最小二乘算法的空间坐标转换[J].大地测量与地球动力学,2010,30(2):129-132.

[5]Horn B K P.Closed-form solution of absolute orientation using unit quaternions [J].JOSA A,1987,4(4): 629-642.

[6]吴晓峰,张国雄.室内GPS测量系统及其在飞机装配中的应用[J].航空精密制造技术,2006,42(5): 1-5.

[7]Yoon D,Narduzzi M,Shen J.Computing rotation minimizing frames using quaternions [J].Computer-Aided Design and Applications,2012,9(5):679-690.

[8]Besl P J,McKay N D.A Method for registration of 3-D shapes [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2): 239-256.

[9]滕志远,张爱武.单位四元素法在激光点云坐标转换中的应用[J].测绘通报,2010(11): 7-10.