基于B样条曲面插值误差控制的内超环面齿轮齿面建模
2014-03-28姚立纲
洪 玫, 姚立纲
(福州大学机械工程学院,福建 福州 350108)
超环面行星蜗杆传动,如图1所示,由中心蜗杆、行星蜗轮、内超环面齿轮、行星架以及滚动体组成。超环面行星蜗杆传动系统具有优良的传动性能,但这些优良的传动性能必须以较高的传动精度来保证。超环面行星蜗杆传动系统中的关键零件中心蜗杆和内超环面齿轮的齿廓都是复杂的空间曲面,在数控加工中很难保证其精度,导致超环面行星蜗杆减速器在运行过程中存在噪音。国内外学者对超环面行星蜗杆传动的啮合理论[1-2],加工制造[3-4]、承载能力[5]和摩擦、磨损[6-11]等方面进行了深入研究。但是,对于提高这种系统的传动精度,降低其运行过程中存在的噪音研究涉及较少。高精度的三维实体模型是保证数控加工精度的前提条件,因此能否获得精确的中心蜗杆和内超环面齿轮实体模型尤其是精确的齿面模型是解决该问题的关键。
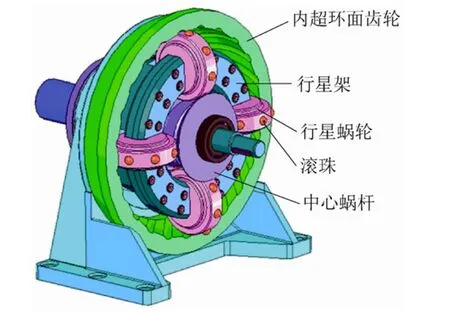
图1 超环面行星蜗杆传动
以往内超环面齿轮和中心蜗杆的实体模型主要采用商用三维建模软件来建立[12]。该方法是利用螺旋齿面特定截面齿廓(法面齿廓)根据一定的路径(螺旋线)扫描生成内超环面齿轮和中心蜗杆齿面的。内超环面齿轮和中心蜗杆齿面的法面齿廓是圆,但是在其他任何平面内,其齿廓却是一条空间曲线,因此,采用该种方法生成的齿面模型存在理论误差。文献[13]利用matlab软件提取内超环面齿轮和中心蜗杆螺旋齿面坐标数据点,并建立了内超环面齿轮和中心蜗杆的离散模型。该方法采用密集采样的方法来提高模型的精度,但是随着坐标数据点数目的增加,计算量也将成倍的增加,而且如何确定坐标数据点的数目以及误差分析计算方法在文中也未有提及。
曲面插值重构作为评定自由曲面零件精度的一项关键技术在各领域中有着广泛的应用,越来越受国内外学者的重视。Zhang和Molenbroek[14]使用B样条曲面重建人体头部的三维模型,运用激光扫描技术能对该模型进行有效地测量,为进一步研究开发计算机辅助人体工程学设计工具奠定了基础。肖思来等[15]应用B样条曲面插值算法建立深孔麻花钻变参数螺旋槽三维精确实体模型。张彦钦和张光辉[16]运用B样条重构蜗轮齿面二次接触区域,由此获得的空间曲面精度高且易于编程实现。Yoo[17]提出基于B样条插值的人类骨骼生物CAD模型的三维重建,该方法创建的骨骼模型适合骨支架设计,有限元分析和医疗诊断。
为提高内超环面齿轮和中心蜗杆螺旋齿面的精度,以内超环面齿轮螺旋齿面建模为例,提出一种基于B样条曲面插值误差控制的内超环面齿轮螺旋齿面建模方法,该方法根据提取的内超环面齿轮螺旋齿面坐标数据点,运用双三次B样条曲面插值重构曲面,通过插值误差分析,根据误差分别特点,对型值点网格不断细分、最终可确定合理的型值采样点数量。
1 B样条曲面插值重构内超环面齿轮螺旋齿面
利用B样条曲面插值内超环面齿轮螺旋齿面的过程如下:首先根据内超环面齿轮螺旋齿面方程提取q向和w向截面线采样点,再根据采样点反求B样条插值曲面的控制点,最后利用所求的控制点构建内超环面齿轮螺旋齿面模型并进行误差计算和分析。
1.1 内超环面齿轮齿面型值点采样
图2所示为剖视的内超环面齿轮三维实体模型。它由螺旋齿面、旋转曲面和两个端面组成。

图2 剖视的内超环面齿轮三维实体模型和单个螺旋齿面
内超环面齿轮螺旋齿面是复杂的空间曲面,其数学模型可由行星蜗轮与内超环面齿轮的啮合关系获得。内超环面齿轮的螺旋齿面是由行星蜗轮齿面的运动包络而成的,行星蜗轮的球形轮齿是内超环面齿轮齿廓的包络母面。

图3 行星蜗轮与内超环面齿轮啮合坐标系
图3表示了行星蜗轮和内超环面齿轮的啮合情况[12]。和分别为内超环面齿轮和行星蜗轮的动坐标系,φ3、φ2分别为螺旋齿面和行星蜗轮齿面相对于它们的静参考坐标系S3、S2的转角。
由齿轮啮合原理[18],根据两共轭齿面的啮合方程和啮合函数可以推导出内超环面齿轮螺旋线方程如下:
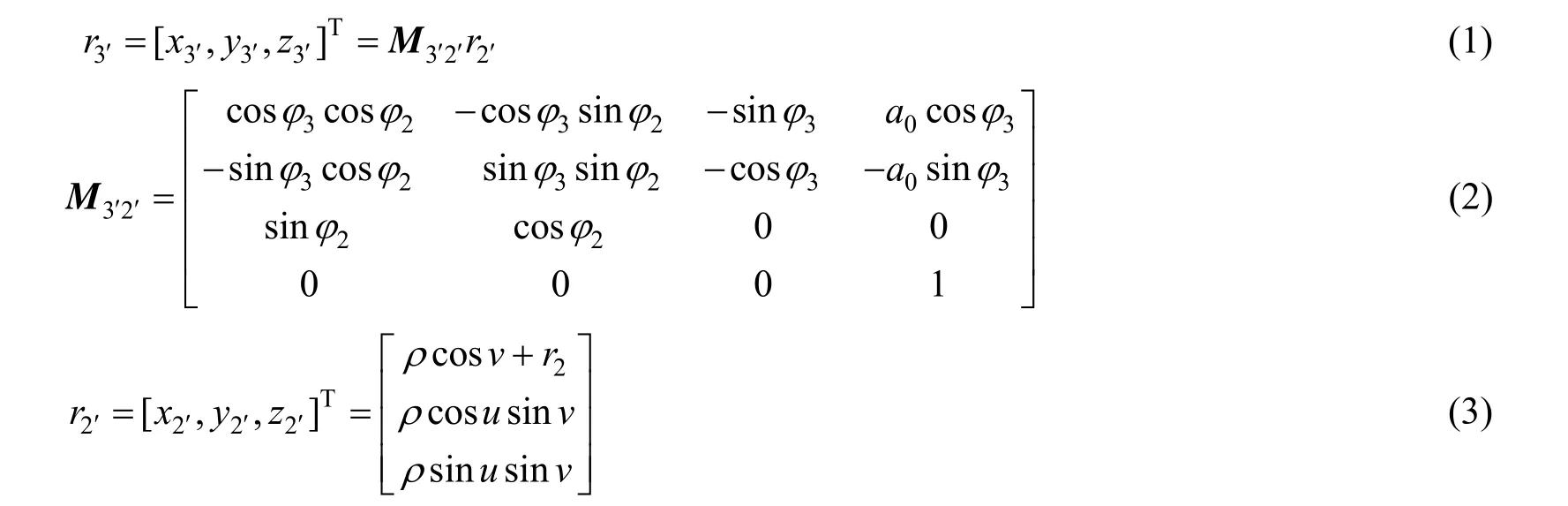
式(1)~(3)中,r2、i23及a0都是已知常数,u、v均为滚珠球面参数,M3′2′是根据行星蜗轮与内超环面齿轮啮合坐标系所得的坐标变换矩阵[12]。当v在取值范围[-π/2,π/2]之间遍历时,螺旋线簇便构成了内超环面齿轮螺旋齿面。采样时,把螺旋线作为w向截面线,把与内超环面齿轮端面平行的截平面(如图4)与螺旋齿面相交所得的截交线作为q向截面线,q向与w向截面线的交点,即为螺旋齿面型值点(如图5)。若m条q向截面线与n条w向截面线求交,可获得m×n个齿面型值点Pi,j(i=1,…,m;j=1,…,n)。这一过程称为螺旋齿面型值点采样。
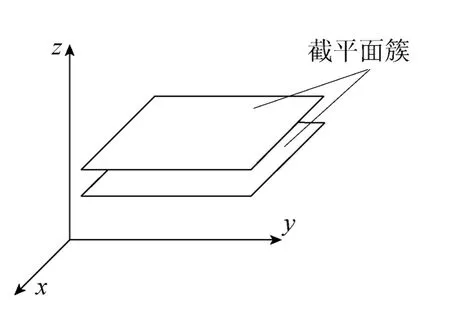
图4 截平面位置

图5 螺旋齿面型值点采样
1.2 内超环面齿轮齿面插值重构
根据上述方法提取的型值点阵分布比较均匀,可考虑采用双三次均匀B样条曲面插值重构内超环面齿轮齿面。为了克服双三次均匀B样条曲面不能插值多边形网格的四个角点的缺点,在两节点矢量的两端取四重节点构造基函数。
1.2.1 双三次均匀B样条曲面的形成
双三次均匀B样条曲面片由包含16个顶点的特征网格Vi,j(i=1,…,4;j=1,…,4)定义,网格Vi,j的任意行或任意列都构成一个特征多边形,由该曲面片的形成过程,可写出双三次均匀B样条曲面片的方程为:

式中:U=[s3s2s1],W=[t3t2t1],Bq,Bw为与控制顶点网格V对应的四重节点B样条基函数[19]。当s和t在[0,1]之间遍历时,就可得到一张双三次均匀B样条曲面片。
1.2.2 反求插值曲面控制点
给定自由端点条件,以提取的内超环面齿轮齿面型值点作依据,反求多边形网格。根据式(3)中v的取值范围[-π/2,π/2],将此区间分成m-1个离散角度的间隔,这样内超环面齿轮螺旋齿面就被离散成m条接触线,如图6所示。

图6 螺旋齿面型值点采样
若用n个截平面与齿面m条接触线求交,可获得m×n个离散数据点,即型值点网格为Pi,j(i=1,…,m;j=1,…,n),其中m和n分别为q向和w向型值点数,则所求的多边形顶点网格应为VI,J(I=1,…,m+2;J=1,…,n+2),其算法如下:
(1) 计算n个q向多边形

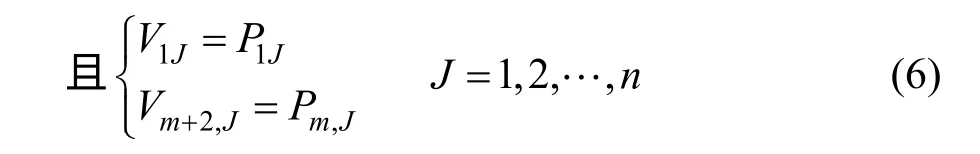
由式(5)~(6)可求得n个q向多边形,其顶点网格为VI,J(I=1,…,m+2;J=1,…,n),令QI,J=VI,J。
(2) 计算m+2个w向多边形

由式(7)~(8)可求得m+2个w向多边形,并具有n+2个顶点,由其构成多边形网格为VI,J(I=1,…,m+2;J=1,…,n+2)。由该网格定义的双三次均匀B样条曲面即可插值给定的m×n个型值点。
1.2.3 插值误差计算
根据上述方法,以6条螺旋线和6个截平面相交为例,根据表1给出的内超环面齿轮螺旋齿面算例参数,在matlab中提取内超环面齿轮螺旋齿面m×n=6×6个齿面信息点作为型值点阵来构造插值曲面。

表1 算例参数
根据式(5)~(8)反求后得到8×8个顶点的控制多边形网格V88(I=1,…,8;J=1,…,8),如图7所示。

图7 控制多边形网格
根据这8×8=64个控制顶点由式(4)可求得5×5=25张曲面片,完成内超环面齿轮螺旋齿面的插值计算。插值计算过程中最关键的是四重节点B样条基函数Bq,Bw的选取。Bq的值取决于曲面沿q向的总曲面片数和该曲面片沿q向的序号[19],Bw的值取决于曲面沿w向的总曲面片数和该曲面片沿w向的序号。此算例中q向和w向的总曲面片数均为5,25张B样条曲面片可表示为Pq,w(q=1,2,3,4,5;w=1,2,3,4,5)。以P2,4这张B样条曲面片为例,根据式(4),方程中的控制顶点网格V和基函数Bq,Bw如下[19]:

为了计算插值曲面与理论齿面之间的误差,取理论齿面网格中间点到相应插值曲面片中间点的距离作为误差来分析。
图8所示为6×6理论齿面网格局部放大图,e1,e2,e3,e4,e5,e6和b1,b2,b3,b4,b5,b6是理论齿面上的型值点,以网格e3b3b4e4为例,只要在两条接触线e3b3和e4b4中间插入一条接触线c1c2,在两条截交线e3e4和b3b4中间插入一条截交线l1l2,c1c2和l1l2的交点即为理论齿面网格的中间点,其坐标为(168.872,-35.2821,36.0)。
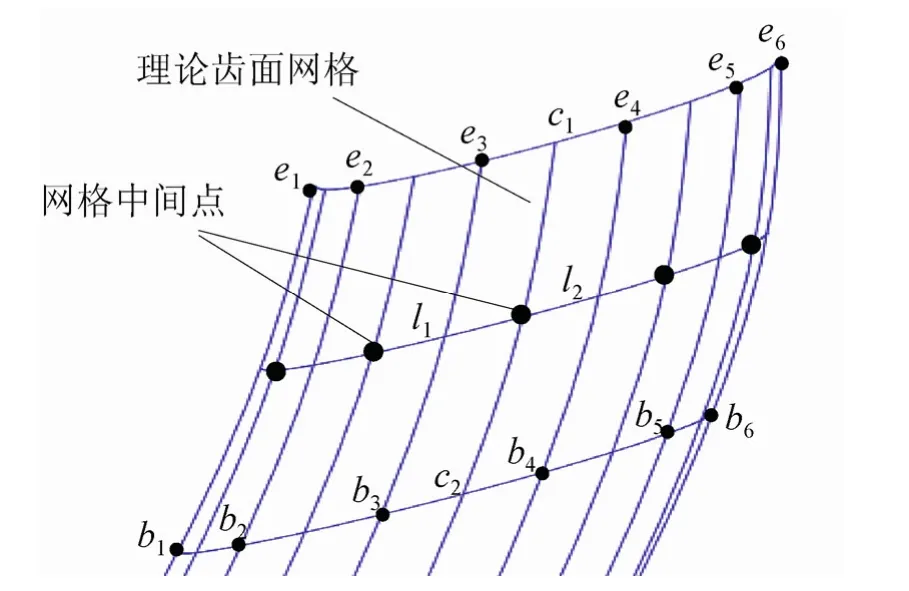
图8 6×6理论齿面网格(局部放大)
图9所示为B样条插值重构6×6型值点曲面片局部放大图,根据式(4),当s和t在[0,1]之间遍历时,即可获得B样条插值曲面片。因此只要当s和t都取0.5时,可获得型值点网格e3b3b4e4对应的插值曲面片中间点的坐标(168.1911,-35.2509,36.0)。
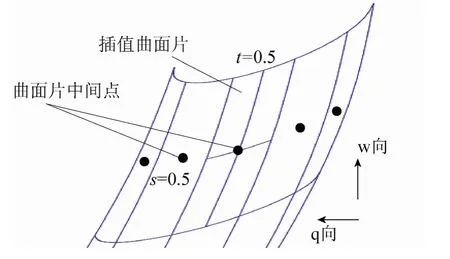
图9 B样条插值曲面片(局部放大)
表2列出了m×n=6×6时25个插值曲面片中间点插值误差计算的结果。

表2 网格中间点插值误差计算结果
根据表2中的数据可看出,最大插值误差存在于螺旋齿面的上下两条边界处,即第1张曲面片和第25张曲面片的插值误差是最大的且数值相等。当螺旋齿面型值点m×n=30×30和m×n=60×60时,采用相同的方法,计算得到最大插值误差分别为0.0444和0.0119,由此可见,网格间距越小,插值误差越小,插值曲面越接近理论齿面。
2 型值点网格细化建模方法
根据上述插值误差分析的结果可知,型值采样点的数目越多,插值曲面的精度也越高,可以采用密集采样的方法来提高螺旋齿面模型的精度,但是型值点的数目该如何确定。针对此问题,以表2中插值误差的计算结果作为依据,提出一种齿面型值点网格细化建模方法。由表2的数据可以看出最大插值误差位于插值曲面的第一张曲面片上,为了减小插值误差,可以将该曲面片对应的型值点网格细化,然后重新构造插值曲面。
型值点网格细化建模方法的流程如图10所示:

图10 型值点网格细化建模方法流程图
具体建模步骤如下:
(1) 选用尽可能少的型值点来插值一张曲面。由于运用双三次均匀B样条曲面进行曲面插值重构至少需要16个型值点,因此采用4条接触线与4条截交线相交所提取的m×n=4×4个数据点作为原始型值点阵,如图11所示。
(2) 运用双三次均匀B样条曲面构建初始插值曲面并计算初始最大插值误差,方法如前所述。
(3) 最大插值误差位于插值曲面的第一张曲面片上,因此可考虑先将第一个型值点网格细化。

图11 4×4齿面型值点网格

图12 第一个型值点网格图和网格细化
图12(a)所示为第一个型值点网格放大图。网格细化的原则是在第一个型值点网格的两条接触线g1h1和g2h2之间插入两条接触线,在两条截交线g1g2和h1h2之间插入两条截交线,由此可以重新获得m×n=4×4个数据点作为新的型值点阵,如图12(b)所示,然后运用双三次均匀B样条曲面构造一张新的插值曲面,计算最大插值误差,最大插值误差仍位于新插值曲面的第一张曲面片中,并将其与给定的误差阈值进行比较。
(4) 比较的结果可能出现两种情况:第一种情况,计算出的最大插值误差小于给定的误差阈值,说明插值曲面的精度已经满足要求,也就是说网格细化的数量足够,只要将其余8个型值点网格细化,细化的网格数量与第一个网格相同即可,细化后的网格数量为34。由此可获得一组1010m×n=×新的型值点阵,用此型值点阵构建的插值曲面满足给定的精度要求。
第二种情况,如果计算出的最大插值误差大于给定的误差阈值,说明插值曲面的精度还未满足要求,也就是说网格细化的数量不够,则重复步骤(3)直到最大插值误差小于给定的误差阈值为止。通过对型值点网格的不断细化,细化的网格数量为32r,r与循环的次数有关,最终可确定一组m×n=(3r+1)×(3r+1)的型值点阵,用该型值点阵插值重构的内超环面齿轮螺旋曲面可满足给定的精度要求。表3中给出了不同型值点数量最大插值误差的计算结果。

表3 不同型值点数量最大插值误差的计算结果
根据上述齿面型值点网格细化方法可确定合理的型值点数目,当m×n=82×82时,用双三次均匀B样条曲面对此型值点阵进行插值重构,最大的插值误差为0.0055 mm。将该型值点阵导入三维建模软件中,即可获得内超环面齿轮螺旋齿面模型。为了验证此方法的可行性,建立了单个螺旋齿面模型(如图13所示),并进行了数控加工(如图14所示)。对加工后的实体进行了表面粗糙度的测量,测量结果如图15所示,表面粗糙度Ra的数值为0.005897 mm,此结果与最大插值误差的数值近似,可以说明此建模方法是可行的。

图13 单个螺旋齿面模型

图14 数控加工实体

图15 表面粗糙度测量数据
3 结 论
内超环面齿轮形状的特殊性和齿廓的复杂性给数控加工带来了困难,加工精度很难保证。本文提出根据内超环面齿轮齿面螺旋线方程,运用截平面法提取型值点阵,采用双三次均匀B样条插值方法,计算理论齿面网格中间点到相应插值曲面片中间点的距离,将此距离作为插值误差进行分析。通过误差分析,确定最大插值误差所在位置。通过最大插值误差与给定误差阈值的比较,确定网格细化的次数,最终获得一组型值点阵,插值重构得到满足精度要求的内超环面齿轮螺旋齿面模型。运用此方法在获得高精度的内超环面齿轮齿面模型的同时合理地确定了型值点的数目。运用B样条插值重构曲面,可通过不断修正多边形网格顶点来调整曲面形状,最终获得一张满意的齿廓曲面,这也为内超环面齿轮齿廓的修形提供了思路和手段。
[1]Yao Ligang, Dai Jian S, Wei Guowu, Li Huamin.Geometric modelling and meshing characteristics of the toroidal drive [J].Transaction of ASME, Journal of Mechanical Design, 2005, 127(5): 988-996.
[2]Yao Ligang, Dai Jian S, Wei Guowu, Cai Yingjie.Comparative analysis of meshing characteristics with respect to different meshing rollers of the toroidal drive [J].Mechanism and Machine Theory, 2006, 7(41):1237-1255.
[3]Yao Ligang, Dai Jian S, Li Huamin.Mathematical modelling and manufacturing of the internal toroidal tooth profile [J].Journal of Mechanical Engineering Science, 2004, 218(9): 1043-1051.
[4]Yao Ligang, Dai Jian S, Wei Guowu.Error analysis and compensation for meshing contact of toroidal drive [J].Transaction of ASME, Journal of Mechanical Design,2006, 128(3): 526-533.
[5]Peeken H, Troeder C, Tooten K H.Borechnung und messung der lastverteilung im toroidgetriebe [J].Konstruction, 1984, 36(3): 81-86.
[6]许立忠, 黄 真.超环面行星蜗杆传动摩擦理论研究[J].中国工程科学, 2002, 4(3): 63-67, 77.
[7]许立忠, 杨育林, 黄 真.超环面行星蜗杆传动弹流润滑状态研究[J].机械工程学报, 2002, 38(9): 114-117.
[8]许立忠, 张志慧, 闻 岩.滚锥包络环面蜗杆传动磨损研究[J].润滑与密封, 2001, (6): 16-17, 19.
[9]许立忠, 杨盛福, 景常海.滚锥包络环面蜗杆传动润滑研究[J].润滑与密封, 2001, (5):31-32.
[10]Xu Lizhong, Huang Zhen, Yang Yulin.Contact stress for toroidal drive [J].Trans of ASME, Journal of Mechanical Design, 2003, 125(3): 165-168.
[11]Xu Lizhong, Huang Zhen, Yang Yulin.Mesh theory for toroidal drive [J].Transaction of ASME, Journal of Mechanical Design, 2004, 126(2): 551-557.
[12]魏国武.超环面行星蜗杆传动的关键技术研究[D].福州: 福州大学, 2004.
[13]郭贵勇.超环面行星蜗杆传动建模与弹性啮合分析[D].福州: 福州大学, 2009.
[14]Zhang B, Molenbroek J F M.Representation of a human head with bi-cubic B-spline technique based on the laser scanning technique in 3D surface anthropometry [J].Journal of Applied Ergonomics, 2004, 35(5): 459-465.
[15]肖思来, 周志雄, 左小陈, 孙振梅, 汤爱民, 蓝仁浩.深孔麻花钻变参数螺旋槽的数字建模研究[J].中国机械工程, 2011, 22(21): 2555-2559.
[16]张彦钦, 张光辉.平面包络环面蜗杆副精确实体模型的建立[J].重庆大学学报, 2010, 33(7): 12-17.
[17]Yoo Dongjin.Three-dimensional surface reconstruction of human bone using a B-spline based interpolation approach [J].Journal of Computer-Aided Design, 2011,43(8): 934-947.
[18]吴鸿业.齿轮啮合理论[M].哈尔滨: 哈尔滨工业大学出版社, 1979: 1-60.
[19]朱心雄.自由曲线曲面造型技术[M].北京: 科学出版社, 2000: 1-156.
