三角网格特征边识别的一种有效方法

张 炜， 金 涛

(1.浙江机电职业技术学院机械工程学院，浙江 杭州 310053；2.浙江大学化工机械研究所，浙江 杭州 310027)

三角网格在求解科学与工程计算的问题中向来扮演着重要的角色，而近年来，有关网格特征边识别的课题正在成为一个研究热点。这是因为，随着三维扫描仪的成本下降和质量提升，三角网格的生成变得轻车熟路，点云或网格曲面在计算机辅助设计(computer aided design，CAD)与计算机图形(computer graphics，CG)中使用更加普遍，作用日益凸显，从而大大促进了网格重建[1]、网格编辑[2]、网格参数化[3]、网格光顺[4]等一系列以网格计算和网格变换为主题的研究。而上述研究都是以网格特征边识别为先决条件的。另一方面，借助扫描仪与CAD软件(如AutoCAD、Pro/E，、Unigraphics、Solidworks等)，人们能够快速获得逼近三维几何物体表面的三角网格，这些三角网格的数据主要保存在一种业已成为行业标准的STL文件当中；而基于STL文件的计算机辅助制造(computer aided manufacturing，CAM)，必须以三角网格的特征边识别为首要前提。综上可知，给出一种鲁棒的网格特征边识别算法，对CAD/CAM/CG而言，实为当务之急。

关于网格特征边已经有大量识别算法。文献[5]首先通过判断曲率的局部极值来识别网格的特征点，然后根据主曲率分析方法(principal curvature analysis，PCA)用3次B-样条把这些特征点连接成特征线。文献[6]提出了利用网格边的二面法向夹角(2个网格三角形平面的法向夹角)和边角(两条相邻的边的外转角)之间关系的一种算法来识别特征边。此后文献[7]又改进了这种算法，并进一步提出了一种识别C2不连续网格边的算法。文献[8]以张量投票(tensor voting)为工具对网格顶点进行分类，然后用区域扩张合并的递归算法对网格进行分块。假设其中n是顶点p的1-ring的三角形ii的法向，分别是矩阵A的特征值和相应的特征向量。所谓张量投票是指用分别逼近曲面法向(e1)和主曲率(e2,e3)。但是文献[9]指出，这种逼近方式有以下缺点：①法向对权重十分敏感而且符号未定，可能是内法向也可能是外法向；②当顶点所在的边的二面法向夹角大于90°时，用逼近法向的效果比用为优；③当顶点所在的边的二面法向夹角等于90°时，三个特征向量都不能很好地逼近法向。文献[10]通过网格重建得到一个各向同性的对特征敏感的度量，然后利用局部邻域的积分不变量来识别多尺度网格上的特征。以上算法在精度上都不尽如人意。文献[11]通过统计网格边的二面法向夹角信息，计算出二面法向夹角的平均值和标准差来确定特征边的阈值，并通过递归的算法来识别特征边。但该文有一个明显的缺点：不能识别二面法向夹角比较小的特征边，如图1所示。最近，文献[12]利用网格顶点处的法向和曲率半径等离散微分几何工具给出了一个判别特征点的指标，并给出了识别网格特征点的鲁棒算法。但该算法存在以下问题：①文中给出的指标十分不合理，影响了识别的准确度；②文中只是给出了特征点的识别算法，并没有给出特征边的识别算法，难以在CAM中加以使用。

综上所述，迄今为止，各种网格特征边识别算法都存在着明显缺陷，严重地阻碍了以网格计算和网格变换为主题的研究，也影响了基于STL文件的CAM的正常开展。因此，本文深入剖析了文献[11]和文献[12]的理论机理中的软肋，首先改造文献[12]所提出的识别特征点的指标，进而利用改造所得的新指标来改进文献[11]中的算法，得到了一种识别网格特征边的新的鲁棒的算法，并予编程实现。在此基础上，本文把新算法与文献[11]中的算法作了深入的数值实例比较，并给出了图形显示与绘制。这些例子表明，文献[11]的算法易导致失效，而本文的算法可挽救这种失效。尽管文献[11]是2004年发表的会议论文，但是本文与之比较还是有意义的，原因如下：①近年来，在网格特征边识别并没有取得突破性的发展，没有一个鲁棒的算法可以在机械制造领域得到广泛的应用；②文献[11]在特征边识别领域有着重要的意义，近年来许多相关的文献都与之做出比较，如文献[6,12]。

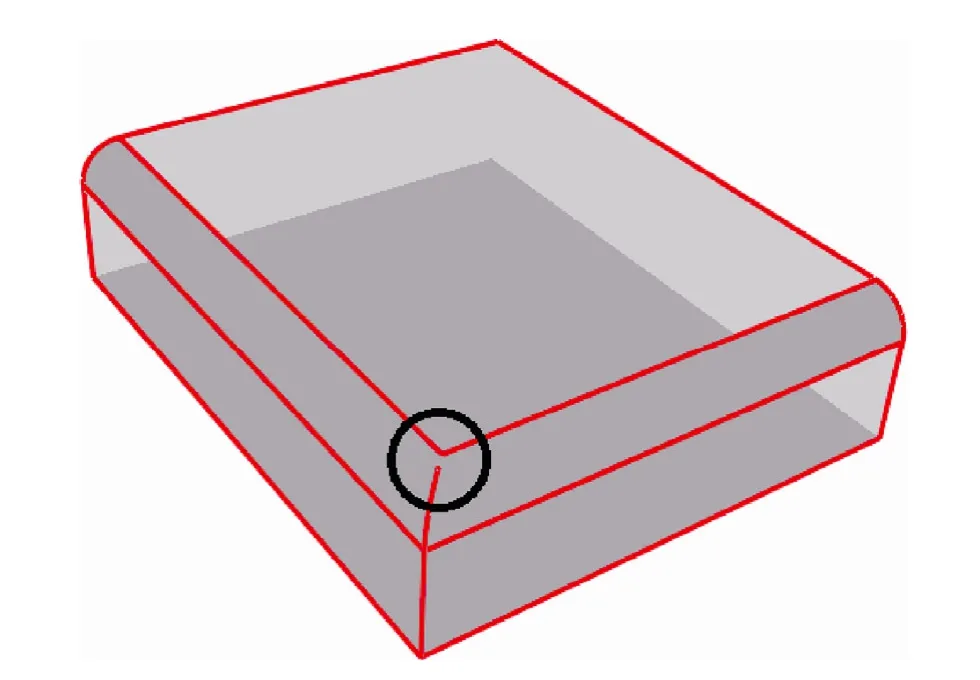
图1 用文献[11]中的算法所得到的网格特征边

1 准备知识

1.1 网格顶点的法向

由于网格曲率的估计依赖于网格顶点法向，这里先给出网格法向的计算方法。必须指出，网格顶点的法向是不能精确计算的，已经有很多关于网格顶点的法向估计的文章。其中最常用的两种方法是加权平均和张量投票。正如文献[9]所指出的，张量投票方法存在着一些缺点，所以本文采用加权平均来估计网格顶点的法向。假设顶点p的1-ring三角形的法向为vi,i=1,...,m，m是顶点p的1-ring的三角形数量，则顶点p处的法向可计算如下：这里wi是权重，本文取wi为三角形的面积。

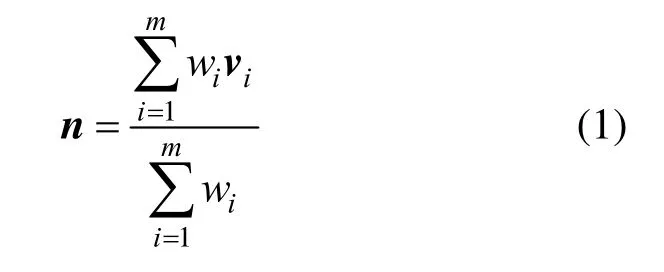
1.2 网格顶点的曲率

由于网格顶点的曲率也是不能精确计算的，已经有很多关于网格顶点的曲率估计的文章。 常用的网格顶点曲率估计的方法有离散算法[13]、曲面局部拟合法[14-15]、曲率张量投票法[8]等。文献[15]指出，用离散算法估计网格顶点的曲率在某些情况下是不准确的，而曲率张量投票的逼近算法也存在着很多缺点[9]，因此本文采用曲面局部拟合的方法来估计网格顶点的曲率。文献[14]采用二次曲面去拟合顶点与其1-ring的顶点，这种拟合方法是一定插值该顶点的。文献[15]也采用二次Bézier曲面去拟合顶点与其1-ring的顶点，不过这种拟合方法是不一定插值该顶点的。尽管文献[14]中的曲率估计方法不是最准确的，但是用它来估计网格的局部微分性质已经足够了。为了论文的完整性，下面简单介绍一下这种方法。

在网格顶点p处建立一个局部坐标系，其中坐标系的z轴为该点处的外法向。采用二次曲面s(u,v)=(u,v,au2+buv+cv2)来拟合该顶点及其1-ring的顶点，这里u,v都是局部坐标系下的自变量。假设该顶点的1-ring顶点在局部坐标系下的坐标值为(ui,vi,hi),i=1,...,m，可以得到下面的线性方程组：

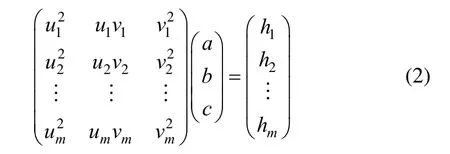
用最小二乘法求解式(2)可得二次曲面的系数a,b,c。由此可得该顶点处的主曲率和相应的主曲率方向如下：

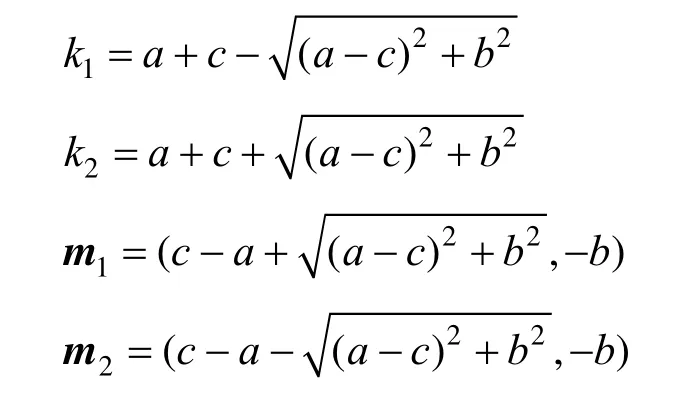
假设向量m在主曲率方向m1,m2张成的平面上，且m与m1的夹角为θ，则曲面s(u,v)沿m方向的法曲率为：

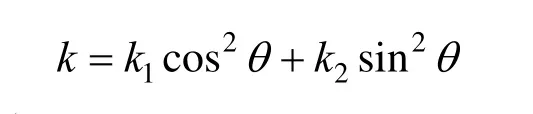
1.3 特征点判别指标

文献[12]给出了一个判断沿网格顶点某个方向的光滑程度的指标：

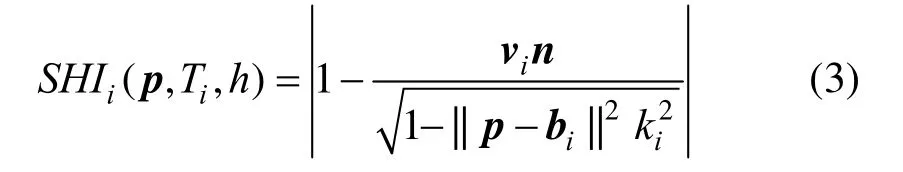
这里iT是顶点p邻域的三角形，bi是该三角形的重心，vi是该三角形的法向，ki是在向量pbi和法向n张成的平面上顶点p处的法曲率(见图2)。由于文献[12]中并没证明式(3)中的变量满足：

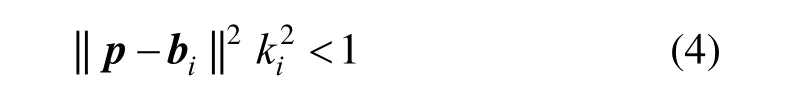
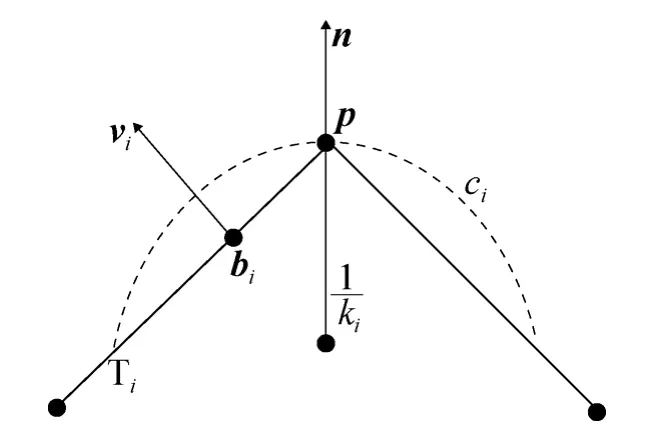
图2 顶点沿某个方向的光滑程度

而且在实验中发现式(4)在某些情况下是不成立的，这将干扰识别的准确性。在网格大小比较均匀处，式(4)是成立的，因为从图2中可以看出，若在该处拟合出来的曲面是比较接近三角形，则在bi处的曲率半径会小于，即式(4)成立。但是，在网格大小不均匀处，拟合的二次曲面曲率比较大，则在bi处的曲率半径会大于。进一步地，可以发现当这种情况出现时，点p处是不光滑的。因此，本文把式(3)改成如下：

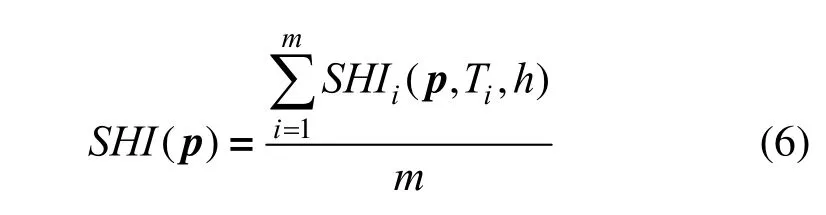
若SHI(p)大于某个给定的阈值α，则认为顶点p为特征点，否则认为顶点p为光滑点。

2 特征边识别的新算法

2.1 基本几何体分析

我们对Unigraphics导出STL文件的基本几何体(见图3)进行分析，可得出如下结果：误差取默认的输出误差，圆柱体的上下底面的边界为特征边，侧面的边(非底面的边)的最大二面法向夹角为9°；圆锥体的底面边界为特征边，侧面的边(非底面的边)的最大二面法向夹角为8°；球体本身没有特征边，球表面网格边的最大二面法向夹角为4.5°；圆环体本身没有特征边，圆环表面网格边的最大二面法向夹角为6.6°。这里网格边的二面法向夹角定义为以该边为公共边的两个三角形的外法向夹角。

2.2 阈值的确定

本文的算法需要用到2个阈值α1,α2，其中α1是网格边的二面法向夹角的阈值，而α2是网格特征点的阈值。根据2.1节的分析，可将把二面法向夹角大于20°的网格边定义为特征边，而把二面法向夹角介于[α1,20°]之间的网格边成为次特征边。若式(6)中定义的指标SHI(p)大于α2，则认为顶点p为特征点。这里的阈值α1,α2都可以通过用户交互确定。另外，若α1取得比较大，则可能会漏掉一些特征边，若α1取得比较小，则可能会识别出一个错误的特征边。α1的取值还跟模型的网格大小质量等有关，所以无法确定出一种最优通用的阈值方案。一种常用的方案是取所有二面法向夹角的均值作为阈值的初始值。对于阈值α2, 可以参考文献[12]给出的一种通过求解某个最优化问题的方法来确定该阈值。

图3 基本几何体的特征边分析

2.3 识别算法描述

文献[12]中的识别特征点指标比文献[11]中的根据最小主曲率的主曲率方向来识别特征点的准确度要高，故用改造文献[12]的识别特征点的指标来改进文献[11]的算法，能提高识别的准确度。本节给出网格特征边识别的新算法描述。假设输入的网格模型是M=(V,E,F)，这里V,E,F分别是模型的顶点、边、三角形的数组。

网格特征边识别算法：

输入.三角网格模型M=(V,E,F)，以及用户的输入参数μ,λ。

输出.三角网格模型的特征边数组L。

步骤1.初始化一个临时数组tempL，计算网格模型的相关数据，如网格边的二面法向夹角， 网格特征点的判断指标SHI(p)。

步骤2.计算网格边的二面法向夹角的平均值θavr和标准差θsd，计算阈值α1=θavr+μθsd，α2=λ。

步骤3.对网格模型作一次平面检测。

步骤4.对每个网格顶点p进行检测，判断该顶点是否为特征点。若指标SHI(p)大于α2，则认为顶点p为特征点，否则认为它为光滑点。

步骤5.对每条网格边进行检测。 若该边的二面法向夹角大于20°，则把它放入特征边数组L；若该边的二面法向夹角属于[α1,20°]，则把它放入临时数组tempL。

步骤6.对临时数组tempL中的边进行过滤。若边的两个端点中不都是特征点，则把该边从tempL删除。

步骤7.对临时数组tempL中的边按二面法向夹角从大到小的顺序进行排序。这里采用二分法排序，时间复杂度为O(nlogn)。

步骤8.对临时数组tempL中的边进行特征边判别。假设p1,p2为该边的两个端点，若与p1,p2相连的边中已经有两条或两条以上的特征边，则认为该边不是特征边，否则认为该边是特征边并将之放入特征边数组L。

3 数值例子

本文实现了文献[11]中的算法，并将之与本文的新算法作比较。实现新算法的PC配置如下：Intel Core2 CPU T7250，RAM 2 GB。本文算法是用C++和OpenGL实现的。图4给出的是一个经过圆角处理的长方体，从图1可以看出，文献[11]的算法不能得到二面法向夹角很小(黑色圈出的部分)的那些特征边，而图4中用新算法却得到了所有的特征边。图5和图6分别给出了一个叶轮模具和一个零件模具的网格模型，图5(b)和图6(b)中用黑色圆圈圈出的部分皆为没有识别到的地方，由之可以看出，文献[11]的算法易导致失效，而本文的算法挽救了这种失效。

图4 本文算法所得到的网格特征边

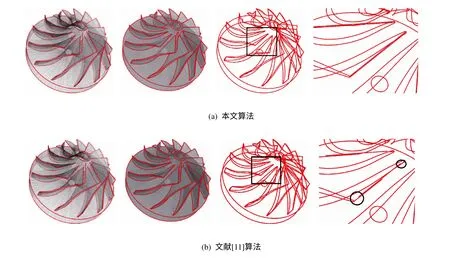
图5 对叶轮的网格特征边作识别对比 (最右边的一列图是右2列图中黑色矩形内部分的放大图)

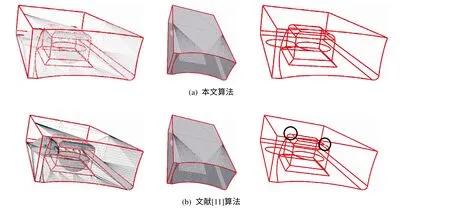
图6 对零件的网格特征边作识别对比

4 总 结

本文改进了判别网格特征点的指标，进而给出了一种识别三角网格特征边的新算法。该算法能够很好地识别出用文献[11]中的算法不能识别的二面法向夹角比较小的网格边，从而在时间复杂度一样的基础上大大提高CAM中模具加工的效能。本文以后的工作是将本文的算法推广到C2不连续网格边的识别。

[1]Volpin O, Sheffer A, Bercovier M, Joskowicz L.Mesh simplification with smooth surface reconstruction [J].Computer Aided Design, 1998, 30(11): 875-882.

[2]Zhang Shaoting, Huang Junzhou, Metaxas D N.Robust mesh editing using Laplacian coordinates [J].Graphics Models, 2011, 73(1): 10-19.

[3]Morigi S.Feature-sensitive parameterization of polygonal meshes [J].Applied Mathematics and Computation, 2009, 215(4): 1561-1572.

[4]Li Zhong, Ma Lizhuang, Jin Xiaogang, Zheng Zuoyong.A new feature-preserving mesh-smoothing algorithm [J].The Visual Computer, 2009, 25(2): 139-148.

[5]宁上官, 刘 斌.三角网格模型特征线提取方法[J].华侨大学学报(自然科学版), 2010, 31(5): 487-490.

[6]Jiao Xiangming, Heath M T.Feature detection for surface meshes [C]//Proceedings of 8thInternational Conference on Numerical Grid Generation in Computational Field Simulations.Honolulu, 2002:705-714.

[7]Jiao Xiangming, Bayyana N R.Identification of C1and C2discontinuities for surface meshes in CAD [J].Computer Aided Design, 2008, 40(2): 160-175.

[8]Kim H S, Choi H K, Lee K H.Feature detection of triangular meshes based on tensor voting theory [J].Computer Aided Design, 2009, 41(1): 47-58.

[9]Jiao Xiaoming, Alexander P J.Parallel feature-preserving mesh smoothing [C]//Proceedings of International Conference on Computational Science and Its Applications.Singapore, 2005: 1180-1189.

[10]Lai Yukun, Zhou Qianyi, Hu Shimin, Wallner J,Pottmann H.Robust feature classification and editing [J].IEEE Transaction on Visualization and Computer Graphics, 2007, 13(1): 34-45.

[11]Baker T J.Identification and preservation of surface features [C]//Proceedings of 13thInternational Meshing Roundtable.Williamsburg, 2004: 299-310.

[12]Di Angelo L, Di Stefano P.C1continuities detection in triangular meshes [J].Computer Aided Design, 2010,42(9): 828-839.

[13]Myers M, Desbrun M, Schroder P, Barr A H.Discrete differential geometry operators for triangulated 2-manifolds [M].Berlin: Springer-Verlag Press, 2002:34-57.

[14]Haman B.Curvature approximation for triangulated surfaces [M].Berlin: Springer-Verlag Press, 1993:139-153.

[15]Razdan A, Baea M.Curvature estimation scheme for triangle meshes using biquadratic Bézier patches [J].Computer Aided Design, 2005, 37(14): 1481-1491.