基于细分粒子的刚体破裂动画

陈沸镔，谢步瀛，冉修远

(同济大学建筑工程系，上海 200092)

日常生活中，脆性破裂是一种很常见的现象，如瓷器的破碎，混凝土砖墙的倒塌。如何对这种现象进行模拟是计算机图形学领域的一个重要研究方向，在计算机游戏、影视特效、虚拟现实等领域中有着广泛的应用。

在计算力学和材料力学领域，对于固体脆性破裂数值模拟的研究已经进行了数十年，研究人员提出了大量的数值计算方法。目前大致有两种数值离散方法：基于网格的方法和无网格方法。有限元法是(finite element method，FEM)一种典型的基于网格的方法，它是通过将连续体模型剖分成一个个网格单元，根据各个网格单元的特性来计算网格节点上的属性。有限元法的主要缺陷是对网格剖分的要求较高，当由外力产生的网格形变太大的时候，对控制方程求解的精度会产生很大的影响。相对而言，近年来引起研究人员极大兴趣的无网格(粒子)方法由于在计算时不受到背景网格的约束可以有效地解决上述基于网格方法的缺陷。然而，在图形学领域，使用基于物理的方法对脆性破裂进行动画生成的研究却为数不多。基于物理的固体脆性破裂动画主要是以断裂力学以及材料力学为基础，采用数值离散方法，来分析固体在外力作用下产生的内部应力。

与数值分析方法不同的是，在计算机图形学中，为了达到相对快速的模拟速度，适当的模型简化以及对数值方法的进行优化是非常重要的。与此同时，如何增强模拟的细节也是引起研究人员广泛关注的另一个问题。单方面的追求计算速度往往导致模拟的结果过于粗糙，然而使用分辨率较好的原始模型又会带来计算代价较大的问题。如何能在提高模拟框架的计算速度的前提下又能够给出相对较好的模拟精度是一个具有挑战性的问题。针对这种问题所提出的局部细分技术能够很好的地解决这一矛盾，局部细分技术的主要思想是以一个相对较大的尺度进行初始离散建模，然后通过在需要增强细节的部分进行局部的细分方式来重采样生成较小尺度的局部模型以此来提高模拟的细节。

本文提出一种基于细分粒子的刚体脆性破裂的模拟框架。首先将四面体化的固体网格模型绑定到一系列粒子上。然后使用光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)方法来求解固体碰撞时产生的内部应力。通过更新SPH粒子所绑定网格节点的状态，能够快速的对开裂断面进行维护从而减少在网格重构和拓扑更新上的计算代价。最后提出一种细分粒子的算法，从而在提高系统的计算效率的同时又增强了模拟效果的细节。

1 相关工作

与脆性破裂动画研究有关的工作主要可以从数值计算模型和几何模型两个方面来进行阐述。

从数值计算模型的角度来说，在图形学领域最早进行固体破裂动画的研究可以追溯到上世纪80年代末。Terzopoulos等[1-2]最早使用基于物理的方法来进行弹塑性变形和破裂模拟，他们使用的数值模型是有限差分方法。同一时期研究较多的模型还有质点-弹簧模型[3]或者质点-约束模型[4]。上述模型的主要缺点是不能精确的计算开裂点的位置和方向，以此模拟的结果并不十分逼真。在破裂模拟中，更为精确的数值模型是基于连续介质力学[5]。作为一种典型的基于网格的数值离散方法，有限元法首次被O'Brien等[6-7]用来求解线弹性力学方程进行脆性和塑形破裂的模拟，从而得到了较为真实的效果。在此基础上，许多研究人员针对有限元方法进行了各种改进，如对物理模型的简化[8]，提高模拟的速度[9]以及加强计算的精度[10]。基于网格的数值方法的缺点在于得到计算精度高的结果需要高质量的网格，而无网格方法不存在这种问题。Pauly等[11]使用移动最小二乘法(moving least square，MLS)来求解应变张量从而进行脆性和塑性破裂的模拟。其不足之处在于为了保证计算的正确，每个粒子对其邻接粒子的位置和数量有较高的要求。Liu等[12]采用了无网格局部 Petrov-Galerkin方法(meshless local petrov-Galerkin，MLPG)解决了这个问题，但是在求解的时候需要计算一个大规模的线性方程组，因此计算的开销较大。

从几何模型的角度来说，破裂模拟实际上是对一个整体的网格进行拓扑的切割操作，因此，如何选择一个合适的固体表面网格模型对模拟速度以及仿真结果有着重要的影响。固体的曲面模型大致可以分成2种：显式的网格模型与隐式的网格模型。显式模型在模拟过程中不需要在每个时间步长内反复进行表面网格的生成，只需要处理节点间的关系，因此处理代价低、计算速度高，但由于网格是初始计算时就生成好的，因此进行几何切割操作较为复杂。如Müller等[9,13]使用的四面体网格模型和规则八面体网格模型、Molino等[14]提出的虚节点算法等，均是对初始的网格做了一定的约束条件之后才进行切割操作的。隐式曲面模型是使用隐式曲面方程来生成固体的表面，对复杂曲面变化的适用性较好而且不存在切割操作的问题，但是由于需要在每个时间步长内进行网格的计算，因此计算代价较高。如文献[11]中提出的一种基于点的隐式跟踪曲面模型，其开裂面的生成是通过构造型立体几何表达法(constructive solid geometry，CSG)进行生成的。

综上所述，本文脆性破裂模拟的框架提出了一种基于粒子和网格的混合模型。在数值离散方面使用了基于粒子SPH方法进行求解。在几何方面使用了一种将网格绑定于粒子上几何模型，能够快速对开裂固体曲面进行维护操作。

2 基于粒子的固体模型

2.1 固体的离散

本文的数值计算模型是基于粒子的，因此首先需要将初始模型离散成一系列粒子。同时考虑到开裂断面的生成，一个合适的固体几何模型对于开裂时几何拓扑的修改和模拟结果的渲染也是极其重要的。基于这两点的考虑，本文使用了一种将离散四面体绑定到粒子上的显式曲面几何模型。

在数值计算中，网格生成是一个关键性的技术，如何将一个连续的计算区域离散成一系列的四面体是一个重要的研究课题，作为数值计算和计算几何的交叉研究内容，四面体网格生成技术经过近20年的发展已逐渐成熟并衍生出大量的网格生成技术，在这之中，Delaunay三角剖分由于其网格高质量特征和对复杂区域良好的逼近性受到研究人员的广泛关注，是目前最流行的全自动网格生成方法之一。因此，本文选用Delaunay三角剖分来进行初始的四面体网格生成，详细的生成算法可以参见文献[15]。

首先，将整个固体区域通过Delaunay三角化剖分成一系列的四面体，在每个四面体的形心位置分配一个粒子。粒子的半径r可根据四面体的体积V进行计算：为了进行后续的拓扑维护操作为每个粒子保存2种信息：原四面体的顶点坐标和指向相邻粒子的指针(图1中的“链接”)。四面体顶点坐标(图1中蓝色的点)主要有2个作用：维护开裂的曲面的生成以及计算内部应力。当粒子的邻接粒子数小于4时将该粒子定义为固体表面粒子，其作用是进行碰撞处理和计算虚位移状态。在初始化时，所有表面粒子所对应的三角形面都将加入到一个三角形网格中作为固体的曲面模型。 SPH粒子所保存的信息可以快速的进行开裂面的维护，将在第4节中具体介绍。

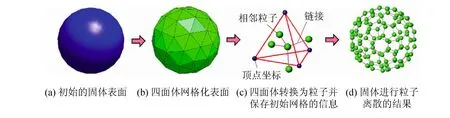
图1 固体离散建模过程

2.2 线弹性固体力学模型

本文破裂模拟框架的力学模型是基于线弹性固体力学。在线弹性固体力学中，固体的应力与应变是与固体内部某个点的变形状态有关的。设分别为固体中某个点的初始位置和变形后的位置。由u=[u,v,w]T定义了一个位置的向量场：xt=x0+u。该点的应变可以用位移的梯度场∇u来进行计算。令J代表由x0到tx映射的雅克比矩阵。采用线性的柯西-格林应变张量，可以将应变张量表示为：

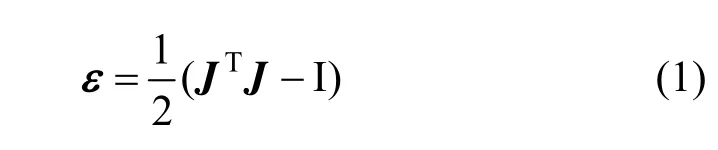
如果将固体近似考虑成线弹性各项同性材料，应力与应变张量的关系可以定义为：

对于各项同性材料，C是一个四阶各项同性张量[5]。

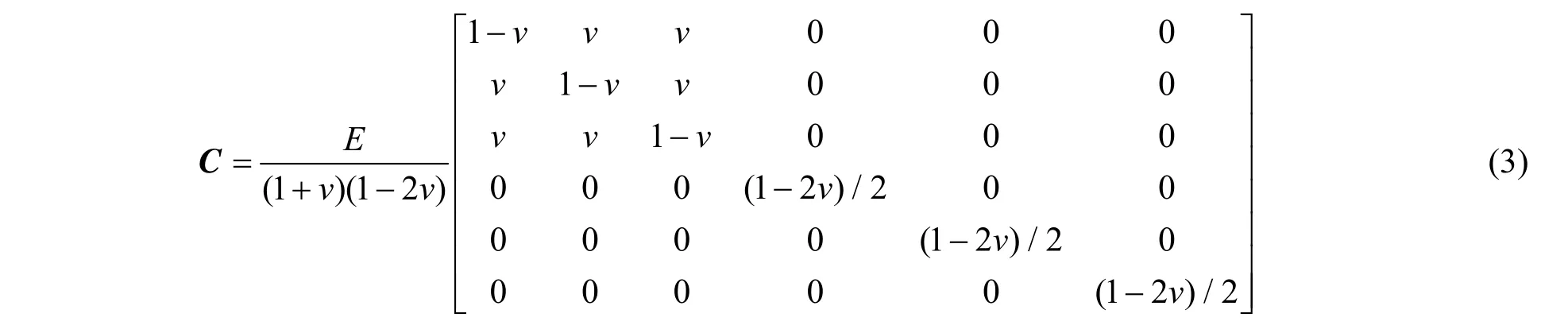
其中E与v分别是材料的弹性模量和泊松比。

2.3 SPH离散求解

SPH是一种无网格粒子法，最早用于天体物理现象的模拟[16]，此后广泛应用于流体力学和固体力学的数值分析中。在SPH中，每个粒子在连续的标量场f(x)的值是通过核近似法转化为支持域内所有离散的粒子数据的叠加来计算得到：

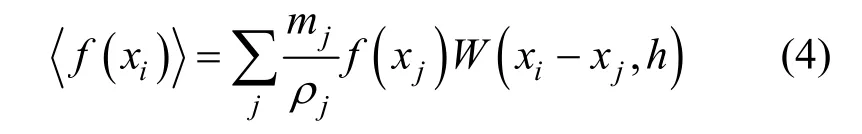
相关SPH的详细内容及公式推导可参见文献[15]。

通过使用SPH方法可以对2.2节中线弹性固体力学方程来进行离散求解，在2.1节中已经将计算区域离散成与四面体有关的粒子。因此，对固体内部的每个粒子，位移梯度场的SPH近似表达式为：

其中向量uji代表的邻接粒子uj与当前粒子iu的位移差：

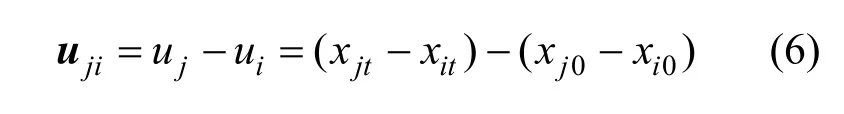
2.4 虚位移计算

采用上述SPH方法可以对固体在外力作用下所产生的内部应力进行分析。在模拟过程中，外力主要是由于固体间的相互碰撞产生的。因此首先要进行的是碰撞的处理。将刚体离散成一系列粒子之后，刚体间的碰撞检测实际上是由粒子来完成的。在模拟脆性破裂时，可将固体考虑成具有无限大刚性的刚体。为了能够使用2.2节的线弹性固体力学模型进行分析，需要为发生碰撞的固体粒子计算一个虚位移的状态来得到碰撞时发生的变形以此来计算应变和应力。对每个发生碰撞的粒子，本文使用粒子的碰撞信息来计算虚位移状态，如图2所示，碰撞粒子的虚位移的状态是由穿刺深度所决定的。当每个碰撞粒子的虚位移状态被确定之后，应力和应变张量就可以使用2.3节所述的公式进行计算。

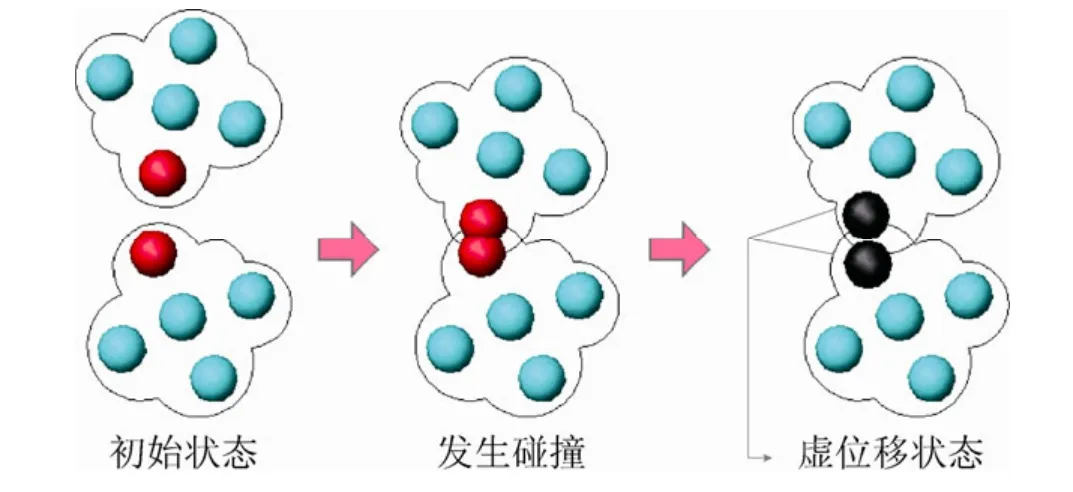
图2 碰撞粒子虚位移状态的确定，虚位移状态(黑色)是由碰撞的穿刺深度所决定

3 基于粒子细分的开裂处理

3.1 开裂准则

若将每个SPH粒子的所保存四面体顶点坐标作为内力分析的初始计算位置。当某个点的应力超出材料允许的值时就发生开裂现象。对于脆性破裂的模拟，本文采用经典的Rankine[17]条件：当固体内部某点应力σ的主应力所对应的特征值pmax超过了给定的材料阈值pm:pmax＞pm时，材料达到其破坏条件，裂缝由该点产生，初始开裂断面的法向为主应力的方向。裂缝的延伸通过引入了一个开裂半径的参数来模拟。

3.2 开裂断面的快速生成

第2.1节提出的固体的表面模型可以快速地进行开裂面的更新。当初始裂缝的位置和方向被确定之后，首先在以初始点为圆心，开裂半径的球体区域内进行查询，任何与开裂法相所在平面相交的“链接”都会被移除。与该链接相交的三角形将被加入到一个三角形集合中用来作为渲染的几何面。图3是二维下开裂断面处理的过程。

图3 二维下破裂计算与处理

使用上述方法生成的开裂面能够有效地维护几何拓扑关系并且生成开裂断面。但是，在模型初始离散的尺度较大的情况下其模拟的断裂面效果是较为粗糙的，并且对原始计算开裂面的逼近程度不够，然而如果提高初始模型的离散尺度又会增加系统的计算负担。为了解决这个问题，这里提出了一种粒子细化的模型来增强开裂细节。首先，在进行开裂处理之前，对所有属于移除“链接”的粒子进行标记。然后对每个标记的粒子，使用一种粒子细分方法将原始粒子进行分解以增强细节。

由于初始的每个粒子实际上是代表着一个四面体，因此，每个粒子细分后的粒子所代表的总四面体区域应该与初始四面体区域相等，粒子的细分实际上是对原有四面体区域进行细分。为了减少细分处理的复杂性，这里选择了一种较为统一的四面体细分计算模型，将每个需要细分的粒子分解成12个粒子。

首先，对于每个需要细分的粒子，在其所代表的四面体各边中点，将其分解为4个角的四面体和中心的一个八面体，对中心的八面体需要作进一步分割，一种普遍的方法是在八面体中插入一条对角线，使八面体分割成4个小四面体，如图4(a)～(b)。由于可选择的八面体对角线有两条，在实际细分时需要选择对角线进行操作，而如何选择对角线的标准不好确定。为了避免选择对角线的操作，本文使用一种新的细分操作，见图4(c)。对于每个八面体单元，在八面体的重心处(八面体6个顶点坐标的平均值)插入一个新的顶点, 然后将八面体原有的6个顶点与新顶点连接, 形成8个四面体，如图4(d)。

图4 一个八面体细分成四面体的算法

这样做的优点是每次划分一个四面体时只需要计算原四面体六条边的中点和形心，避免了分解方式的不确定性。图5是一个四面体分解的过程。首先将粒子所代表的四面体的各边中心分解为一个4个小四面体和一个八面体，再将八面体的分解为8个四面体，从而将原粒子细分为12个小粒子。在粒子细分完成之后再根据细分后的粒子进行开裂面的生成。图6是使用粒子细分进行开裂处理的过程。

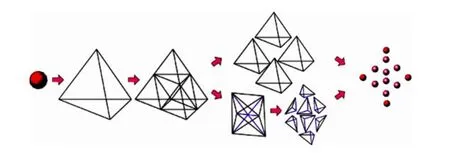
图5 单个粒子细分的过程

使用上述粒子细分的模型，仅仅需要在开裂处理时计算细分的粒子，因此对于模拟框架的整体计算效率影响不大，却又能得到细节较好的结果。

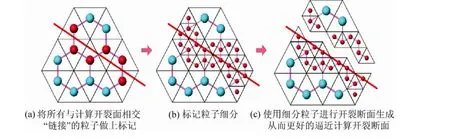
图6 二维下使用粒子细分进行开裂处理

综上所述，整个开裂模拟过程可以分成以下4个步骤：

(1) 进行刚体动力学计算和碰撞检测，发生碰撞时，使用SPH方法对所有粒子的坐标顶点进行应力分析。若某个点主应力所对应的特征值大于给出的材料参数值；将其加入到开裂点集合中。

(2) 对每个开裂点，在用户定义的开裂半径的区域内进行搜索，将与开裂断面相交的所有“链接”的粒子进行标记

(3) 对每个粒子进行细分处理，将细分后的粒子进行开裂断面的生成

(4) 根据粒子间关系来进行碎片的生成。

4 算法实现与结果分析

4.1 算法实现

图7是整个模拟算法的流程，在每个时间步长内，首先使用刚体动力学来模拟固体的运动。碰撞检测是基于固体表面粒子的，我们使K-D树进行碰撞检测的加速，碰撞反应采用了文献[18]中基于冲量的方法。分属于不同固体的表面粒子在发生碰撞时产生虚位移并使用SPH进行内力分析，将与计算开裂法相关的粒子进行细分后进行开裂断面的生成。

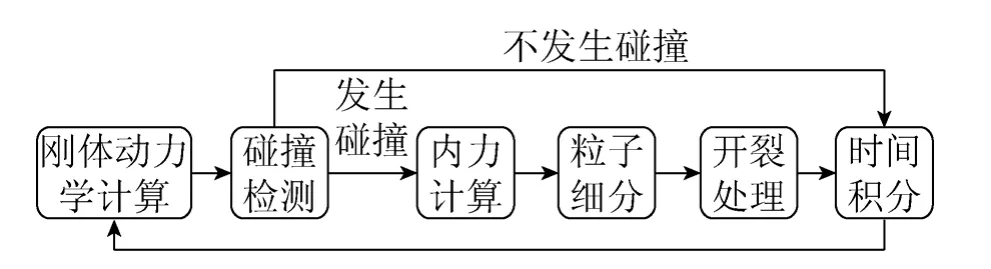
图7 整体框架算法流程图

以上方法在Intel (R) Core i3 2100 (R) 3.2 GHz CPU,4 GB 内存, NVIDIA GeForce GTX460 图形卡,1 GB显存的台式机上进行编程。使用Intel® TBB库进行了在CPU上的并行加速。模拟的结果采用V-Ray(www.chaosgroup.com)进行真实感渲染。

4.2 绘制结果与分析

图8是模拟9个下落的砖块在撞击地面产生的破裂效果，九个砖块从不同角度掉落地面，从而产生不同的破碎效果。图9是一个实心球撞击砖墙的模拟结果，图9(a)是不采用粒子细分算法和采用粒子细分算法进行开裂面生成的模拟结果，图9(b)是采用粒子细分算法进行开裂模拟的放大图，通过对比可以看出在采用粒子细分的算法进行开裂面生成对细节有明显的提高。而总的计算速度却没有大幅度下降，仅仅在进行断面生成时需要额外的计算时间。

表1是本文算法进行模拟的性能统计。表2是本文方法与相关文献方法的比较。文献[8]、[11]、[13]是近年来图形学领域中进行破碎模拟的几种典型方法。相对于文献[8]基于网格的有限元方法，由于采用了将四面体网格几何信息与形心粒子相结合的方法，本文方法在维护几何拓扑的效率上有优势。相对于同样使用粒子的MLS(文献[11])及MLPG(文献[13])方法，由于MLS及MLPG在内力分析时对邻接粒子位置的要求较高，因此离散时需要较小的粒子，而本文的数值方法是基于SPH，其数值稳定性较高，而且采用了细分粒子的方法，能够在较小的计算代价下得到更为丰富的细节，既保证计算效率，又不丢失细节。

图8 砖块落地破碎的模拟效果

图9 砖墙受冲击倒塌的模拟效果(左侧：使用原始粒子；右侧：使用细分粒子)

表1 不同实验的性能对比

表2 本文方法与相关文献方法的比较

5 总结与展望

本文提出了一种基于细分粒子的刚体破裂快速模拟算法。该算法具有如下特点：

(1) 该算法使用粒子固体进行离散建模。通过对每个碰撞粒子估计一个虚位移状态并使用来SPH方法对碰撞时产生的局部内力进行了分析求解，能有效地提高计算效率。

(2) 将固体四面体化后的网格绑定到粒子上，并提出一种细化粒子的算法来进行开裂面的生成，同时兼顾计算速度和模拟细节。

本文固体模型是基于粒子的，规则固体在进行碰撞时需要的检测的粒子数量较多，使之成为快速模拟的瓶颈，下一步可以考虑多尺度的粒子框架。

未来的工作包括：采用GPU技术加速计算，将模型扩展到塑形破裂的模拟，考虑更为复杂大型场景的模拟。

[1]Terzopoulos D, Platt J, Barr A, Fleischer K.Elastically deformable models [C]// Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques.Anaheim, California, USA, 1987: 205-214.

[2]Terzopoulos D, Fleischer K.Modeling inelastic deformation: viscolelasticity, plasticity, fracture [C]//Proceedings of the 15th Annual Conference on Computer Graphics, and Interactive Techniques.Atlanta, Georgia,USA, 1988: 269-278.

[3]Norton A, Turk G, Bacon B, Gerth J, Sweeney P.Animation of fracture by physical modeling [J].The Visual Computer, 1991, 7(4): 210-219.

[4]Smith J, Witkin A, Baraff D.Fast and controllable simulation of the shattering of brittle objects [J].Computer Graphics Forum, 2001, 20(2): 81-90.

[5]Fung Y C.A first course in continuum mechanics [M].Prentice-Hall, Englewood Cliffs, N.J, 1969: 10-15.

[6]O'Brien J F, Hodgins J K.Graphical modeling and animation of brittle fracture [C]// Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques.Los Angeles, California, USA,1999: 137-146.

[7]O'Brien J F, Bargteil A W, Hodgins J K.Graphical modeling and animation of ductile fracture [J].ACM Transactions on Graphics, 2002, 21(3): 291-294.

[8]Bao Zhaosheng, Hong J M, Teran J, Fedkiw R.Fracturing rigid materials [J].IEEE Transactions on Visualization and Computer Graphics, 2007, 13(2):370-378.

[9]Müller M, McMillan L, Dorsey J, Jagnow R.Real-time simulation of deformation and fracture of stiff materials [C]// Proceedings of the Eurographic Workshop on Computer Animation and Simulation.Manchester, UK, 2001: 113-124.

[10]Parker E G, O'Brien J F.Real-time deformation and fracture in a game environment [C]// Proceedings of the 2009 ACM SIGGRAPH/Eurographics Symposium on Computer Animation.New Orleans, Louisiana, USA,2009: 165-175.

[11]Pauly M, Keiser R, Adams B, Dutr´e P, Gross M, Guibas L J.Meshless animation of fracturing solids [J].ACM Transactions on Graphics , 2005, 24(3): 957-964.

[12]Liu Ning, He Xiaowei, Li Sheng, Wang Guoping.Meshless simulation of brittle fracture [J].Computer Animation and Virtual Worlds, 2011, 22(2-3): 115-124.

[13]Müller M, Teschner M, Gross M.Physically-based simulation of objects represented by surface meshes [C]// Proceedings of the Computer Graphics International, Hersonissos, Crete, Greece, 2004: 26-33.

[14]Molino N, Bao Zhaosheng, Fedkiw R.A virtual node algorithm for changingmesh topology during simulation [J].ACM Transactions on Graphics, 2004,23(3): 385-392.

[15]Cheng S W, Tamal Krishna D, Shewchuk J R.Delaunay mesh generation [M].Broken Sound Parkway NW: CRC Press, 2012: 410.

[16]Liu M B, Liu G R.Smoothed particle hydrodynamics(SPH): an overview and recent developments [J].Archives of Computational Methods in Engineering,2010, 17(1): 25-76.

[17]Rankine W J M.On the stability of loose earth [J].Philosophical Transactions of the Royal Society of London, 1857, 147: 9-27.

[18]Bender J.Impulse-based dynamic simulation in linear time [J].Computer Animation and Virtual Worlds, 2007,18(4-5): 225-233.