单纯空间相邻域及染色的研究

2014-03-21张士庆

图学学报 2014年5期

张士庆，张号

(1.辽宁工程技术大学机械工程学院，辽宁阜新123000；2.中国矿业大学银川学院，宁夏银川 750011；3.广东美的厨卫电器制造有限公司，广东佛山 528300)

在“3维度”空间里的一堆肥皂泡，两两相邻的最大数目是4。若要将其染色，须4+1个颜色。将它们映射到2维度面上，就是四色问题[1-2]；映射到更多维度空间，就是近、现代理论物理学家、天文学家关心的宇宙及多个平行宇宙的几何模型问题[3-4]。多维度空间问题超出了人类的感知能力、观察能力和想象能力，常用“抽象几何”去表达[5-6]。“实几何”在平面上得到充分的演绎，但在空间却遇到很大的障碍。其实，直观是问题的源泉，也是追求的终极目的——人们总是在用各种手段和方法将感知不到的事物转化为直观的表象。因此，本文采用计算机3D模拟，用丰富的色彩，用“投影降维”的方法，最大限度赋予它相对直观的分析研究，希望使复杂的空间问题一目了然。

为了方便阅读和分析，本文尽量采用传统符号表述，例如，O-X1,X2, …,Xn：表示笛卡尔直角坐标系；D：表示维度；S：表示圆球；1DS、2DS、3DS…：分别表示圆、二维度球面、三维度球面…；结构式1DS2D、2DS3D、3DS4D…：分别表示圆面(圆圈及内部，属于二维图形)、球体(二维度球面及内部，属于三维度图形)、三维度球体(三维度球面及内部，属于四维度图形)…；H2、H3：分别表示投影平面、投影超平面(三维欧氏空间作为投影面)；平面的上、下(或球面2DS、3DS的内、外)——即空间反演平面(或2DS、3DS)；同时又大量制作直观的计算机模拟空间彩色表象，帮助读者去理解语言无法准确表达又难以想象的空间关系。除特别需要，一般不再说明。

1 单纯空间

单纯空间定义：处处同质的空间。欧几里得空间、黎曼球面空间没有对大小、方向设定条件，空间内的每一个点(元素)的所有微分性质都相同。将欧几里得平直空间和黎曼球面扩张至无穷远界(注：从1维度到4维度分别是点、线、面、体)[7-9]，它们就没有实质区别，称为射影空间，见图1所示。欧几里得平直空间(注：黎曼球面空间的特殊情况：半径R=∞)和黎曼球面空间统一起来，称为单纯空间。

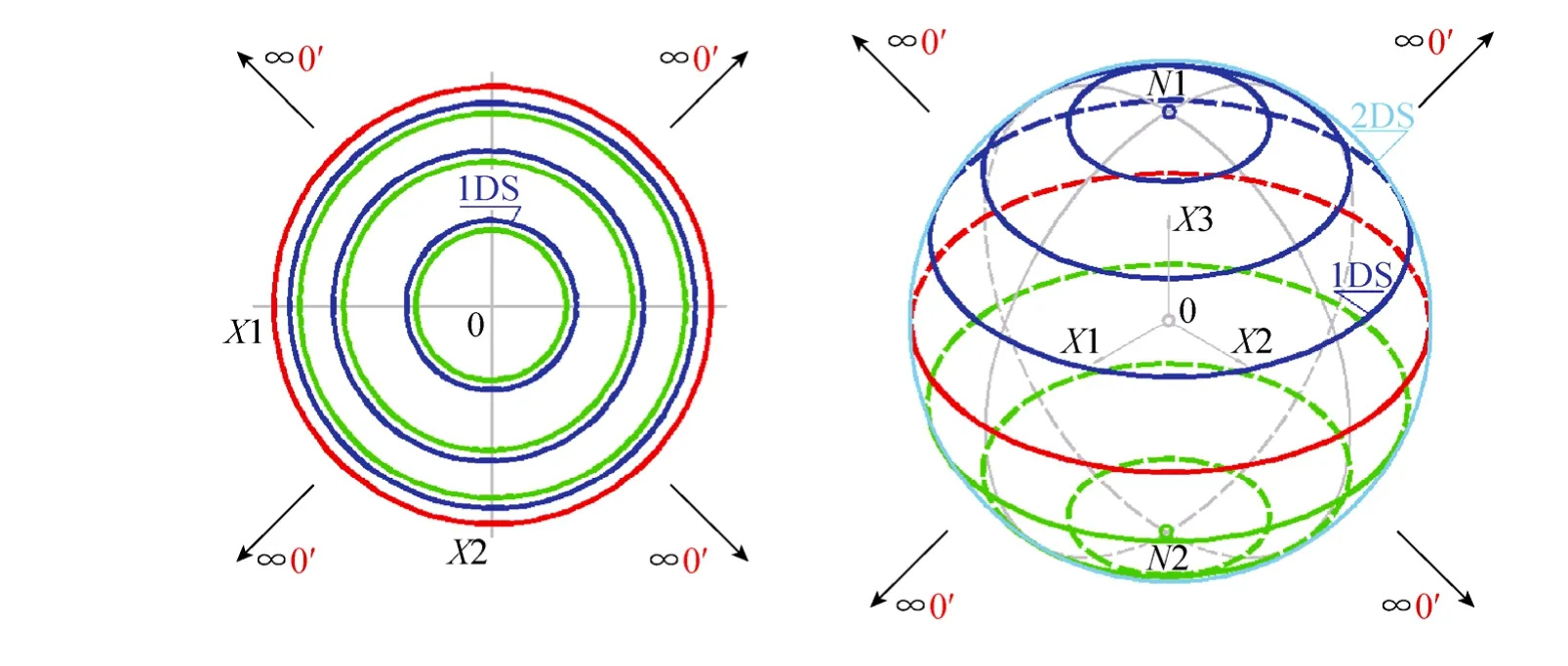
图1 单纯空间

本文定义“单纯空间”，是以直观的射影几何的方法去研究特殊的空间关系[9-10]，避免繁杂的几何体系以及抽象几何设定的假设、定理、公设，限制对实质问题的简洁讨论，也有利于对空间的两两相邻域、空间的N+1染色定理的研究。同时，也想与宇宙学“各向同性空间”一词建立某些联想，使它的应用扩展到诸如建立“标准宇宙”几何模型等类问题上。

本文讨论的问题仅限于单纯空间。多数情况下，“单纯空间”又特指有限的、具体的球面。

2 2DS3D相邻域实验

相邻域是指一个低维度空间将一个高维度空间一分为二，两者互为反演，拓扑等价[11]。例如平面上的一个圆，将平面分为内、外两个相邻部分；一个球面将空间分为内、外两个相邻部分(分别见图1左图、右图所示)。这两个相邻部分存在公共实质边界，称为两个相邻域，两者互为反演，拓扑等价。

2DS3D(球体)相邻域定义：两个及两个以上球体相交，球体彼此间有一个实质共有面，称其相邻(球面彼此间有一段实质共有线——表面交线)。

2DS3D(球体)两两相邻域定义：两个及两个以上球体相邻，且每个球体都与其它所有球体相邻，称其为两两相邻域(简称：相邻域)。

以上定义可以推广到更高维，词语相近。以下不再赘述。

在3DS空间，做2DS3D相邻域计算机模拟实验，将分析结果分类列表，如图2所示。上排图形(a)～(d)分别是无序的2DS3D球组合、四个有序的两两相邻的2DS3D球组合(以正四面体顶点为球心)、六个有序的2DS3D球组合(以正八面体顶点为球心)、八个有序的2DS3D球组合(以正六面体顶点——立方体顶点为球心)[12](注：图2(a)～(d)的上排图是实体造型渲染图，下排图是线网显示图)；图2(e)～(f)分别是4个有序的两两相邻的2DS3D球组合的结合过程、相邻域演变过程——随着白球变大，改变了红、蓝两球相邻域关系。

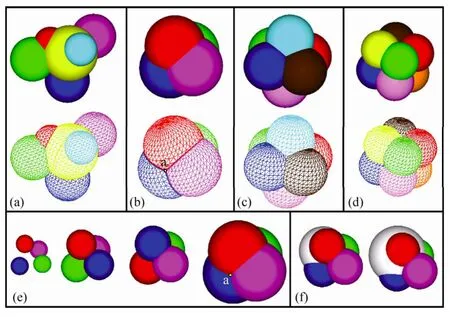
图2 2DS3D相邻域模拟实验图

两个球体相邻，有一条实质表面交线；3个球体两两相邻，彼此间有三段实质表面交线，并汇聚于一点，即图2(b)和图2(e)中a点处所示。实验表明两两相邻域最大数是4，即图2(b)和图2(e)所示。若加上背景空间，就是4+1。

3 2DS的映射分析法

设2D球面2DS，球心O，半径为r。以O为原点建立一个任意直角坐标系O-X1，X2，X3。设过球心，垂直于X3的平面为投影面H2，图3上排左图所示。球面上的所有平行于H2的圆，称为等高的纬线圆1DS。高度为l的等高的纬线圆1DS=f (r，l)。每个等高的纬线圆1DS正投影到H2上，就是反映自己实际形状的1DS圆。将它们都正投影到H2上，形成一个“二重圆域”，图3上排中图所示。上半球面投影到H2上表面(红线所示)，下半球投影到H2下表面(绿线所示)，得到图3上排右图所示正投影图形。这是一一对应的射影变换。由于是正投影，保留了水平部分的度量性。球面2DS与平面H2建立起映射关系。2DS和H2平面上的图形互为映射关系。图3下排图所示，由P向射影，球面上的红、绿、蓝3个两两相邻域图形与H2上的红、绿、蓝3个两两相邻域图形构成一一对应的映射关系。可以由H2平面上的这个图形去分析2DS球面上的图形，这一方法称为映射分析法(或投影降维分析法)。

图3 映射分析法

4 2DS3D两两相邻域最大数4+1

图4上排左图表明平面上的两两相邻域最大数是3+1，在文献[2]中已经作了严格证明。

图4上排右图是2DS3D及3DS(空间)的两两相邻域的几何证明图。2DS上与H2上的相邻域图是互为映射关系，因此只能在2DS(图中紫色的2DSⅡ)球面上，由三个两两相邻域图Ⅰ、Ⅲ、Ⅳ向外(或内——内、外无实质区别)空间做3个球体(图4下排左图、中图红、绿、蓝3球所示)；构成4个2DS3D两两相邻域：2DSⅠ(红色球)、2DSⅢ(绿色球)、2DSⅣ(蓝色球)及2DSⅡ(紫色的基础球)。这恰好与实验结果一致。假设有第5个2DS3D与这4个2DS3D都相邻，因为3个球体两两相邻，彼此间有3段实质表面交线，并汇聚于1点，因此这第5个2DS3D表面与2DSⅡ(紫色球面)的交线必须与紫线(2DSⅠ与2DSⅡ交线)、绿线(2DSⅢ与2DSⅡ交线)、蓝线(2DSⅣ与2DSⅡ交线)均有交点(图3下排图及图4所示)，这是不可能的。详细论证参见文献[2]。

图4 两两相邻域

传统意义平面上的两两相邻域问题，表面上是平面问题，实质是3D射影空间内的2维度平面问题。因为，没有3D射影空间，就不存在2DS变换问题；同时，人也无法去观察、分析2维度平面问题。平面上的两两相邻域最大数是“3+1”，其中“3”是指平面上最多只能做出3个都与背景平面(空间)相邻的两两相邻的2维度图形(图4上排左图所示)；“+1”是指2维度的背景平面(因为2维度图形不可能无穷大)。

空间中由4个2DS3D构成的两两相邻域的3维度图形(模型)，是4D射影空间内的3维度空间问题，实际两两相邻域最大数是4+1，其中“+1”是指3维度的背景空间。

图4下排右图，2DSⅠ、2DSⅡ、2DSⅢ、2DSⅣ是4个2DS3D构成的两两相邻域在H2上的投影示意图，2DSⅤ是背景空间。

5 三维球面的可视模型

图5上排图是在3DS空间的2DS投影降维法。图5下排图是在4DS空间的3DS一次投影降维。与3DS空间的2DS投影降维法相似，设过4DS空间的3DS球心O为原点，建立一个任意直角坐标系O-X1，X2，X3，γ(注:γ即X4)，以绝对垂直于γ的超平面为投影超平面H3[13]，图5下排左图所示(注：目前还没有制作4维轴测图的公认的理论、方法和技术)。3DS球面上，所有平行于H3的2DS(圆球面)称为等高的纬面圆球2DS(图上仅画出上、中、下三个2DS，中间大的2DS是3DS球面在H3上的截影)。在半径为R的3DS球面上，距离H3高度为L的等高的纬面圆球2DS=f (L，R)。每个等高的纬面圆球2DS正投影到H3上，就是反映自己实际形状的2DS球面。将它们都正投影到H3上，形成一个“二重圆球体域”。它的结构是：由以球心向外，一层一层2DS球面所构成，图5下排中图(正视)、右图(侧视)所示(前、上面剖去1/8，以便观看)；第4维γ，投影为一个点，即球心；上半3DS球面投影到H3“上表面”上(上、下、内、外无实质区别)——各球面彩色外壳所示，下半3DS球面投影到H3“下表面”上——各球面灰色内面所示。这是一一对应的射影变换，由于是正投影，保留了水平部分的度量性。3DS球面与超平面H3建立起映射关系。3DS上的图形映射到H3超平面上，形成一一对应的图形。可以由H3超平面上的这个图形去分析3DS球面上的图形。

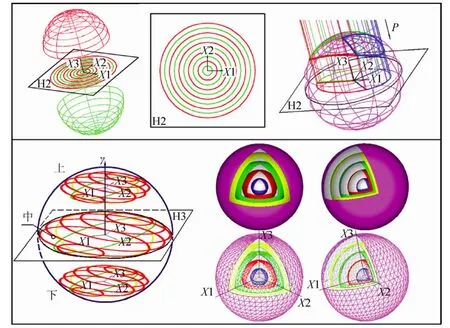
图5 三维球面及其投影模型

6 N维空间两两相邻域最大数定理

单纯空间两两相邻域最大数定理：在N维度单纯空间，做出N-1维度的两两相邻单纯空间的最大数是N+1，N+1之“+1”指的是背景空间。简称相邻域定理。证明如下：

由“4 2DS3D两两相邻域最大数4+1”所证：在3维度射影空间可以在2维度球面(或平面)上做出最多3个都与背景球面相邻的两两相邻的2维度图形(封闭线确定的面积，即1DS2D)，形成3+1个两两相邻的2维度图形(其中之一是背景图形，图3下排图、图4上排图所示)；将其映射到4维度射影空间，由上述3+1个具有2维度的1DS2D两两相邻域图形为基础，可以做出最多4个都与背景球面相邻的3维度两两相邻的2DS3D图形(封闭球面确定的体积)，形成4+1个两两相邻的3维度图形(其中之一是背景图形，图4下排图所示)。……按照由低维度到高维度构成的一一对应的射影变换，映射到更高维度空间，可以归纳为：设N-1(注：N≥5)维度射影空间成立，即：在其内部可以建立最多N-1个(N-2)维度两两相邻域球面图形，其两两相邻域最大数是[(N-1)+1]，[(N-1)+1]之“(N-1)”是相邻域球面图形数，其中“+1”是背景空间(因为球面图形不可能无穷大)；由一一对应的射影变换及一一对应的映射关系，将其映射到N维度射影空间中，由上述[(N-1)+1]个(N-2)维度两两相邻域球面图形为基础，可以做出最多[(N-1)+1]个都与背景球面(空间)相邻的(N-1)维度两两相邻域球面图形，形成[(N-1)+1]+1个两两相邻的(N-1)维度图形，两两相邻单纯空间的最大数是“[(N-1)+1]+1”，“[(N-1)+1]+1”之“[(N-1)+1]”是相邻域球面图形数，其中“+1”是背景空间(因为球面图形不可能无穷大)。即是：在N维度单纯空间，做出N-1维度的两两相邻单纯空间的最大数是N+1，N+1之“+1”指的是背景空间。

证毕。

二维度空间仅仅是传统概念意义上的特例。将它作为射影空间，即为1DS2D，内部的单纯空间是0DS1D，仅仅存在线束。相邻域问题，可以理解为点分线为两相邻部分(见图7)。

在上述这个几何体系下，我们所生活的空间(现实空间)，其实是在4维度射影空间中的3DS空间内。关于第4维γ(注:γ即X4)，除抽象几何(也称综合几何)外，即使是顶级学者也知之甚少，但他们越来越关心第4维γ，更越来越感到第4维γ存在的重要性，只是感知、观察和想象非常模糊。

7 N维空间(N-1)DS的构形图及N+1染色定理

设N维度单纯空间内，由若干个(N-1)DS任意分布，组合成一幅N-1维度构形图。其中每个(N-1)DS的结构式是：(N-2)DS(N-1)D，即由(N-2)维度球面及内部所构成的球体。

单纯空间N+1染色定理：在N维度单纯空间的每一幅N-1维度构形图，可以至多用N+1种颜色染色。简称N+1色定理。证明如下：

要区分相邻域就须染色，即相邻域染上不同颜色。

N维空间的(N-1)DS的构形图可以归纳为3种基本类型：①链式(图6左1所示)、②内含式(图6左2所示)、③两两相邻域式(图6左3所示)。如图6所示，是3DS空间的2DS邻域关系的3种基本类型。将3种基本类型的最简模型作为基本构形图，任意组合，可以生成任意复杂的构形图。例如：平面图形(地图)；空间的肥皂泡；超弦理论之多个“平行宇宙”的几何模型图。其构图的方法及过程都与地图相同[2]。

图6 基本构形图及染色定理

图6所示2DS的①链式、②内含式染色所需颜色数不多于③两两相邻域式；在N维度单纯空间依然如此。因此按照两两相邻域形式的基本构形图去作任意复杂的构形图，是研究染色所需最多颜色的充要条件。

设有一个含N+1个(N-1)DS组成的最大数两两相邻域构形图，染色所需颜色数为N+1。在以它为基本构形图的基础上，任意添加1域(即“第N+2域”，例如，图6右图白色球所示)；整个N+2个(N-1)DS构形图，超过两两相邻域最大数，必至少有2个(N-1)DS不相邻；这2个不相邻的(N-1)DS球，用同1种颜色染色。再任意添加1域“第N+3域”，当不改变原来各相邻域关系情况下，至多与其他N+2个域之中的N个(N-1)DS构形图组成两两相邻域，可以用这N个两两相邻域颜色之外的第N+1色染色；当改变原来各相邻域关系情况下(例如，与多于N+1个(N-1)DS相邻)，必出现①链式、②内含式结构，含有①链式、②内含式结构的N+2个(N-1)DS构形图可以染色，余下的最后一域，至多与其他N+2个域之中的N个(N-1)DS构形图组成两两相邻域，因此可以用这N个两两相邻域颜色之外的第N+1色染色。设N+T个(N-1)DS构形图可染(注：T≥3，整数)，再任意添加1域“第N+T+1域”，构成N+T+1个(N-1)DS构型图，当不改变原来各相邻域关系情况下，“第N+T+1域”至多与其他N+T域之中的N个(N-1)DS构形图组成两两相邻域，可以用这N个相邻域颜色之外的第N+1色染色；当改变原来各相邻域关系情况下，必出现①链式、②内含式结构，按照上述推理，含有①链式、②内含式结构的N+T个(N-1)DS构形图可以染色，则余下的最后一域，至多与其他N+T域之中的N个(N-1)DS构形图组成两两相邻域，因此可以用这N个相邻域颜色之外的第N+1色染色。即是：在N维度单纯空间的每一幅N-1维度构形图，可以至多用N+1种颜色染色。

证毕。

这一论证过程在文献[2]中已经用过。图6右图是3DS空间中的2DS例，在N维空间中的(N-1)DS也类似。

N+1染色定理适用于从特例1DS2D到(N-1)DSND的所有情况。例如：1DS2D，即2维度(平面)射影空间，其内部的构形图结构式是0DS1D，0DS表示无单纯空间构形图，1D表示仅仅存在线束，点分线为两相邻部分，染色须3色(图7左图所示)；2DS3D，即3维度射影空间，其内部的构形图结构式是1DS2D，表示圆面构形图，就是“四色问题”(图7中图所示)；3DS4D，即4维度射影空间，其内部的构形图结构式是2DS3D，表示球体构形图，就是“肥皂泡问题”(即现实空间)，染色须5色(图7右图所示)。

图7 染色图例

8 标准宇宙的三维投影模型

几何学的产生、发展都是为了应用。上述内容的另一个重要应用是可以为理论物理学、宇宙学提供一个有坚实几何学基础的标准宇宙的3维度投影模型[14-17]。如图8所示，从左至右分别是4DS空间3DS示意图(两团色斑表示两个有限宇宙)、无限宇宙在H3(超平面)上的3维度投影模型(图8左2所示)、有限并行宇宙在H3(超平面)上的3维度投影模型(图8左3所示)、有限相邻宇宙在H3(超平面)上的3维度投影模型(图8左4所示)。

图8 标准宇宙的三维投影模型

基于这一模型，可以用重积分方法计算宇宙容量I(参见文献[14])：

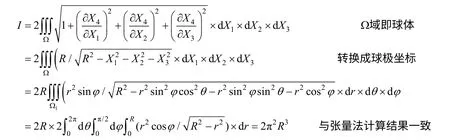
宇宙的年龄约140亿年，具体容量还没有定论。若宇宙范围(测地线周长)L=1250亿光年，则R=L/2π≈200亿光年，I≈15.8×1031[光年]3；则径向膨胀速度超光速，周向退行速度大于3倍光速；则“视界”仅为宇宙的1/3。若宇宙范围L=280亿光年，则地球处于A点，恰好可以从两个相反方向看到最远点B，图8右图所示。若宇宙范围＜280亿光年，则可以从两个相反方向看到不同时期的点C。存在膨胀因素的影响，实际情况很复杂[14,17]。

9 结束语

“实几何”对空间问题的研究十分重要。一些世界难题，例如，四色问题，空间相邻域及染色问题，经过“实几何”，借助计算机辅助研究，会变得一目了然。

空间——宇宙，既是科学问题，也是哲学问题，自古以来受人关注。人类太渺小，只是近代才对宇宙有一些肤浅认识。但近一百年来有加速认识的动力、方法和手段。发展趋势之一是不断突破对空间的认知。在纯数学、理论物理学、宇宙观测得到突飞猛进发展之时，“实几何学”却没有长足进步，以至于完成这篇论文十分困难；而且仍然有缺憾之处，这些缺憾之处是在近期无法解决的世界难题(例如，4D模拟的理论、方法、技术)。作此论文，除论证以上问题，也想关注实几何问题、空间关系问题与现代科学技术的紧密联系。

[1]百度百科.四色定理[EB/OL].http://baike.baidu.com/view/43945/htm, 2012-02-10.

[2]张士庆, 张号.四色问题的直观几何论证及单纯性地图四色定理[J].图学学报, 2013, 5(34): 45-50.

[3]Binney J, Merrifield M.星系天文学[M].赵刚, 译.北京: 中国科学技术出版社, 2004: 395-452.

[4]英格利斯 S J.行星恒星星系[M].北京: 科学出版社,1979: 458, 460-466.

[5]罗淼, 严虹, 廖义琴.几何学概论[M].北京: 清华大学出版社, 2011: 241-266.

[6]费里波夫 ПВ.多维空间画法几何及其应用[M].谢申鑑, 周积义, 译.北京: 清华大学出版社, 1983: 7-16,133-156.

[7]周建伟.微分几何讲义[M].北京: 科学出版社, 2010:1-16.

[8]苏步青, 胡和生, 沈纯理, 张国粱.微分几何[M].北京: 人民教育出版社, 1976: 212-221, 230-233.

[9]梅向明, 刘増贤, 林向岩.高等几何[M].北京: 高等教育出版社, 1983: 17-20, 36-44, 231-246, 265-272.

[10]胡国权.几何与代数导引[M].北京: 科学出版社,2006: 313-323.

[11]龙泽斌.几何变换[M].长沙: 湖南科学技术出版社,1984: 273-281, 293-298, 98-99.

[12]希尔伯特 D.直观几何[M].王联芳, 译.北京: 高等教育出版社, 1964: 92-95, 144-161, 217-232, 330-338.