标准Ⅱ型马蹄形断面水跃共轭水深的简化计算
2014-03-27张志昌贾斌
张志昌, 贾斌
(西安理工大学 水利水电学院,陕西 西安 710048)
马蹄形断面是由底部的弓形、下部两侧的扇形以及顶拱半圆形组成的。由于断面形式复杂,近几年来学者们采用不同的方法研究了马蹄形断面的正常水深和临界水深,这些研究成果都以迭代或优化拟合方法进行表述。文献[1]给出了标准Ⅱ型马蹄形断面Q2/r5<26.131 3和Q2/r5>26.131 3两种情况下临界水深的迭代公式;文献[2]给出了标准Ⅰ型和标准Ⅱ型马蹄形断面临界水深的迭代公式。文献[3]给出的临界水深的计算公式较为复杂;文献[4]通过迭代和逐步优化拟合,给出了马蹄形断面临界水深的直接计算方法;文献[5]认为马蹄形断面的底拱一般为半径很大的圆,可将其视为平底,给出了这种情况下临界水深的计算方法。文献[6]通过对马蹄形断面临界流方程的数学变换,应用逐步优化拟合原理,得到马蹄形断面临界水深的直接计算式。文献[7]引入准一次函数、准二次函数的概念,给出了计算马蹄形两种标准断面正常水深的简化公式。文献[8]引入无量纲参数得到了平底II型马蹄形断面正常水深和临界水深的直接计算公式。文献[9]研究了标准Ⅱ型马蹄形断面正常水深、弗劳德数和收缩断面水深的计算方法。
对水跃水力特性的研究已有一百多年的历史,但主要是针对矩形断面[10]。
对于马蹄型断面水跃的研究,文献[11]给出了平底马蹄形断面(一般马蹄形断面底部为弓形,平底是特殊形式)的水跃计算方法,该方法给出了压力项的积分结果,但未给出被积函数的表达形式,文献[11]还给出了马蹄形输水管道共轭水深的计算曲线以供查用,但查图法精度较低。文献[12]研究了标准Ⅰ型马蹄形断面水跃的共轭水深,但在计算中仍采用试算法,计算比较麻烦。
马蹄形断面成洞比较容易,抗压能力强,对围堰的适用性较好,是工程中常用的断面形式,水跃共轭水深的计算对工程应用十分重要,但目前尚未看到计算标准Ⅱ型马蹄形断面水跃共轭水深方面的论文,因此本研究应用水跃的基本方程,研究标准Ⅱ型马蹄形断面水跃共轭水深的一般计算方法和简化计算方法,供设计参考。
1 标准Ⅱ型马蹄形断面的面积和形心距水面距离的计算
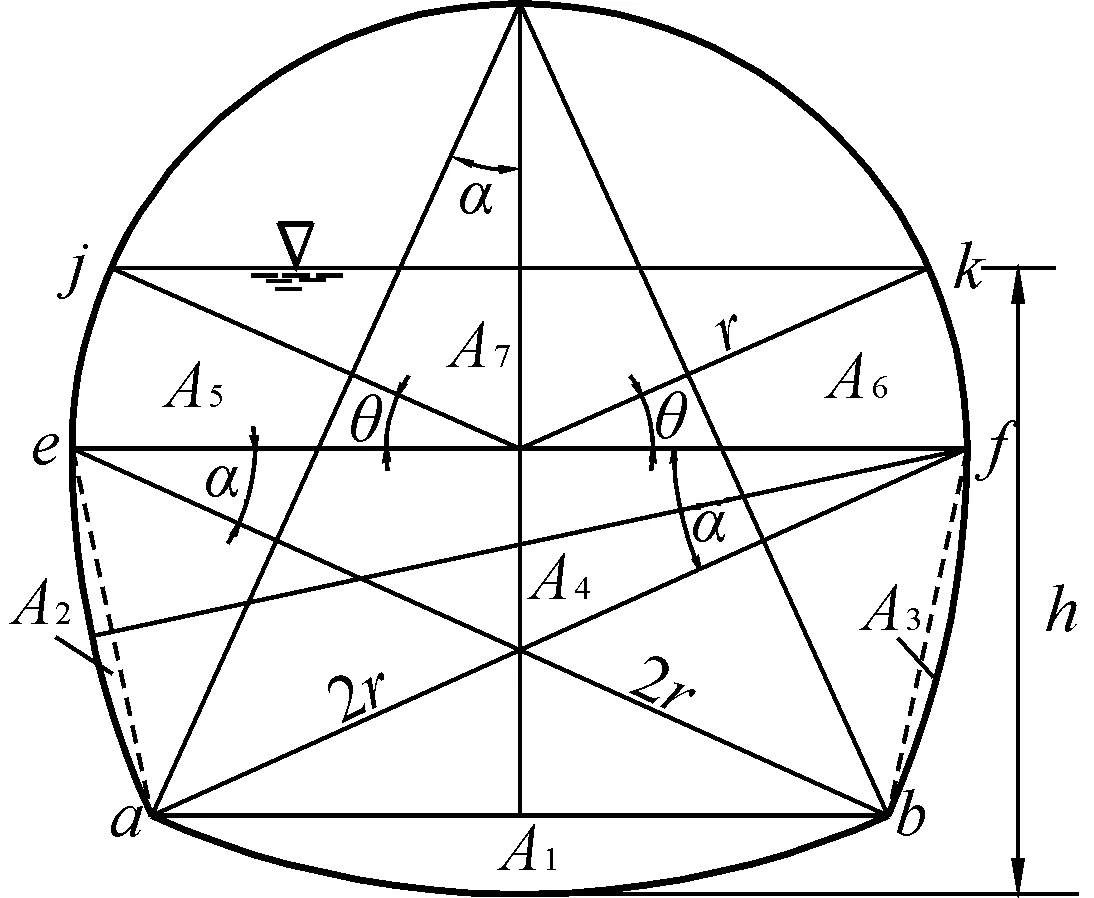
标准Ⅱ型马蹄形断面如图1所示,由ab线以下,圆心角为2α的底部弓形断面;ef线与ab线之间,圆心角为α的圆弧段和ef线以上的半圆形组成。ef线以下三圆弧段的半径均为2r,ef线以上顶拱半径为r,α=24.29519°。

图1 标准Ⅱ型马蹄形断面
1.1 当水深处于底部弓形断面时(图2中的ab线以下(含ab线))
如图2所示,水深处于底部弓形断面的断面面积和形心距水面的距离为:
A=(2r)2(2φ-sin2φ)/2=
2r2(2φ-sin2φ)
(1)
(2)
式(1)和(2)中,φ为当水深为h时对应的半圆心角。
弓形断面的水深为:
h=2r(1-cosφ)
(3)
式(3)中,0<φ≤24.29519°,0 图2 水深处于底部弓形断面内 如图3所示,将图中的几何图形分为4部分,即底部的弓形面积A1、两侧的弓形面积A2、A3和中间的梯形面积A4。 图3 水深处于最大直径(含最大直径)断面内 分别计算各块的面积和形心距水面的距离,根据叠加原理求出面积和,而断面形心距水面的距离计算[13]为: (4) 式(4)中,yc1、yc2、yc3、yc4分别为底部弓形断面、两侧的弓形断面和中间的梯形断面形心距水面的距离。略去繁琐的推导过程,得断面面积和形心距水面的距离为: A=r2{0.196124152+4[(α-β)-sin(α-β)]+ (2sinα+2cosβ-1)(2cosα-1-2sinβ)} (5) (6) 式中, 水深为: h=r(1-2sinβ) (7) 式中,0<β≤24.29519°,0 如图4所示,将断面面积分为7部分,即底部的弓形断面面积A1、两侧的弓形面积A2和A3、中间的梯形面积A4、ef线以上的扇形断面面积A5和A6以及三角形面积A7。 由图4可得断面面积为: A=r2(1.746496972+θ+sinθcosθ) (8) 断面形心距水面的距离为: hc=r[0.793418211+1.746496972sinθ+ θsinθ-(4/3)sin2(θ/2)+ (1/3)sin2θcosθ]/ (1.746496972+θ+sinθcosθ) (9) 水深为: h=r(1+sinθ) (10) 式中,0<θ<90°,0 图4 水深位于最大直径以上断面 水跃共轭水深是基于动量方程推导出来的,其计算公式为[14]: (11) 式(11)可以写成: J(h1)=J(h2) (12) 式中,A1、A2分别为跃前和跃后断面面积;hc1、hc2分别为跃前和跃后断面形心到水面的距离;Q为流量;g为重力加速度。 马蹄形断面水跃方程的计算比较复杂,水深处于断面不同位置时有不同的计算公式,可能有多种组合形式,如表1所示。在计算时根据不同的组合形式,选择相应的计算公式。 表1 不同工况下共轭水深的计算公式 水跃计算可以用试算法,如果已知跃前或跃后断面水深,根据相应公式计算出断面面积和形心距水面的距离,求得J(h1)或J(h2),代入公式(11),试算求解另一个断面的水深。 由以上推导过程可以看出,除了水深处于底部弓形断面内时断面面积和形心计算比较简单,当水深处于底部弓形断面以上时,马蹄形断面水跃共轭水深的计算十分复杂,计算工作量大。为了简化计算,根据上面得到的面积公式(1)、(5)、(8)和形心公式(2)、(6)、(9)分析了相对面积、相对形心与相对水深的关系,见图5和图6,根据最小二乘法原理,得到经验公式,为: 当0.01 A/r2=2.5078(h/r)1.4812 (13) hc/r=0.407(h/r)1.0051 (14) 公式(13)的平均误差为1.1%,最大误差为2.24%;公式(14)的平均误差为0.54%,最大误差为2.23%。 当0.27 A/r2=-0.3051(h/r)3+0.8324(h/r)2+ 1.265(h/r)-0.0411 (15) hc/r=0.0487(h/r)3-0.1042(h/r)2+ 0.5385(h/r)-0.0298 (16) 公式(15)的平均误差为0.276%,最大误差为0.836%;公式(16)的平均误差为0.246%,最大误差为2.0%。 图5 相对面积与相对水深关系 图6 相对形心与相对水深关系 为了进一步简化计算,分析了Ahc/r3与h/r的关系,见图7。 图7 Ahc/r3与h/r的关系 分段拟合结果如下。 当0.01 Ahc/r3=1.036(h/r)2.4915 (17) 当0.27 Ahc/r3=-0.0192(h/r)3+1.0127(h/r)2- 0.2228(h/r)+0.0268 (18) 公式(17)的平均误差为0.393%,最大误差为1.07%;公式(18)的平均误差为0.4236%,最大误差为1.64%。 水跃公式(11)可以改写成式(19)或式(20)的形式。 (19) J(h1/r)=J(h2/r) (20) 对于跃前和跃后水深均在0.01 如果知道跃前断面水深h1,可由公式(13)和(14)或公式(15)和(16)计算出A1/r2和hc1/r,代入公式(20)计算出跃前断面的J(h1/r),将公式(15)和(18)代入公式(19)得跃后断面相对水深的迭代式为: (21) 式中, M=gr5[(-0.3051)(h2/r)3+0.8324(h2/r)2+ 1.265(h2/r)-0.0411] 如果已知跃后水深h2,则可由公式(20)计算出J(h2/r),跃前断面相对水深的迭代公式为: (22) 式中, N=g{J(h2/r)-r5[-0.0192(h1/r)3+ 1.0127(h1/r)2-0.2228(h1/r)+0.0268]} 例题1标准Ⅱ型马蹄形断面,已知顶拱半径r=5 m,渠道过流量Q=290 m3/s,跃前水深h1=2.5 m,试判断是否会发生水跃,若发生水跃,试计算跃后水深。 1)试算法 底部弓形断面高度为: h0=2r(1-cosα)= 2×5×(1-cos24.29519°)=0.8856 m 因为h0 β=arcsin(0.5-0.5×h/r)= arcsin(0.5-0.5×2.5/5)= 14.4775° 将α=24.29519°,β=14.4775°,r=5代入公式(5)得断面面积A=19.18827 m2。将α、β、r代入公式(6)中计算有关参数为C=9.659165,D=0.068,E=11.216505。 跃前断面的总形心为: 临界水深可以用来判断渠道是否会发生水跃,只有当跃前断面水深小于临界水深才能发生水跃。对于临界水深用笔者的公式计算,当0.037956 hk=0.7536[Q2/(gr5)]0.2856r= 0.7536×2.746120.2856×5= 5.0282 m 因为跃前断面水深小于临界水深,所以在渠道中发生水跃。 跃后水深假定在图1中的ef线以上,计算时假设一个θ,用公式(8)、(9)、(10)计算跃后断面面积、形心高度和跃后水深,由公式(11)试算结果为θ=55.93°,A2=79.6677 m2,hc2=4.52453 m,h2=9.142 m。 2)简化公式计算 已知h1=2.5 m,hk=5.0282 m,渠道中发生水跃。因为h1/r=2.5/5=0.5,所以跃后水深一定在0.27 跃后水深用公式(21)求解,将J(h1/r)=11790.712代入迭代得h2/r=1.836677,h2=9.1834 m。与理论公式计算的9.142 m相差了0.475%。 例题2某标准Ⅱ型马蹄形断面,已知半径r=1.5 m,渠道过流量Q=14.079 m3/s,跃后水深h2=2.5 m,求跃前水深。 解:0.27 将J(h2/r)=24.88754796,Q=14.079 m3/s,r=1.5 m代入公式(22)迭代得h1/r=0.5572,h1=0.8358 m。 用理论公式计算,求得J(h2)=11.0726,代入理论公式(11)试算得β=12.911°,跃前水深为0.83 m,简化公式误差为0.7%。 1)根据标准Ⅱ型马蹄形断面的几何形状,研究了断面面积和面积形心的计算方法; 2)根据水跃的基本方程,研究了水跃共轭水深的一般计算方法和简化计算方法; 3)简化计算方法简单、实用、容易掌握,通过算例证明简化计算方法的计算精度完全满足工程设计要求。 参考文献: [1] 李永刚. 马蹄形隧洞水力计算迭代法[J]. 人民黄河,1955,11:42-44. Li Yonggang. Iterative method of horseshoe tunnel hydraulic calculation[J]. Yellow River, 1995,11:42-44. [2] 吕宏兴.马蹄形过水断面临界水深的迭代计算[J].长江科学院院报,2002,19(3):12-14. Lü Hongxing. Calculation on critical depth of horseshoe cross-section by iterative method[J].Journal of Yangtze River Scientific Research Institute,2002,19(3):12-14. [3] 谭新莉. 马蹄形断面水力学计算[J]. 新疆水利,2003,2:20-23. Tan Xinli. Hydraulic calculation of horseshoe-shaped section[J].Xinjiang Water Resources,2003,2:20-23. [4] 王正中,陈涛,芦琴,等. 马蹄形断面隧洞临界水深的直接计算[J]. 水力发电学报,2005,24(5):95-98. Wang Zhengzhong, Chen Tao, LU Qin, et al. The direct solution on critical depth of horseshoe section tunnel[J]. Journal of Hydroelectric Engineering,2005,24(5):95-98. [5] 马吉明,梁海波,梁元博. 城门洞形及马蹄形过水隧洞的临界水流[J]. 清华大学学报,1999,39(11):32-34. Ma Jiming, Liang Haibo, Liang Yuanbo. Critical flow in City-Gate and horseshoe conduit[J]. Journal of Tsinghua University,1999,39(11):32-34. [6] 张宽地,吕宏兴,陈俊英.马蹄形过水断面临界水深的直接计算法[J].农业工程学报,2009,25(4):15-18. Zhang Kuandi, Lü Hongxing, Chenjunying. Direct calculation of critical depth of horseshoe section tunnel[J].Transactions of the CSAE,2009,25(4):15-18. [7] 赵延风,王正中,芦 琴.马蹄形断面正常水深的直接计算公式[J]. 水力发电学报,2012,31(1):173-177. Zhao Yanfeng, Wang Zhengzhong, Lu Qin. Direct calculation formulae for normal depth of horseshoe section [J].Journal of Hydroelectric Engineering,2012,31(1):173-177. [8] 文辉,李风玲.平底马蹄形断面的水力计算[J].农业工程学报,2013,29(10):130-134. Wen Hui, Li Fengling. Hydraulic calculation of horseshoe cross-section with flat-bottom[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(10): 130-135. [9] 张志昌,李若冰.标准Ⅰ型马蹄形断面水力特性的研究[J]. 长江科学院院报,2013,30(5):55-59. Zhang Zhi chang,Li Ruobing. Hydraulic characteristics of standard I-Type horseshoe cross section[J].Journal of Yangtze River Scientific Research Institute,2013,30(5):55-59. [10] 张志昌,李若冰,赵莹,等.综合式消力池深度和坎高的计算[J].西安理工大学学报,2013,29(1):81-85. Zhang Zhichang,Li Ruobing,Zhao Ying,et al. Calculation of the depth of comprehensive stilling basin and the height of ridge[J]. Journal of Xi 'an Polytechnic University ,2013,29(1):81-85. [11] 马吉明,谢省宗,梁元博. 城门洞形及马蹄形输入隧洞内的水跃[J]. 水利学报,2000,7:20-24. Ma Jiming,Xie Shengzong,Liang Yuanbo,Hydraulic jumps in rectangular conduit with circular upper wall and horseshoe tunnel[J].Journal of Hydraulic Engineering,2000,7:20-24. [12] 李若冰,张志昌. 标准Ⅰ型马蹄形断面水跃共轭水深的计算[J].西北农林科技大学学报,2012,40(8):230-234. Li Ruobing, Zhang Zhichang. Hydraulic characteristics of standard I-Type horseshoe cross section[J].Journal of Yangtze River Scientific Research Institute, 2012,40(8):230-234. [13] 单辉祖. 材料力学教程[M]. 北京:高等教育出版社,2007:321-340. [14] 张志昌. 水力学(下册)[M]. 北京:中国水利水电出版社,2011:69-90.
1.2 水深处于最大直径以下(含最大直径)的断面时(图3中的ef线以下)

1.3 水深处于最大直径以上的断面时(图4中的ef线以上)
2 共轭水深的计算

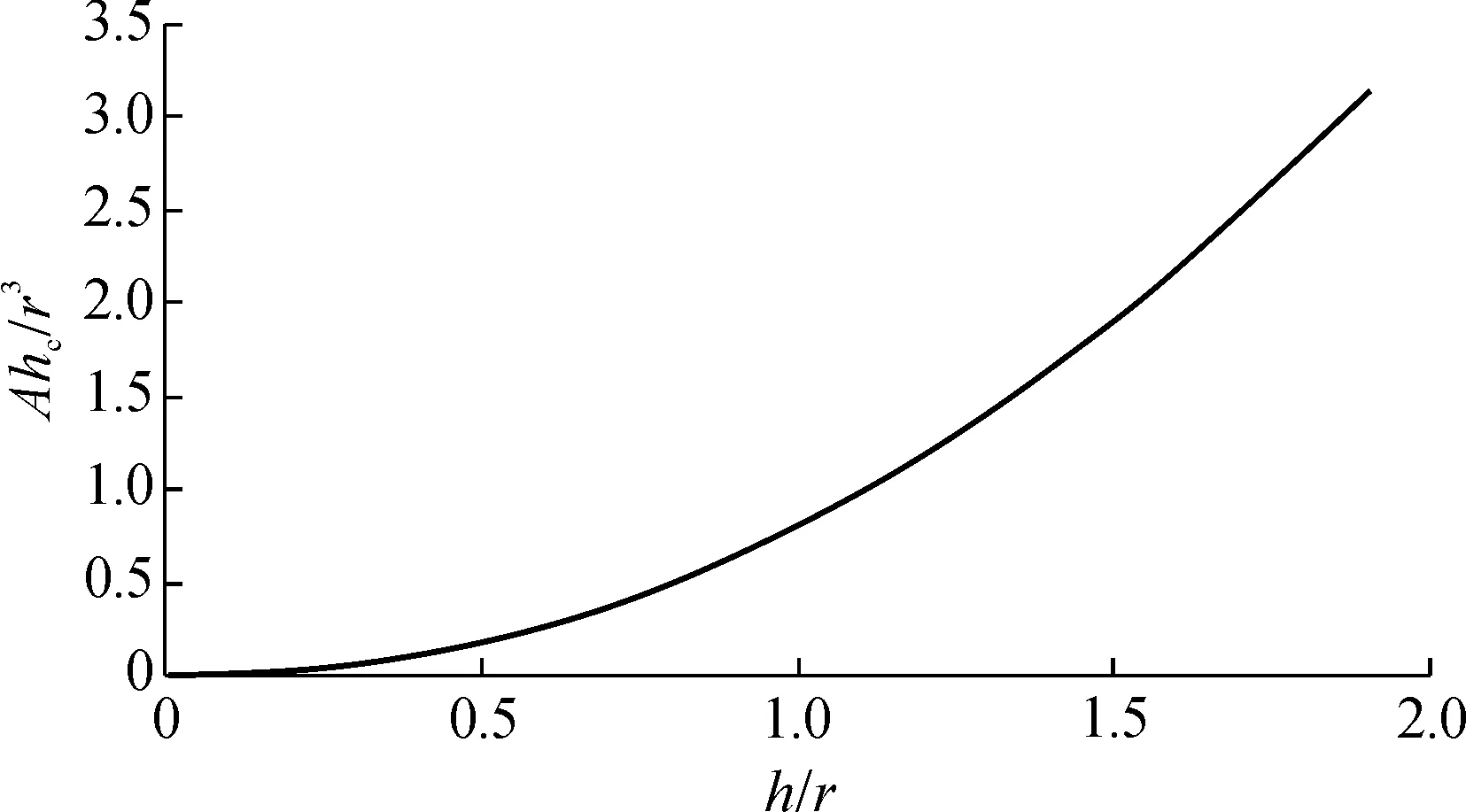
3 断面面积和形心的简化计算


4 算 例
5 结 论
