非线性函数三次型逼近算法研究

宋巨龙，钱富才，梁锦锦

(1.西安石油大学 理学院,陕西 西安 710065；2.西安理工大学 自动化与信息工程学院，陕西 西安 710048)

在非线性控制领域中，二次型最优控制方法是一个值得研究的方向，文献[1] 提出了非齐次双线性二次型最优控制迭代算法、文献[2] 基于二次型性能指标对简单自适应控制系统进行了研究，文献[3] 给出了一个二次型控制方法在风量空调箱优化方面的应用。文献[4] ～[6] 则对广义二次型和类二次型以及矩阵的性质及应用进行了研究，文献[7] 所论及的二次型设计方法则涉及二次型在军事领域的应用，此外二次型还在航空、自动化、化工[7-9]等诸多领域中有着广泛的应用。在最优化方法中，人们也常常将非线性函数展开为二次函数进行近似求解[10]，这里也涉及二次型。受上述文献的启发我们考虑如果能将非线性函数的三阶泰勒多项式加以应用，用三次型替代二次型应该能够得到更为精确的结果。但是目前较为一般的方法是把非线性函数利用其二次函数替代，这是因为多元函数三次以上的泰勒展开式的形式比较复杂，从几何意义上看不很明确，利用起来比较困难。比如文献[11] 对多元函数的泰勒公式进行了研究，但所使用的就是传统的多元函数泰勒展开式，显得较为繁琐而不易理解。此外注意到函数逼近论中很多情况下也是将一个函数用多项式来替代从而达到近似计算的目的[12]，如果我们能给出更高阶的、几何特征正直观的多项式，也会使这种问题得到更精确的结果。

本文根据目前的研究现状，从二次型这一概念及其重要的应用性出发，对二次型进行一个数学意义上的扩展，提出了一个新的概念——三次型。对二次型的运算方式进行稍稍改变，并由此出发给出三次型的定义和运算方法。从向量、矩阵引申出体阵的概念；从二次型扩展到三次型。还将传统的二次型和新提出来的三次型在形式上、运算方式上进行了统一，给出了三次型的各阶导数。

1 二次型

二次型的定义[4]：

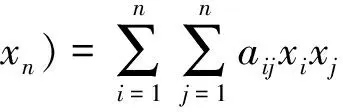
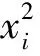
众所周知，二次型由于其形式特殊、性质特殊、应用范围广泛，因而极具研究价值。

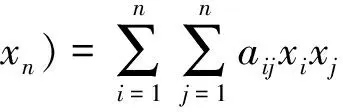
推而广之，不难写出n元k次齐次多项式。

相信很多人也想过这个问题，只不过对其理论意义和应用价值无法确定，另外由于其表现形式已经比较复杂了，失去了二次型通过矩阵运算相对简单的特性，因而如何使其运算简单化，也是需要考虑的一个问题。下面对这些问题逐一进行探讨。

2 三次型的定义

为了使得后面所讨论的问题能够有一个比较简单的形式，先给出一些定义。

定义2称由n个数a1,a2,…,an组成的n维数组为一个1度n维体阵，记为：

即为通常意义上的n维向量，因而1度n维体阵也和向量看作是相同的。

定义3称由n2个数aij(i,j=1,2,…,n)组成的正方形数表为一个2度n维体阵，记为：

其中aij=aji(i≠j,i,j=1,2,…,n)。即通常意义上的n阶方阵。

定义4称由n3个数aijk(i,j,k=1,2,…,n)组成的立方体数阵为一个3度n维体阵，记为：

其中:

aijk=aikj=akji=akij=ajik=ajki

(i≠j, 或j≠k, 或k≠i;i,j,k=1,2,…,n)

定义6设有2度n维体阵:

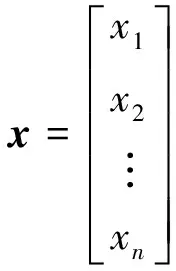
图1 2度n维体阵与x2的乘积法则

如图2所示。

图2 3度n维体阵与x3的乘积法则

3度n维体阵与向量x的幂的乘积方法为：

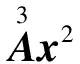
简单地说，分三步进行，每次都是将体阵中的每一列和与该列平行的x1,x2,…,xn作内积，最终形成一个数字。由于体阵的对称性，这种做法可以按可能的任意一种顺序进行，其结果都是一样的。

3 三次型的导数

根据上述定义，从导数的定义出发，不难推出以下关于三次型的各阶导数的结论。

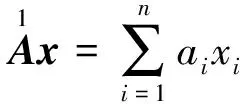
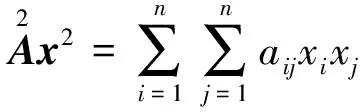
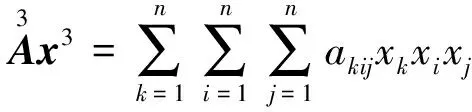
对于上面的结论，因为都非常简单，所以这里只对3)中的ⓒ进行证明。

证明：由于函数的表达式是由n3个项的和构成的，所以我们只需证明任意一项的三阶导数都等于其系数即可。设任意一项为akijxkxixj, 分3种情形讨论。

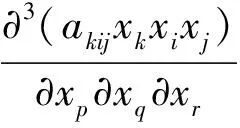
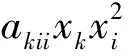
综合以上，可知命题3)的ⓒ是成立的。

当我们给出上述表示方法，并且有了相应函数的导数记法，原来已有的多元函数的一些表示方法可以写成和人们熟悉的一元函数一样。

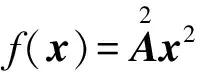
例3 此外还可以定义三次多项式函数：

其一阶导数为：

二阶导数为:

三阶导数为:

例4 三阶偏导数连续的多元函数的泰勒公式可以写为：

f(x)=f(x0)+f(x0)(x-x0)+

4 结 论

提出了体阵的概念，并通过体阵的定义推导出体阵的导数的形式和导数，给出了一些数学结果及其记法，给出了几个体阵的运算方法，使得复杂问题得以简化规范，并且将多元函数的符号记法及运算结果与一元函数的符号记法及运算结果进行了统一，使得多元函数的表示更加简洁、更易于理解，该结果有一定的实用价值。

另外，当笔者给出三次型之后，很可能有类似于二次型的应用结果。例如是否存在三次型的特征值和特征向量，其意义如何？再如，动态系统的稳定性一直是理论界和工程界关注的热点问题之一，因为不稳定的系统无法付诸实际应用，而Lyapunov方法是解决这类问题的有力工具。

对于线性系统，判断平衡点稳定性的基本思想为：首先构造一个具有二次型的Lyapunov函数，然后求解Lyapunov方程，就可给出所需的结果。

对于多元多项式非线性系统，用类似的思想也可以对平衡点的稳定性进行判断，只不过需要把二次型的Lyapunov函数推广到三次正定型，这方面的潜在应用还有待于进一步研究。

参考文献：

[1] 李俊民，邢科义，万百五.连续时间非齐次双线性二次型最优控制迭代算法[J].西安电子科技大学学报，2000，27(5):630-634.

Li Junmin, Xing Keyi, Wan Baiwu. An iterative algorithm of optimal control for the non-homogenous bilinear quadratic problem[J]. Journal of Xidian University,2000,27(5):630-634.

[2] 尹怡欣，孙一康，舒迪前.具有二次型性能指标的简单自适应控制算法及其应用[J].控制与决策，2000，15(2):236-238.

Yin Yixin, Sun Yikang , Shu Diqian. Simple adaptive control algorithm with quadratic performance and its application[J]. Control and Decision, 2000,15(2)：236-238.

[3] 王军,王雁,王瑞祥,等.采用逆系统设计和二次型最优控制提高变风量箱的性能[J].上海交通大学学报，2006，40(8):1431-1436.

Wang Jun, Wang Yan, Wang Ruixiang,et al.The performance improvement of variable air volume box through inverse system design and quadratic optimal control[J].Journal of Shanghai Jiaotong University,2006,40(8)：1431-1436.

[4] 刘丁, 赵豆, 杨延西.基于快速立体匹配的基本矩阵估计方法[J].西安理工大学学报，2009，25(1):1-7.

Liu Ding, Zhao Dou, Yang Yanxi. Fundamental matrix estimation method based on fast stereo matching[J].Journal of Xi’an University of Technology, 2009,25(1):1-7.

[5] 陈雪波，徐望宝，李小华,等.非线性系统零解稳定性判定的广义二次型方法[J].控制与决策，2007，22(1)：81-84.

Chen Xuebo, Xu Wangbao, Li Xiaohua,et al.General ized quadratic form method for zero2 solution stability of nonlinear systems[J].Control and Decision,2007，22(1)：81-84.

[6] 刘忠汉, 吴宏鑫.类二次型最优控制方法在自主对接控制中的应用研究[J].宇航学报，2002，32(2)：44-49.

Liu Zhonghan, Wu Hongxin. Application of a similar quadratic ptimization control method in the autonomous docking control[J].Journal of Astronautics, 2002, 32(2)：44-49.

[7] 陈浩，华灯鑫，张毅坤,等.一种基于变换矩阵的激光雷达数据无量纲统一化转换方法[J].西安理工大学学报，2014，30(1)：1-7.

Chen Hao,Hua Dengxin,Zhang Yikun, et al. A conversion method for radar data non-dimensionalization and standardization based on transform matrix [J]. Journal o f Xi’an University of Technology, 2014 30(1):1-7.

[8] 邵克勇，蒋锐，李文成,等.基于二次型性能指标的不确定混沌系统最优控制器设计[J].化工自动化及仪表，2013，40(11)：1347-1350.

Shao Keyong，Jiang Rui，Li Wencheng,et al. Design of optimal controller for uncertain chaotic systems based on quadratic performance index[J].Control and Instruments In Chemical Industry, 2013：40(11), 1347-1350.

[9] 王双进，冯磊,黄贤军,等.用二次型的正定性判断晶体相稳定性[J].河北工业大学学报，2007，36(1)：30-34.

Wang Shangjin，Feng Lei，Huang Xianjun，et al.The judgement for crystal stability of phase in positive definite quadratic form[J].Journal of Hebei University of Technology, 2007, 36(1)：30-34.

[10] 宋巨龙，王香柯，冯晓慧.最优化方法[M].西安:西安电子科技大学出版社，2012.

[11] 秦国强.多元函数的泰勒公式及其应用[J].吕梁教育学院学报，2013，30(2)：103-105.

Qin Guoqiang.Taylor rule of multivariate functions with it's application[J].Journal of Lvliang Education Institute,2013,30(2):103-105.

[12] 莫国瑞，刘开第. 函数逼近论方法[M].北京:科学出版社，2003.