基于Contourlet变换的多聚焦图像融合算法研究

李白萍， 孙启昌， 张雪燕

(1.西安科技大学 通信与信息工程学院， 陕西 西安 710054；2.成都航空职业技术学院 计算机工程系， 四川 成都 610100)

0 引 言

图像融合技术是以图像为主的数据融合，是把不同传感器获得的同一场景的多幅图像或同一传感器获得同一场景的多幅图像采用一定的方法合并成一幅图像的过程。图像融合技术作为信息融合的组成部分，已被应用于多聚焦图像的处理和分析。

目前，多聚焦图像融合常用的方法有平均加权算法[1]、PCA变换法[2]、HIS变换法[3]和小波变换等方法。线性平均加权法的图像融合信噪比低灰度差异很大，图像融合效果较差。PCA变换与HIS变换造成图像中频谱信息的损失。小波变换被广泛应用，具有良好的空间(时间)和频率的局部化分析，它通过伸缩和平移运算对信号逐步进行多尺度细化，因而可有效地从信号中提取信息，可聚集到信号的任意细节[4-5]。但是小波变换在高维情况下，不能充分捕捉图像轮廓和线状等信息，因此，必须寻找比小波变换更优越的一种方法。2002年Do和Veterli提出一种新的图像二维表示方法：Contourlet变换[6-8]。

Contourlet变换具有方向性、局域化、多尺度和多分辨率等优点[9]，本文将Contourlet变换应用于图像融合，提出一种基于Contourlet变换的多聚焦图像融合算法。

1 Contourlet变换原理

Contourlet变换的基本思想是首先由拉普拉斯金字塔(Laplacian pyramid，LP)[10]变换对输入的信号进行多尺度分解以捕获奇异点，接着利用方向滤波器组(Directional filter bank，DFB)[11]进行方向分解，对方向信息位置相近的奇异点汇集成轮廓段的方法来逼近原信号。

选用Burr和Adelson于1983年提出的拉普拉斯塔式滤波器结构(LP)[12]对信号多尺度分解来捕捉奇异点。LP分解产生一个分辨率为原始信号一半的低频子带和原始信号分辨率相同的高频子带，高频子带是通过采样滤波后的原始信号减去低频子带的差值信号，对于低频子带逐步进行LP变化分解，得到一系列的低频子带和高频子带。二维方向滤波器组(DFB)按方向分解信号并具有很好的重构性，对于LP分解得到的每一级高频分量上，进行方向性分析，在任意尺度上可将频域分解得到2的n次方个方向子带，信号每次经LP子带分解产生的高通子带信号输入DFB，逐步将奇异点连成线形结构，从而捕获信号中的轮廓。DFB充分表现了高频部分，LP分解将信号分解成高频部分与低频部分，Contourlet变换充分利用了两者的共同特点。

2 Contourlet变换的多聚焦图像融合算法

由Contourlet变换的原理可知，对于任意图像，近似和平均信息属于低频部分，边缘和纹理等细节信息属于高频部分。因此，本文提出了基于Contourlet变换的多聚焦图像融合算法，该算法是利用Contourlet变换将图像的低频子带与高频子带进行分离，低频部分采用平均方法求出相关系数，高频部分采用绝对值取大的方法求出相关系数，对两个相关系数进行融合处理，生成Contourlet融合系数，最后再进行Contourlet反变换得到融合后的图像。Contourlet变换的图像融合流程如图1所示。

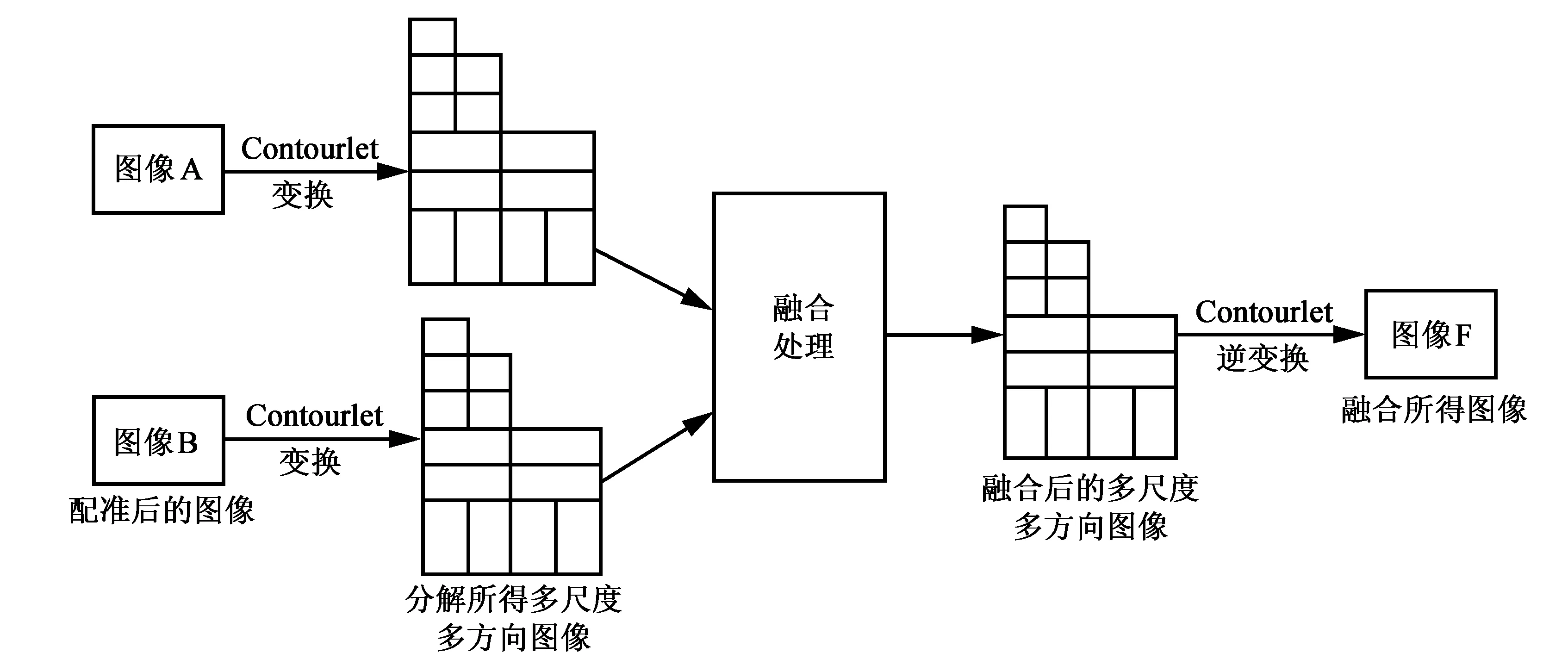
图1 Contourlet变换的图像融合流程图

设A、B为两幅多聚焦图像，F为融合后的图像。其融合处理的基本步骤如下：

(1)对A、B两幅多聚焦图像进行几何配准。

(2)对A、B两幅多聚焦图像分别进行多级多方向Contourlet变换，对于最终得到的变换系数XA，XB，设融合图像的变换系数为ZF。则按照以下规则进行融合处理：

①对低频系数，用平均方法求出相关系数

(1)

②对高频系数，直接采用绝对值取大的方法求出相关系数

ZF(n)=max(XA(n),XB(n))，

(2)

最终得到融合图像对应的Contourlet分解系数ZF。

(3)对融合后的Contourlet系数ZF进行Contourlet反变换，所得重构图像即为融合图像。

3 融合结果及分析

3.1 图像融合结果

使用MATLAB软件进行仿真，选取512×512的图像，图像融合结果如图2所示。其中图2(a)右边目标较为清楚，图2(b)左边的目标较为清晰，图2(c)—(e)为两幅多聚焦图经过平均加权算法、小波变换算法和本文算法所得的融合图像。

(a)右边目标较为清楚 (b)左边的目标较为清晰

(c)平均加权算法 (d)小波变换算法 (e)本文算法 图2 图像融合结果

从视觉效果上来看，本文提出的融合方法的结果(图2(e))保留了图2(a)和图2(b)的绝大部分信息，在图像细节信息上具有明显的改善，融合后的图像在边缘轮廓的细节方面更为清晰。

3.2 定量分析

从图像处理的角度，采用平均梯度、平均灰度及熵指标可以对图像融合进行客观的定量分析：(1)平均梯度可以更好地反映图像对微小细节反差表达的能力，平均梯度越大，图像越清晰；(2)平均灰度是人眼观察图像的亮度，其值范围在128附近，则人眼观察效果较好；(3)熵是图像融合后重要的信息，值越大，表明融合后的图像信息越丰富，图像融合效果越好。分析结果见表1。

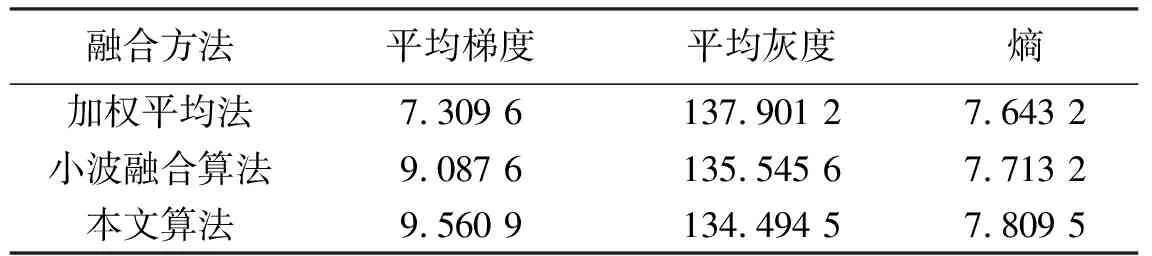
表1 融合效果指标

通过对融合后的图像采用平均梯度、平均灰度及熵计算可知，基于Contourlet变换的图像融合结果在平均梯度、平均灰度及熵指标上均优于小波变换和加权平均。图像融合细节效果较好，达到预期效果。

4 结 论

本文利用Contourlet变换将图像的低频子带与高频子带进行分离，低频部分采用平均方法求出相关系数，高频部分采用绝对值取大的方法求出相关系数，对两个相关系数进行融合处理，得到的图像在边缘轮廓细节上更为清晰。与小波变换、加权平均的图像融合进行试验比较，采用平均梯度、平均灰度及熵等指标对融合效果进行分析，验证了本文提出的基于Contourlet变换的多聚焦图像算法具有较好的融合效果。

[参考文献]

[1] 冼广铭,王知衍,黄鲲.紧支撑二维小波多尺度融合图像效果评价[J].计算机工程与设计,2006,27(15)：2740-2743.

[2] 贾永红.多源遥感影像数据融合方法及其应用的研究[D].武汉：武汉大学,2001.

[3] 焦李成,谭山.图像的多尺度几何分析：回顾和展望[J].电子学报,2003,31(12A)：1975-1981.

[4] LI H,MANJUNATH B S. Multisensor image fusion using the wavelet transform[J].Graphical Models and Image Process,1995,57(3)：235-245.

[5] 刘斌,彭嘉雄.基于小波包变换的区域图像融合方法[J].计算机工程与应用,2004,21(5)：36-40.

[6] Do M N,VETTERLI M.Contourlets[C]//STOECKLER J,WELLAND G V.Beyond Wavelets.New York：Academic Press,2002.

[7] Do M N,VETTERLI M. The contourlet transform：an efficient directional multiresolution image representation[J].Image Processing,2005,14(12)：2091-2106.

[8] 李存军,刘良云,王纪华,等.两种高保真遥感影像融合方法比较[J].中国图象图形学报,2004,9(11)：1376-1385.

[9] Do M N.Directional Multiresolution Image Representations[D].Lausanne：Swiss Federal institute of Technology Lausanne,2001.

[10] 敬忠良,肖刚,李振华.图像融合——理论与应用[M].北京：高等教育出版社,2007：52-53.

[11] BAMBERGER R H,SMITH M J.A filter bank for the directional Decomposition of images：theory and design[J].IEEE Transactions on Signal Procesing,1992,40(4)：882-893.

[12] 张强,郭宝龙.应用第二代Curvelet变换的遥感图像融合[J].光学精密工程,2007,15(7)：1130-1136.