基于人工智能的人民币/美元汇率组合预测模型

张延利

(泸州职业技术学院 基础部， 四川 泸州 646005)

0 引 言

人民币汇率制度改革在坚持“主动性、可控性和渐进性”三原则[1]的前提下，实行直接标价法，即100美元折合多少人民币，以此来衡量升值和贬值。从1994年1月1日到2013年3月6日，人民币/美元汇率从870.00到627.45，下降了27.88%。特别是自2003年以来面临美国、欧盟、日本等发达国家的不断施压及国际舆论，人民币不断升值。

我国的经济增长是贸易依赖性增长，人民币升值会使得商品成本加大、价格升高，导致出口产品竞争力降低，企业经济不景气；人民币升值会导致海外资金投资减少，国内经济增长的动力降低，国际流动资金投机机会加大，我国金融危机风险加大；此外，人民币升值使得进口商品价格放低、物价降低，给中国的通货紧缩带来更大的压力。所以，对人民币/美元汇率进行预测显得尤为重要。

1 数据特性分析

1.1 数据选取和特性

汇率收益率序列具有以下3个特征[2]：

(1)尖峰厚尾。受外汇市场汇率频繁出现价格变化较大且变化突然的影响，汇率时序数据(按时间先后形成的汇率数据)往往出现均值点峰值较高和厚尾的特性。

(2)波动性聚集。即在汇率收益较大的时间点后往往出现大收益，汇率收益较小的时间点后往往出现小收益。

(3)杠杆效应。是指波动率对市场下跌的反应比对市场上升的反应更加迅速等特征。

在国家外汇管理局网站(http：//www.safe.gov.cn/model_safe/index.html)，选取自2012年4月18日到2013年3月6日(仅限工作日)共213个人民币/美元汇率数据用于构建单模型，将2013年3月7日到4月3日的20个汇率数据用于模型预测效果评定。

1.2 GARCH类模型选择

针对人民币/美元汇率的上述特性，利用单模型预测时，采用ARMA模型和能刻画异方差特性的GARCH(1,1)类模型。因ARMA模型、GARCH(1,1)类模型只能对平稳时间序列进行建模，所以先对汇率{xt}进行对数差分，得到的差分序列即为收益率序列：yt=100(lnxt-lnxt-1)。这里xt为每日的即期汇率，xt-1为前一天的汇率，yt为对数收益率。利用Eviews 5.0建立ARMA模型：

yt=0.158 249 379 2yt-1-0.202 912 883 3εt-5+εt，t=1，2，…

(1)

对建立的ARMA模型拟合后的残差序列进行异方差性检验，结果见图1。

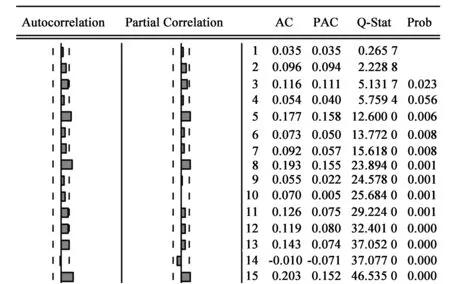
图1 残差平方检验

图1最右边的概率P值除第二个外均小于0.05，说明残差平方序列是序列相关的，残差序列具有异方差性。

为考察信息冲击曲线是否具有非对称性，再建立EGARCH(1,1)模型(结果见表1)：

ln(GARCH)=C(3)+C(4)×ABS(RESID(-1))/@SQRT(GARCH(-1))+

C(5)×RESID(-1)@SQRT(GARCH(-1))+C(6)×ln(GARCH(-1))。

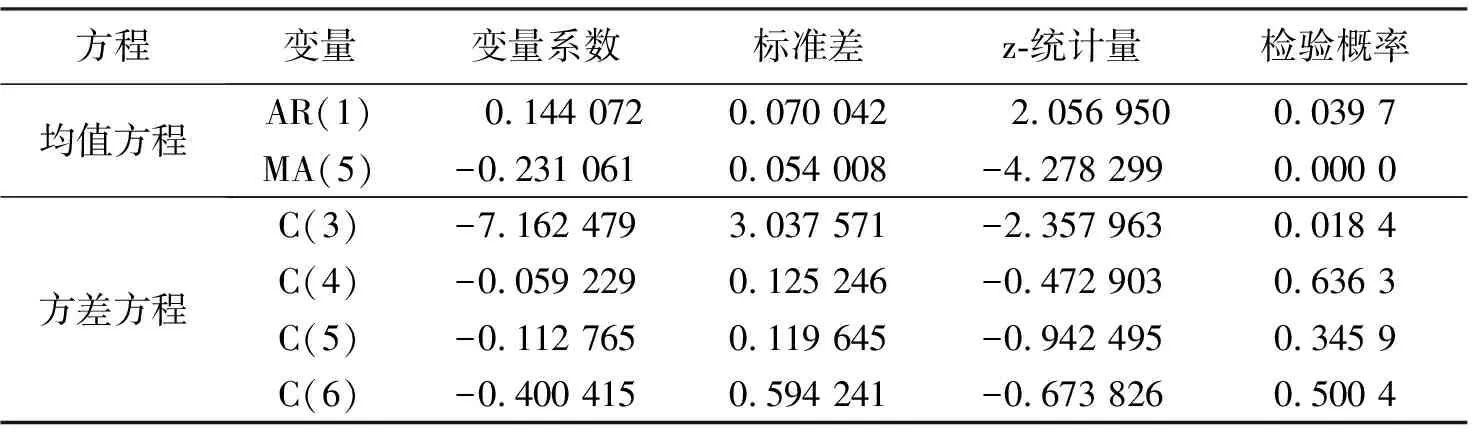
(2)

表1中C(5)的概率P值大于显著性水平α=0.05，说明C(5)是不显著的，即收益率时间序列不存在非对称效应，应当建立GARCH(1,1)模型：

(3)

其中，GARCH(-1)为前一期的预测方差，RESID(-1)2为前一期残差的平方。

2 建立组合预测模型

2.1 协整关系分析

基于人民币/美元汇率时序数据一般具有非平稳性，所以首先利用单位根检验方法中的ADF检验，分别检验原数据序列及利用ARMA模型、GARCH(1,1)模型得到的拟合值序列的平稳性。若两个拟合值序列的平稳性与原数据的平稳性一致，则选择的预测模型合适。否则，选择的模型不恰当，应修改模型或更换预测模型。

其次，当检验原数据序列及利用ARMA模型、GARCH(1,1)模型得到的拟合值序列的平稳性一致时，则进行协整检验。分别将ARMA模型、GARCH(1,1)模型得到的拟合值与被预测时序值做线性回归(拟合值做自变量，被预测值做因变量)，得到回归模型相应的残差序列[3]，记为f1和f2。

最后，利用ADF检验方法检验残差序列f1和f2的平稳性。若f1和f2均平稳，说明ARMA模型、GARCH(1,1)模型得到的拟合值序列和原数据序列存在可以建立线性模型的协整关系[4]，此时建立线性组合模型是合适的。若f1和f2中至少有一个是非平稳的，说明ARMA模型、GARCH(1,1)模型得到的拟合值序列和原数据序列的协整关系不存在，建立线性组合模型是不合适的，应考虑其它组合方法。

2.2 协整检验结果

利用协整检验，ARMA模型、GARCH(1,1)模型得到的拟合值序列与原数据序列不具有协整关系。为与单模型进行比较，利用最优加权方法建立线性组合预测模型：

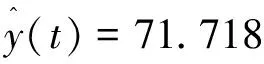
9×GARCH(t)-70.718 9×ARMA(t)，t=214,215,…,233。

(4)

2.3 基于人工智能的非线性组合预测

2.3.1 人工智能神经网络简介

人工智能神经网络是由大量的处理单元组成的非线性大规模自适应动力系统，是在现代生物神经生理科学研究成果的基础上提出来的，是人们试图通过模拟大脑神经网络处理、记忆信息的方式，设计的一种使之具有人脑那样的信息处理能力的新“机器”。它将多个信息处理单元通过某种方式进行连接，形成计算系统，该系统对外来信息进行处理，利用处理后的数据模拟人的神经网络，建立信息处理模型，实现仿照人脑处理信息的功能。

2.3.2 BP神经网络算法流程图

BP神经网络是一种误差反向传播及权值不断调整的神经网络，具有联想、记忆、较强的容错能力、良好的非线性映射能力及良好的泛化能力[5]，能根据输入、输出数据特点归纳数理规律，进而以任意精度拟合非线性函数，如图2所示。

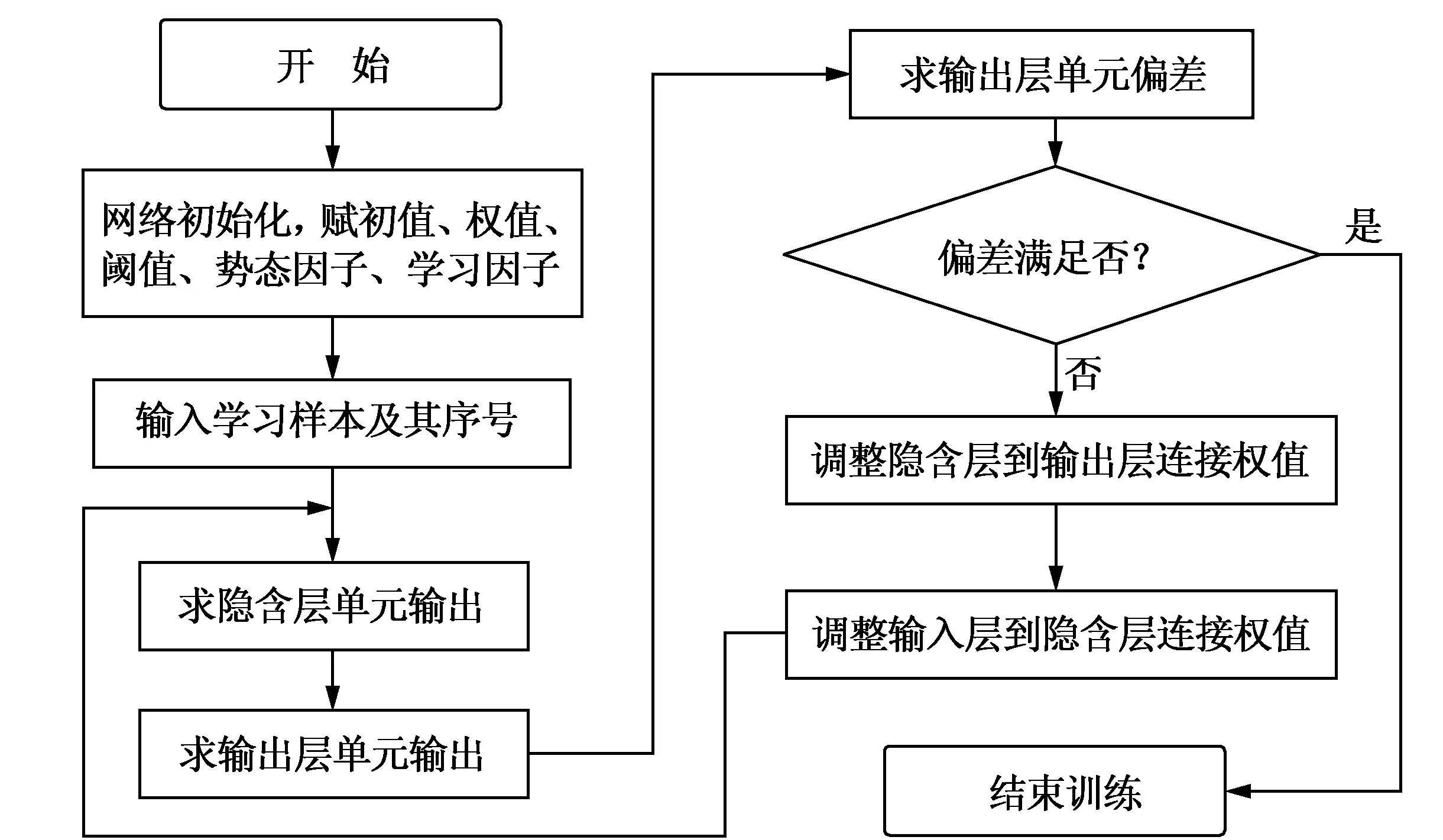
图2 BP神经网络算法流程图

2.3.3 基于BP神经网络的非线性组合模型

因ARMA模型、GARCH(1,1)模型与原数据序列无协整关系，且线性组合精度不高，考虑采用非线性组合方式进行预测。在非线性组合模型建立中利用单隐层BP神经网络对预测模型进行非线性组合。单隐层BP神经网络构建和调用：

net=newff([-11，-11]，[10，1]，{“tansig”，“pureline”}，“trainbr”，“learngdm”，“msereg”)。

如图3所示为三层BP神经网络示意图。图中的IW{1,1}为输入层连接权向量[5]，b{1}为输入接点阈值向量，LW{2,1}为输出层的连接权向量，b{2}为输出层阈值向量。得到的预测结果见表2。

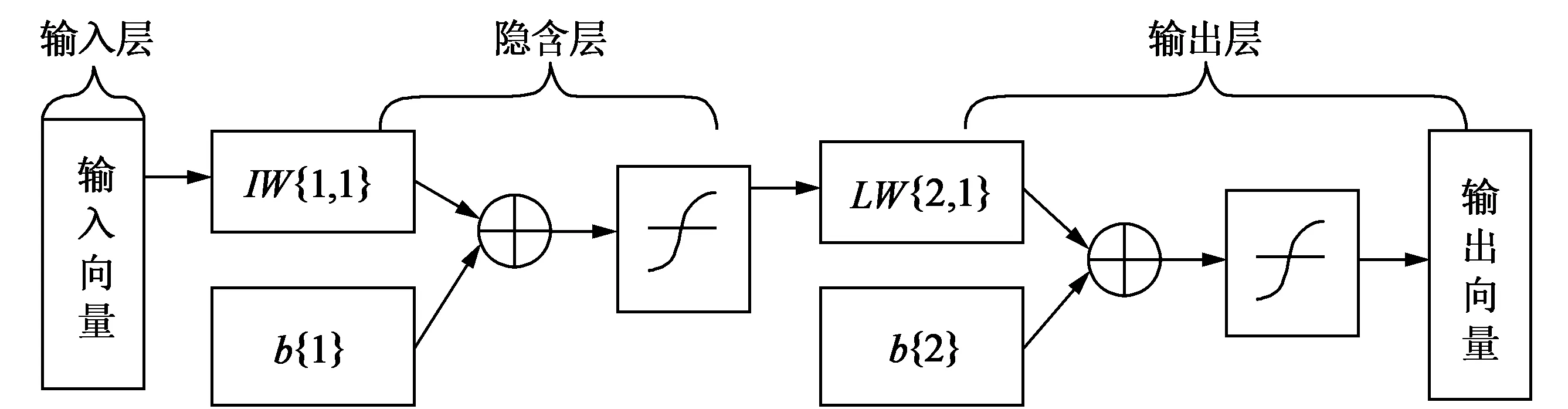
图3 三层BP神经网络

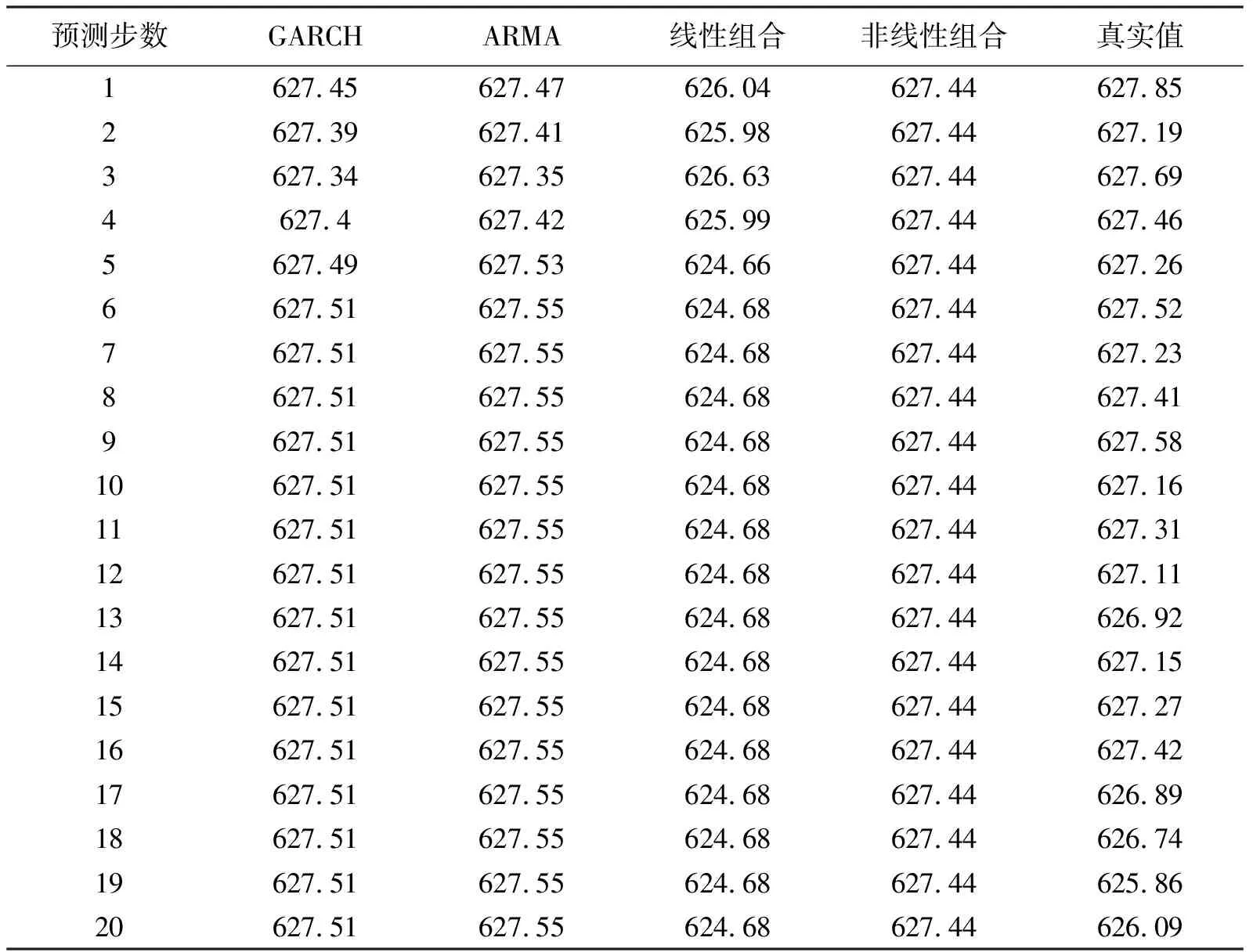
预测步数GARCHARMA线性组合非线性组合真实值1627.45627.47626.04627.44627.852627.39627.41625.98627.44627.193627.34627.35626.63627.44627.694627.4627.42625.99627.44627.465627.49627.53624.66627.44627.266627.51627.55624.68627.44627.527627.51627.55624.68627.44627.238627.51627.55624.68627.44627.419627.51627.55624.68627.44627.5810627.51627.55624.68627.44627.1611627.51627.55624.68627.44627.3112627.51627.55624.68627.44627.1113627.51627.55624.68627.44626.9214627.51627.55624.68627.44627.1515627.51627.55624.68627.44627.2716627.51627.55624.68627.44627.4217627.51627.55624.68627.44626.8918627.51627.55624.68627.44626.7419627.51627.55624.68627.44625.8620627.51627.55624.68627.44626.09

2.4 预测结果分析

表3 预测效果评价

3 结 论

(1)汇率时序数据具有异方差性，所以GARCH(1,1)模型预测效果优于ARMA模型。

(2)在利用多个模型进行组合预测时，应首先对各模型与被预测序列的线性关系(协整关系)存在性进行检验。若各模型均与被预测序列具有线性关系，则可建立线性组合模型；反之，应采用非线性组合模型预测效果较好。

[参考文献]

[1] 黄勤.浅析人民币升值的原因[J].消费导刊,2006(12):64.

[2] 池启水,刘晓雪.人民币汇率波动特征实证研究[J].统计与决策,2007(23):120-122.

[3] 张延利,张德生,刘常明,等.基于BP神经网络的黄金价格非线性组合预测模型[J].黄金,2011,32(9):5-8.

[4] 张延利.基于协整理论的人民币/美元汇率组合预测模型[J].陕西理工学院学报:自然科学版,2012,28(5):60-63.

[5] 张延利.基于BP神经网络的黄金价格非线性预测[J].黄金,2013,34(7):8-10.

[6] 魏巍贤.非平稳时间序列的组合预测建模条件及应用[J].系统工程与电子技术,1998,10(6):30-33.

[7] 范剑青,姚琦伟.非线性时间序列[M].北京:高等教育出版社,2005.

[8] 董长虹.神经网络与应用[M].北京:国防工业出版社,2005.