基于自适应双正则化支持向量机的群体基因选择

陈留院， 穆晓霞， 李钧涛

(1．河南师范大学学报编辑部 河南新乡453007;2．武汉理工大学信息工程学院 湖北武汉430070;

3．河南师范大学计算机与信息工程学院 河南新乡453007;

4．河南师范大学数学与信息科学学院 河南新乡453007)

0 引言

以支持向量机为核心内容的统计学习理论是由Vapnik等人在20世纪90年代提出的，目前仍处在不断发展阶段［1－4］．支持向量机一经提出，就被成功地应用于微阵列基因表达数据的分类与基因选择中［5］．由于癌症、艾滋病等复杂疾病是由一些基因的共同作用引起的，所以群体基因选择在最近几年引起了广泛关注［2－4，6］．文献［2］通过结合弹性网络惩罚与平方误差损失函数，提出了在分类的同时能成群选择相关基因的弹性网络模型．文献［3］通过结合弹性网络惩罚与huberized损失函数提出了混杂huberized的支持向量机．文献［4］通过结合弹性网络惩罚与hinge损失函数提出了双正则化支持向量机．上述弹性网络惩罚方法虽然均能成群地选择基因，但却无法消除被选择的基因群内存在的冗余基因．为了解决该问题，Li等人通过引入数据驱动权重到惩罚项，提出了改进的弹性网络模型［7］和部分自适应弹性网络模型［8］，但上述两种方法均是回归方法．

受文献［7－9］中数据驱动思想的启发，本文通过结合自适应弹性网络惩罚和性能优越的hinge损失函数，构建自适应双正则化支持向量机并证明了其具有自适应群体基因选择性能．

1 问题描述

给定一个具有p个基因表达水平的n个微阵列训练样本(x1，y1)，(x2，y2)，…，(xn，yn)，其中xi=(xi1，xi2，…，xip)是样本输入，yi∈{+1，－1}是样本标签，学习问题是寻找一个决策函数f:Rp→{+1，－1}来预测新样 本的 标签．令 Y=(y1，y2，…，yn)T，X=(x1;x2;…;xn)=(x(1)，x(2)，…，x(n))，其 中 x(j)=(x1j，x2j，…，xnj)T被称为预测子．根据正则化理论框架，支持向量机可表示为如下的损失+惩罚形式，

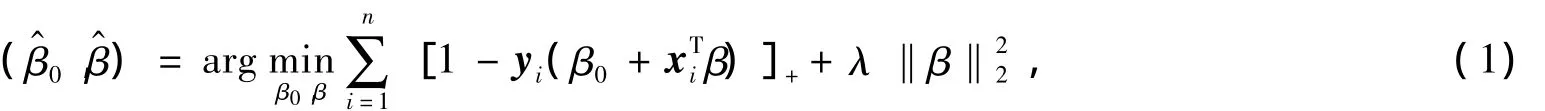
其中，［*］+表示hinge损失函数，λ＞0是正则化参数，相当于调谐参数C，对于输入向量x，分类规则由(sgn(f(x))=sgn+xT))给出．需要指出的是，支持向量机的优越性能不仅体现在(1)式中的2－范数惩罚项，其分类性能的优越性很大程度上依赖于所采用的hinge损失函数．正如Hastie等人所证明的那样，hinge损失函数的优越性能，确保了支持向量机分类器满足Bayesian分类准则，进而展现出良好的分类性能［10］．基于上述考虑，通过结合hinge损失函数与弹性网络惩罚，Wang等人［4］提出双正则化支持向量机，

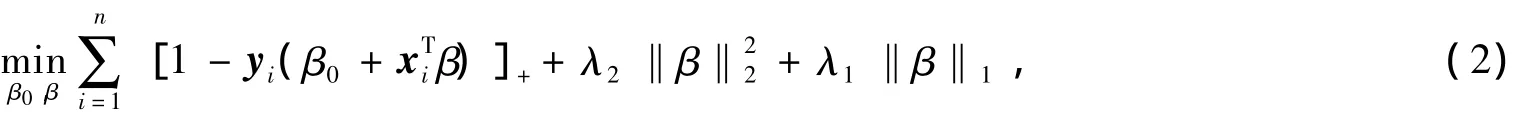
其中λ1，λ2≥0是正则化参数．双正则化支持向量机采用的弹性网络惩罚是1－范数惩罚和2－范数惩罚的一个线性组合，从而使其既具有1－范数惩罚学习机的自动变量选择性能，还具有群体变量选择的性能．和其他弹性网络惩罚方法一样，双正则化支持向量机虽然能成群地选择基因，但却无法消除被选择的基因群内存在的冗余基因．

2 自适应双正则化支持向量机

给定一个训练样本集{(xi，yi)}ni=1和参数 α0(一般地，令 α0≤0．05)，类似于文献［8］，令)表示给定参数α=α0时弹性网络的解，其分量(α0)的大小表示基因j对分类器的贡献．不失一般性，假设有如下排列顺序:．令mδ为数据集的最大下标max通过采用加权惩罚的方法，文献［8］提出部分自适应弹性网络惩罚，

其中，

本文将部分自适应弹性网络惩罚(3)引入到hinge损失函数中，提出自适应双正则化支持向量机，

其中 φ(yi，f(xi))表示 hinge损失函数，f(xi)=β0+xTiβ．由(4)式解出的)来构造决策函数 f(x)=+xT，进而可由其符号函数来判别新样本的标签，即 sgn(f(x))=sgn+x)为其分类器．

与双正则化支持向量机［4］相比，所提自适应双正则化支持向量机由于把数据驱动权重引入到惩罚函数里，进而能取得更好的基因选择性能．与部分自适应弹性网络［8］相比，自适应双正则化支持向量机采用了性能优越的hinge损失函数，更适用于处理分类问题．此外，由于hinge损失函数φ(t)是Lipschitz连续的，所以存在Lipschitz常数M＞0，使得(5)式成立，

接下来将证明自适应双正则化支持向量机能自适应地成群选择基因，即激励一种自适应群体基因选择效应．

定理1 给定数据集(Y，X)和正则化参数(λ1，λ2)，假设是自适应双正则化支持向量机(4)的解，那么，对任意的 j，l≤mδ有不等式(6)成立，

如果输入变量x(j)，x(l)是零均值和标准化的，那么有

其中

利用(5)式可得

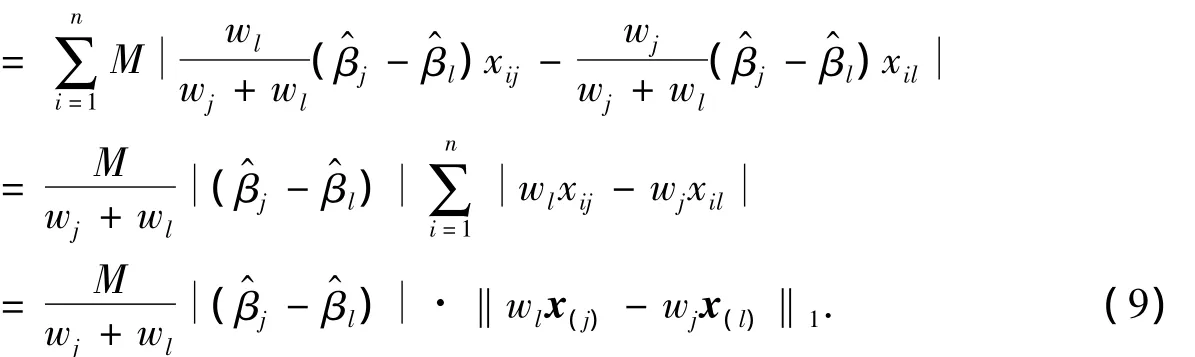
由W的构造，可得

当 l，j≤mδ时，

考虑到

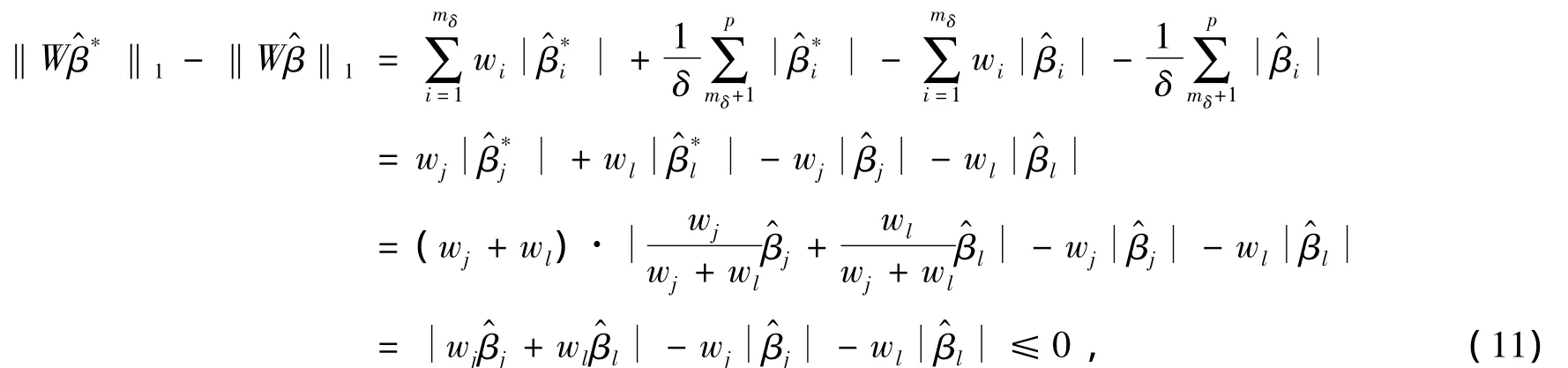
将(9)、(10)、(11)式带入到(8)式可得

移项整理后可得

如果x(j)，x(l)是零均值和标准化的，则

进而有

定理证毕．

应该指出，对于j≥m和l≤m的情况，定理1仍然成立，唯一不同的地方是用δ代替(α0)．当j，l≥m

δδδ时，由W的构造可知道也发生了变化，即

类似于定理1的过程可得

如果输入变量x(j)，x(l)是零均值和标准化的，那么有

3 结束语

考虑到hinge损失函数的优良分类性能和部分自适应弹性网络优良的基因选择性能，本文提出了自适应双正则化支持向量机模型，从理论上证明了其具有自适应群体基因选择性能，并给出了具体的数学表达形式．

［1］ 王红蔚，席红旗，孔波．一种新的半监督支持向量机［J］．郑州大学学报:理学版，2012，44(3):66－68．

［2］ Zou H，Hastie T．Regularization and variable selection via the elastic net［J］．J Royal Statistical Society B，2005，67(2):301－320．

［3］ Wang L，Zhu J，Zou H．Hybrid huberized support vector machines for microarray classification and gene selection［J］．Bioinformatics，2008，24(3):412–419．

［4］ Wang L，Zhu J，Zou H．The doubly regularizrd support vector machine［J］．Statistica Sinica，2006，16(2):589 －615．

［5］ Guyon I，Weston J，Barnhill S，et al．Gene selection for cancer classification using support vector machines ［J］．Machine Learning，2002，46(1):389 －422．

［6］ 王小玉，李钧涛，陈留院．稀疏对数回归及其在基因选择中的应用［J］．河南师范大学学报:自然科学版，2012，40(5):153–156．

［7］ Li J，Jia Y．An improved elastic net for cancer classification and gene selection［J］．Acta Automatica Sinica，2010，36(7):976－981．

［8］ Li J，Jia Y，Zhao Z．Partly adaptive elastic net and its application to microarray classfication［J］．Neural Comput and Applic，2013，22(6):1193 －1200．

［9］ 高建来，运士伟，张永胜．融合粗糙集与球形支持向量机的多分类识别［J］．河南科技大学学报:自然科学版，2011，32(5):77－80．

［10］ Hastie T，Rosset S，Tibshirani R，et al．The entire regularization path for the support vector machine［J］．Journal of Machine Learning Research，2004，5:1391 －1415．