一个带自相容源的变系数(3+1)维KP方程

温丹华， 赵晓焱

(1.郑州师范学院 河南郑州450044;2.河南师范大学计算机与信息工程学院 河南新乡453007)

0 引言

有效求出孤立子方程的精确解并研究其解的性质一直是非常重要而又基本的课题.随着孤立子理论的不断发展，如何构造带自相容源的孤立子方程并对其求解变得非常重要，由胡星标和王红艳提出的源生成法［1-3］是解决此类问题的有效方法.

本文用源生成法来构造和求解带自相容源的变系数(3+1)维KP方程，并给出其一组贝壳隆变换［4］，考虑变系数(3+1)维 KP方程［5］?通过对数变换，方程(1)可以化为双线性形式，

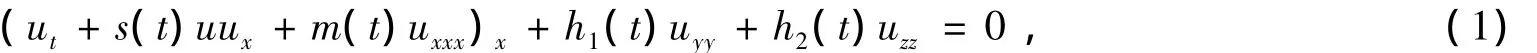
其中D是Hirota双线性算子，并且方程(2)有Gramm型行列式解［5－6］，

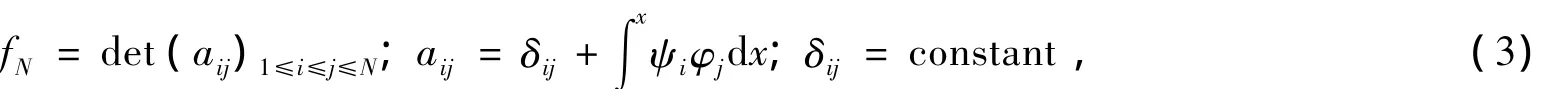
其中函数φi，ψi满足微分方程:

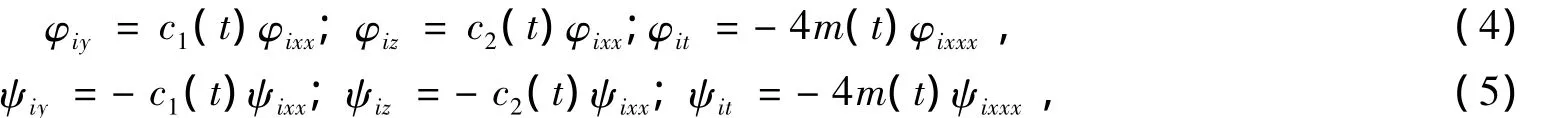
1 带自相容源的变系数(3+1)维KP方程

根据源生成法的步骤，首先对(3)式的函数f作改变，

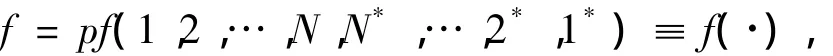
其中pfaff式的元素定义为:

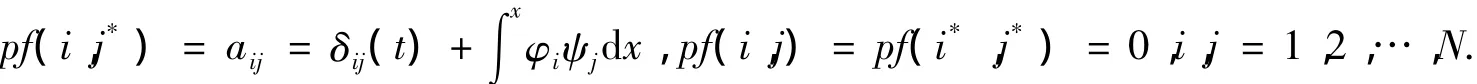
此时，还需要引进一些新的函数Gj(t)和Hj(t)，其定义为:

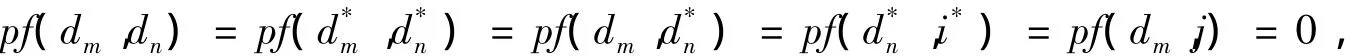
定理1 式(6)～(8)所定义的函数f，Gj，Hj满足双线性方程:

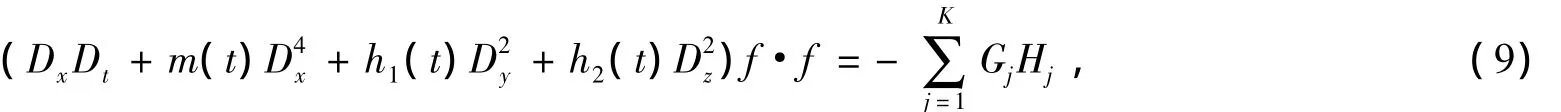
证明 利用pfaff式技巧和式(4)、(5)，通过计算得f的微分公式:

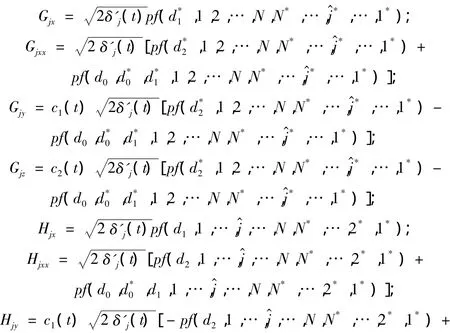
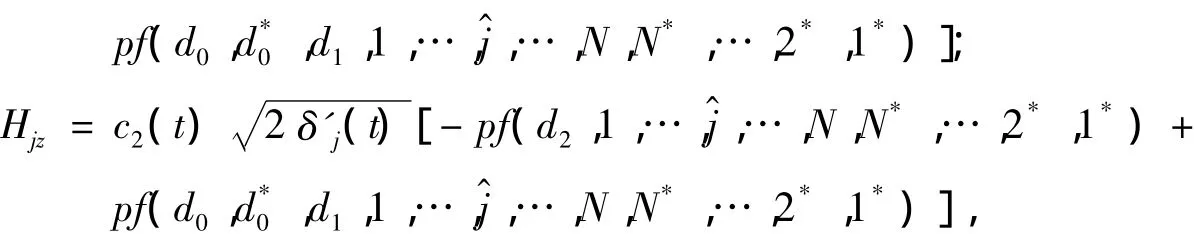
把以上微分公式代入双线性方程(9)中，得到K+1个pfaff恒等式，

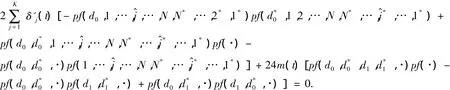
由此说明函数 f，Gj，Hj满足双线性方程(9)．

类似地，可以证明函数f，Gj，Hj满足双线性方程(10)～(13)．

方程(9)～(13)就构成了双线性的带自相容源的变系数(3+1)维KP方程，而式(6)～(8)中的函数f，Gj，Hj就是方程(9)～ (13)的行列式解．

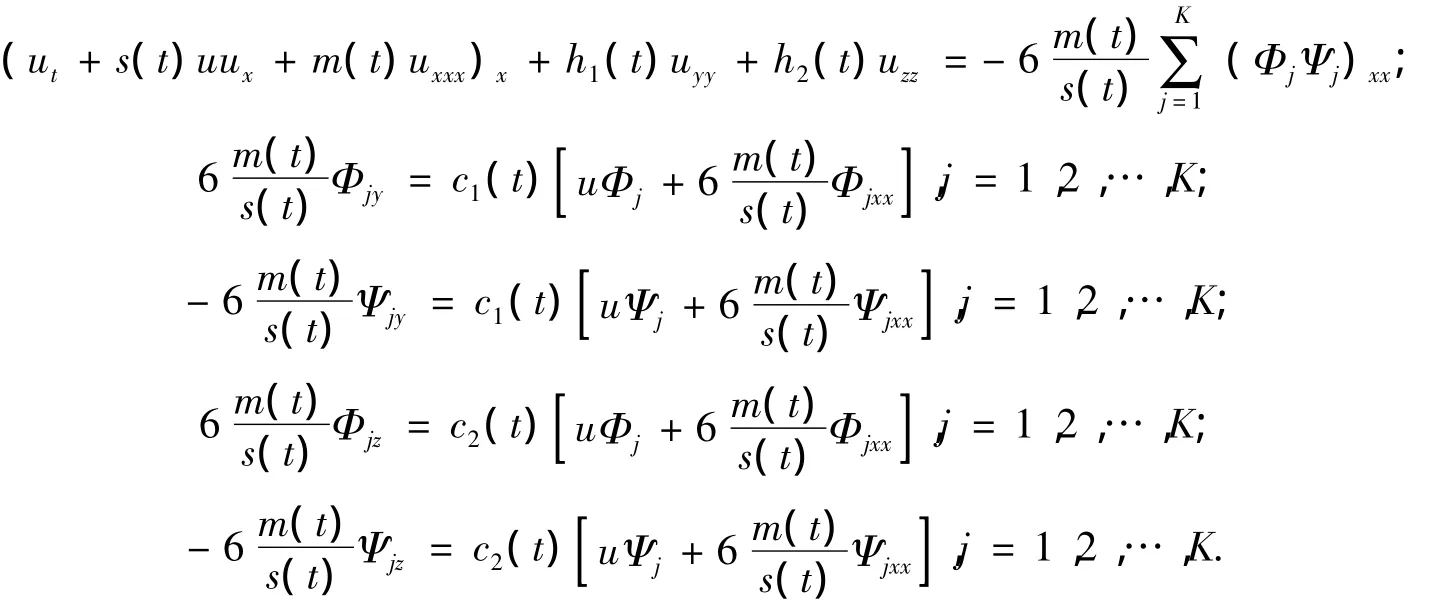
则式(9)～(13)就转化为非线性发展方程:此方程即是带自相容源的变系数(3+1)维KP方程．

2 带自相容源的变系数(3+1)维KP方程的双线性B¨acklund变换

定理2 双线性带自相容源的变系数(3+1)维KP方程(9)～(13)有双线性形式的acklund变换，

证明 为证明该定理，只需证明当函数f，Gj，Hj满足方程(9)～(13)时，满足方程(14)的函数f'，G'j，H'j也满足方程(9)～(13)，事实上:

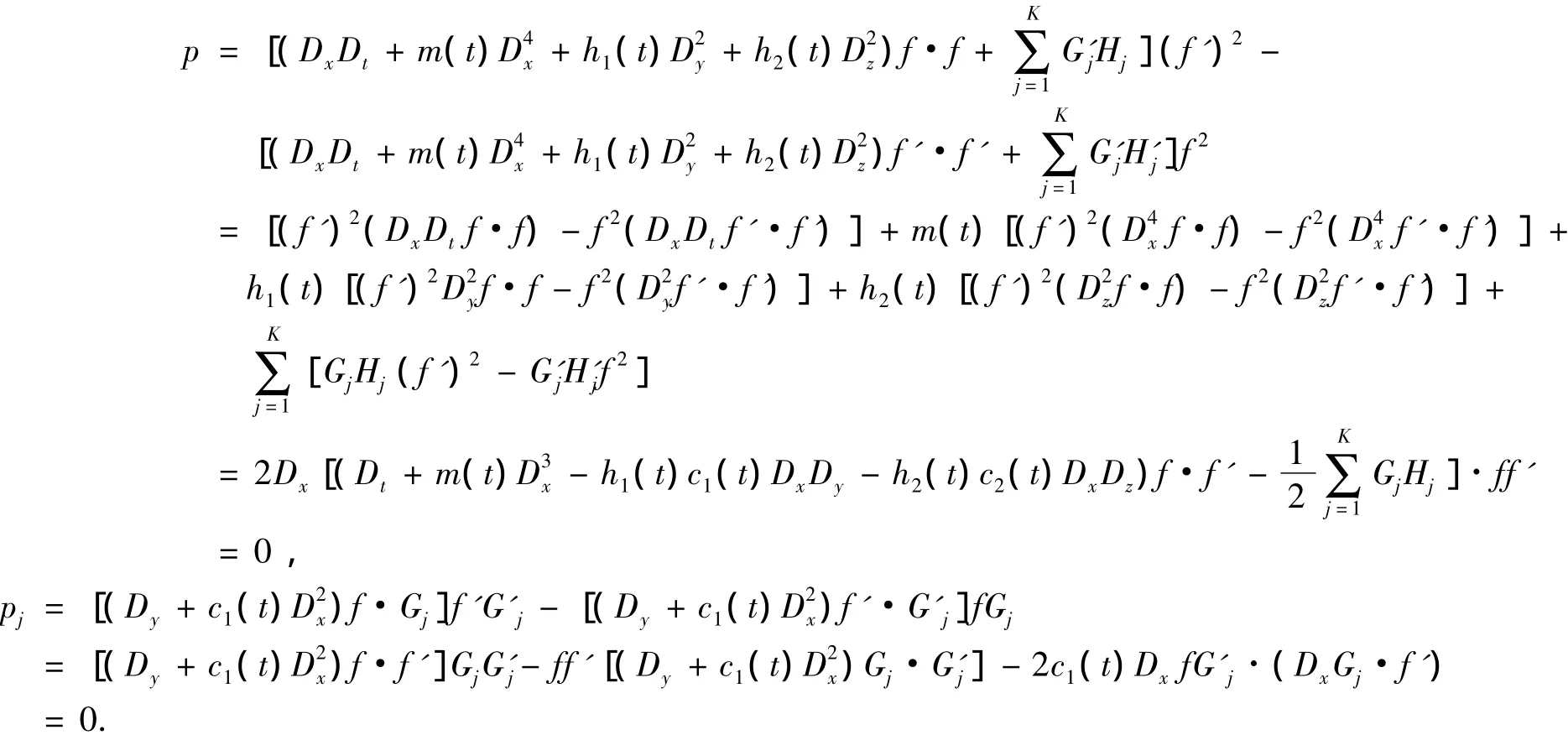
因此，证明了函数f'，G'j，H'j满足双线性方程(9)～(13)，故式(14)是带自相容源的变系数(3+1)维KP方程的双线性B¨acklund变换．

［1］ Hu Xingbiao，Wang Hongyan.New type of KP equation with self-consistent sources and its bilinear Bäcklund transformation［J］.Inverse Problems，2007，23(4):1433-1444.

［2］ Wang Hongyan，Hu Xingbiao，Tam H W.A(2+1)-dimensional Sasa-Satsuma equation with self-consistent source［J］.J Phys Soc Jpn，2007，76(2):024007.

［3］ 王红艳，胡星标.带自相容源的孤立子方程［M］.北京:清华大学出版社，2008:16-21.

［4］ 王鸿业，温丹华.一个带自相容源的(3+1)维KP方程［J］.郑州大学学报:理学版，2012，44(4):6-9.

［5］ 徐娟.变系数维KP方程的Wronskian和Grammian解［J］.温州大学学报:自然科学版，2013，34(1):13-17.

［6］ 孟祥华.基于符号计算的光纤通信等若干领域中变系数非线性模型的研究［D］.北京:北京邮电大学，2009:124-125.