基于常微分方程的周口市人口增长预测
2014-03-19欧阳瑞张丽娟
欧阳瑞,张丽娟
(周口师范学院 数学与统计学院,河南 周口466001)
周口市位于河南省东南部,素有“华夏先驱,九州圣迹”之美誉.但人口问题始终是制约周口经济持续健康发展的重要因素.周口长期处于人口基数大,低增长率与高增长量并存的状况.为更好地促进和规划周口未来的发展,笔者调查统计了过去几十年的人口总数,运用matlab软件进行编程计算,通过Logistics人口模型和Malthus人口模型,对周口市未来几十年的人口发展趋势进行预测,并对两种模型的优劣进行对比.
1 基于常微分方程的人口预测模型
预测人口的模型有很多,各自有不同的特点及优势,笔者采用最基本的马尔萨斯(Malthus)模型和阻滞增长(Logistics)模型.
1.1 模型基本假设
结合实际情况,若要准确预测周口未来的人口数量,必须考虑一些影响人口的因素.根据文献[1]和[2],先设定假设条件如下:
1)周口长期处于一个和谐稳定的状态;
2)周口没有任何重大的暴力活动及自然灾害的发生;
3)长期内无毁灭性的疾病发生;
4)人口的迁入和迁出基本平衡,即人口的迁移问题可忽略不计;
5)生育和死亡状况不发生显著地变化.
1.2 模型介绍
1.2.1 马尔萨斯(Malthus)模型
假设在人口自然增长的过程中,净相对增长率(单位时间内人口的净增长数与人口总数之比)是常数,记此常数为r(也称为生命系数).在t到t+Δt这段时间内人口数量N=N(t)的增长量为N(t+Δt)-N(t)=rN(t)Δt,于是N(t)满足微分方程

如设初值条件为
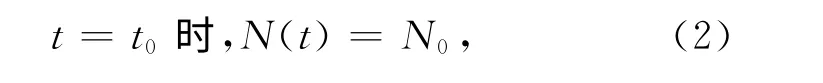
求解可得方程(1)满足初值条件(2)的解为

如果r>0,上式说明人口总数N(t)将按照指数规律无限增长.将t以1年或10年为单位离散化,那么就可以说,人口总数是以er为公比的等比数列增加的.
当人口总数不大时,生存空间、资源等极充裕,人口总数呈指数的增长是可能的.但当人口总数非常大时,指数增长的线性模型则不能反映这样一个事实:环境所提供的条件只能供养一定数量的人口生活.所以Malthulst模型在N(t)很大时是不合理的.
1.2.2 阻滞增长(Logistics)模型
荷兰生物学家Verhulst引入常数Nm(环境最大容纳量)表示自然资源条件所能容纳的最大人口数,并假设净相对增长率为即相对增长率随N(t)的增加而减少,当N(t)→Nm时,净增长率→0.按此假设,人口增长的方程应该修正为

设初值条件t=t0,N=N0,则其解为

这就是Logistics模型.当Nm与N相比很大时与rN相比可以忽略,则模型变为Malthus模型;但当Nm与N相比不是很大时这一项就不能忽略,人口急剧增加的速率就要缓慢下来.
2 利用两种模型,进行人口预测
首先进行调查,得到周口近十几年的数据如下所示:
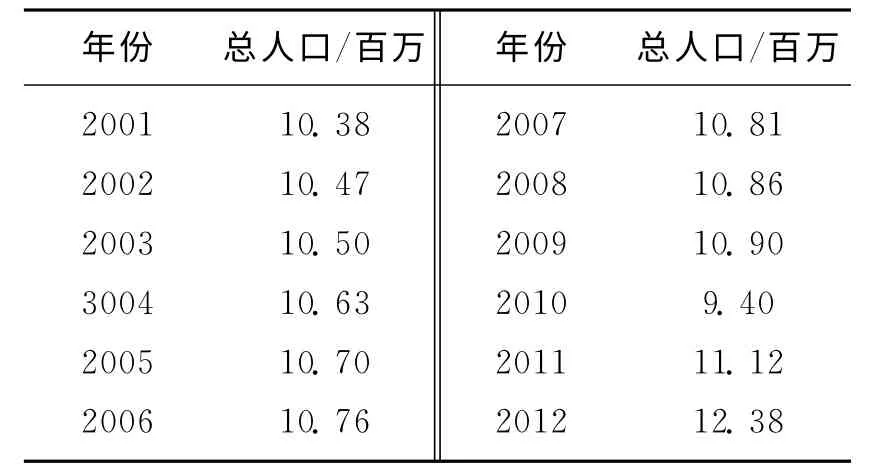
表1 周口市近12年人口统计数据表
下面用上述的两种模型分别对周口市未来几十年的人口发展趋势进行预测.程序中选择的是以2001年的人口数为N0.
2.1 Malthus模型预测结果
首先用Malthus模型进行预测,取人口的自然增长率r=0.029[6],利用matlab软件进行编程运算,得到的结果如表2.

表2 Malthus模型预测周口市各年份总人口数
根据上述预测数据,再次利用matlab软件进行编程画出Malthus模型预测的周口市人口增长趋势图如图1.
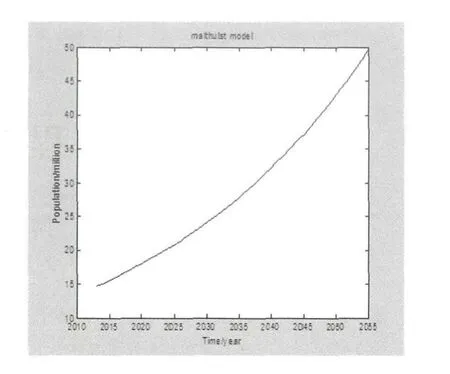
图1 Malthus模型预测人口增长趋势图
由表1的预测数据和增长趋势图可知,在环境条件绝对理想的条件下,若环境的容纳量无限大时,人口是持续无上限的增长的,Malthus模型的预测结果是呈指数增长的,这显然是不符合实际情况的,因为自然资源并不是可以无限索取利用的.
2.2 Logistics模型预测结果
由表1中的数据经计算得出周口市的人口平均增长率为0.58%.利用统计数据中2012年的人口数量,由Logistics模型式(4),有
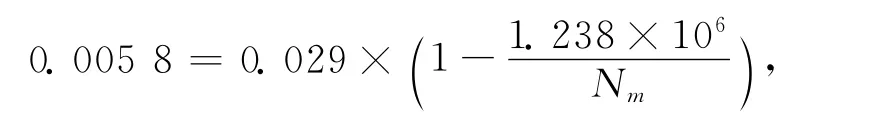
所以由Logistics型可得出Nm=1.5475×107,则对应的Logistics模型中时刻t的人口数量为
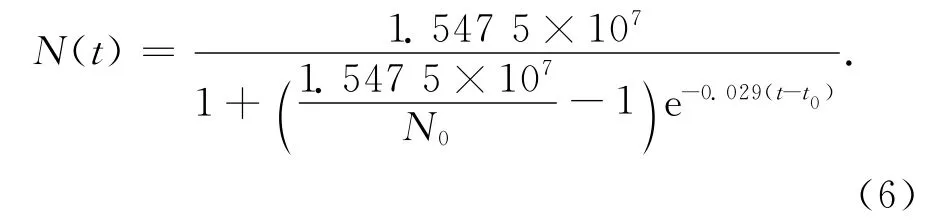
由上可知周口的最大人口容纳量Nm=1.5475×107,当人口数趋近这个数量时,就会超过环境的负荷,这时无论是对周口市的经济还是以后的长久发展,必定会产生不良影响.
下面采用Logistics模型进行预测,同样利用matlab软件进行编程,得到的结果见表3.
根据上述预测数据,可以画出Logistics模型预测的周口人口增长趋势图如图2.
观察图2,可以清楚地看到,Logistics模型预测的人口增长趋势明显变缓,正是由于有了最大人口容纳量Nm的限制,控制了人口的迅猛增长,当人口数越接近Nm时,增长速度越慢.到一定的时候,人口将会实现零增长甚至是负增长.而且由于考虑了实际环境的最大容纳量,这样预测的数据将更加准确合理,更符合实际.

表3 Logistics模型预测周口各年份总人口数

图2 Logistics模型预测人口增长趋势图
这里所讨论的模型,都是在理想情况下进行的,所以在进行预测的时候有很多影响人口发展的因素还未考虑,因此Logistics模型仍不是很完美.在实际社会中,影响人口变化的因素往往很多,像老龄化进程加速、出生人口性别比持续增高、乡镇人口城镇化、年龄结构、计划生育等以及本文中假设的情况,都可以影响人口数量的发展.若想更准确地预测未来的人口,需将这些因素加以考虑.
3 结束语
一个地区的人口总量对当地经济社会发展会产生重要影响,因此准确的人口预测对未来经济、社会的发展将会起到非常重要的作用.通过笔者得到的周口市人口增长趋势预测数据,可以对周口市的未来经济社会发展进行更好的规划,使经济发展更适应社会人口实情;通过对人口增长趋势的了解,还可以适当地调整经济增长的方式和速度,能更好地控制人口的数量,实现资源的优化配置.
[1]姜启源,谢金星.数学模型[M].北京:高等教育出版,2003:100-23 4.
[2]朱道元.数学建模精品案例[M].南京:东南大学出版社,2003:98-156.
[3]穆红霞,周克元.中国人口增长预测数学建模研究[J].牡丹江教育学院学报,2008(6):96-97.
[4]李永胜.人口预测中的模型选择与参数认定[J].财经科学,2004,11(2):24-28.
[5]张红芹.微分方程在人口预测中应用[J].吉林省教育学院学报,2011,27(10):60-61.
[6]王高雄,周之铭,朱思铭.常微分方程[M].3版.北京:高等教育出版社,2004:219-240.
[7]董永权.中国人口增长预测[J].唐山师范学院学报,2009,31(2):46-48.
[8]冯守平.中国人口增长预测模型[J].安徽科技学院学报,2008,22(6):73-76.
