基于空域互相关矩阵的声源延时估计方法

舒雪姣，黄根岭，李冬梅

（1.中兴通讯学院，深圳518083；2.郑州铁路职业技术学院，郑州450052；3.郸城财鑫糖业有限责任公司，河南 郸城477150）

声源定位技术是利用传声器拾取语音信号，并用数字信号处理技术对其进行分析和处理，继而确定和跟踪声源的空间位置的一种技术.根据声音信号的特征以及声源所处环境，涌现了各种各样的定位方法，但由于混响、噪声等一系列影响声源信号质量的因素存在，使得现有的声源定位算法不能取得较好的定位效果［1，2].针对这一问题，笔者主要研究了基于麦克风阵列的声源定位方法.

麦克风阵列信号处理是将多个麦克风传感器布置在空间中不同的位置，组成传感器阵列，并利用此阵列接收、处理空间信号，提取所接收的信号及其特征信息.麦克风阵列信号处理通常采用空域和时域（或频域）结合的办法进行处理［3].

笔者通过系统地研究基于麦克风阵列的声源定位方法，利用阵列信号处理和DOA估计技术实现目标声源的定位，提出了一种基于空域互相关矩阵的延时估计方法，并通过仿真实验验证该方法的可靠性.

1 时延估计原理

利用麦克风阵列对声源进行定位，其基本思想就是根据估计出的各通道信号之间的时间延迟来确定目标的方位和距离.基于时延估计的声源定位方法计算量相对较小，利于实时处理.不仅如此，基于时延的声源定位方法还具有较高的定位精度，因此在现有的声源定位系统中占有很大的比重［3，4].其算法原理如下：

假定信号在信道中以无色散球面波的方式传播，为了简化分析和研究，通常将信号源和接收器考虑在同一个平面中，从而将问题化简为二维定位问题.在二维空间中，球面波退化为柱面波.如图1所示，由于信号到达两个传声器的路径不同，将会相隔一段时间差，这段时间差称为时延.而波阵面到达两个传声器之间的距离差称为声程差，等于介质中声音传播速度与时延的乘积.

图1 时延产生过程示意图

假设声源与传声器距离较远，符合远场条件，则它辐射的信号可以看作是以平面波的形式传播，如图2所示.

图2中L为两传声器之间的距离，D表示信号到达两传声器之间的时延，C表示声速，H为声程差，则根据几何关系可知，声源相对于传声器阵列的方向角为：

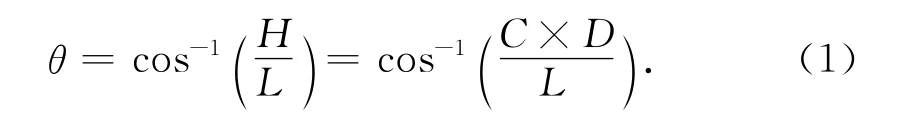
因此由时延D，就可以计算出方位角θ.

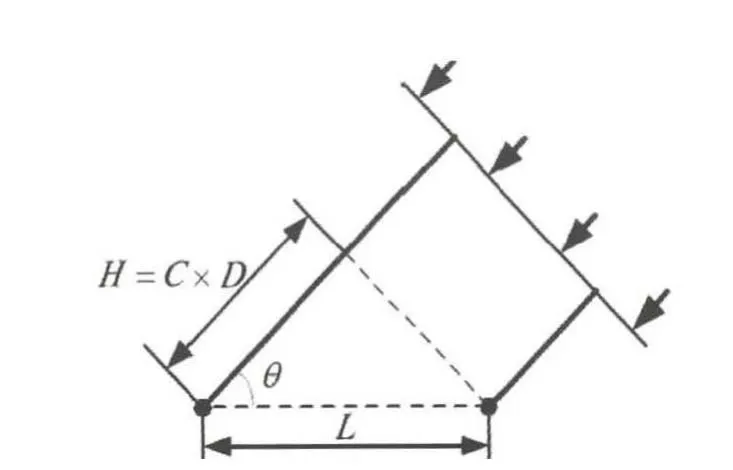
图2 远场情况下时延估计原理图

对图2所示的被动定位系统，在无混响影响且相关噪声较弱的情况下，有如下理想数学模型：

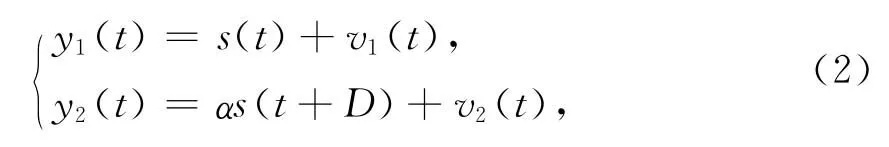
式（2）中，y1（t）和y2（t）分别为两传声器的接收信号，s（t）为声源信号，D为两传声器之间的相对时延，α是声波相对衰减系数，v1（t）和v2（t）是两传声器接收到的加性噪声，且假设v1（t），v2（t）和s（t）为互不相关的平稳随机过程.

时延估计根据不同位置接收器所接收到的同源信号，估计出其中所包含的时延信息，即估计D的问题.时延估计的精度越高，定位误差就越小，每种时延估计方法各有利弊，应根据具体情况，结合精度要求和运算量限制进行选择［5].

2 空域互相关矩阵时延估计方法

笔者以空域互相关矩阵为基础，提出一种切实可行的延时估计方法，该方法原理简单、直观，运算量适中，在一定条件下能够实时实现.仿真实验表明，该方法能够取得精确的延时估计值，同时满足实时性的要求.

2.1 算法原理

假设单声源自由场模型中有一N个麦克风组成的均匀线阵（N≥2）.忽略噪声信号，则第n个麦克风接收到的信号为

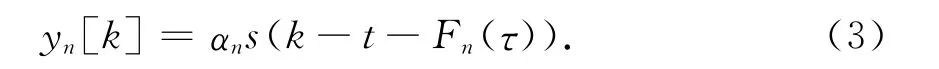
其中，t为信号传播时间，Fn（τ）为第n个麦克风相对于第一个麦克风的延时时间.由上式可以得到：

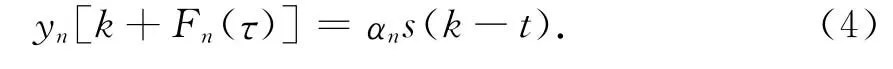
根据上式，定义一信号矢量：

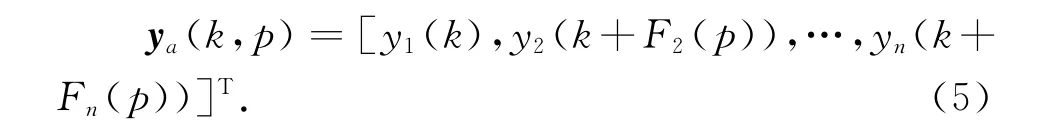
则有：

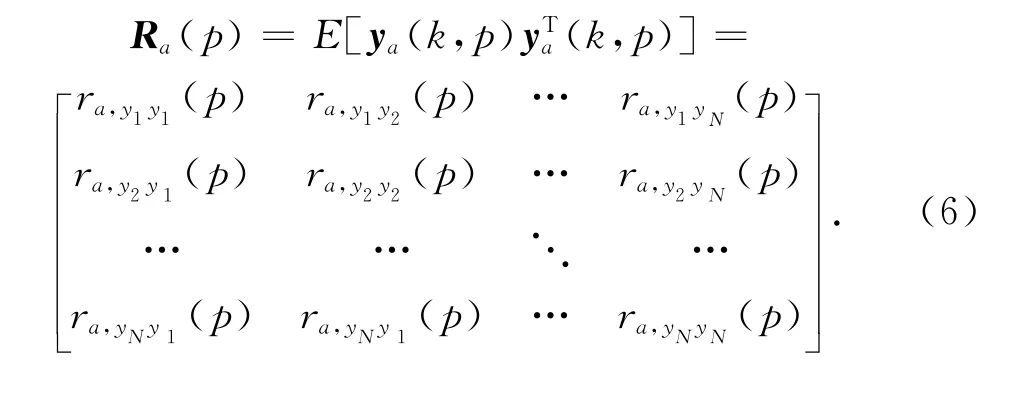
此 处，ra，yiyj（p）＝E［yi（k＋Fi（p））yj（k＋Fj（p））]，i，j＝1，2，…，N.

上式即为空域形式的互相关矩阵.该空域互相关矩阵又可被分解为如下形式：

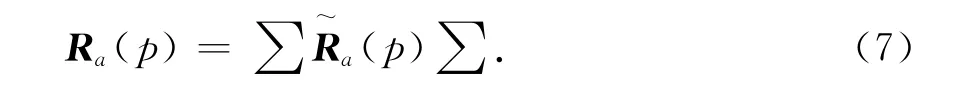
此处

其中

表示第i个麦克风与第j个麦克风接收信号之间的互相关系数.

由式（9）可以看出，矩阵~Ra（p）是对称的，半正定的，并且所有对角线元素均为1，由矩阵理论可以得出：

假如N＝2，则有：

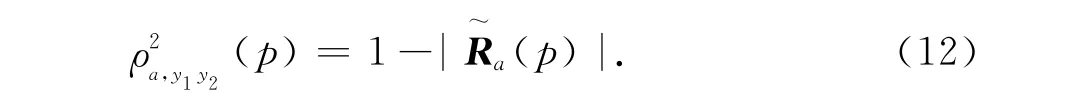
（p）表示第1个麦克风与第2个麦克风接收

信号之间的互相关系数的平方，由此定义：

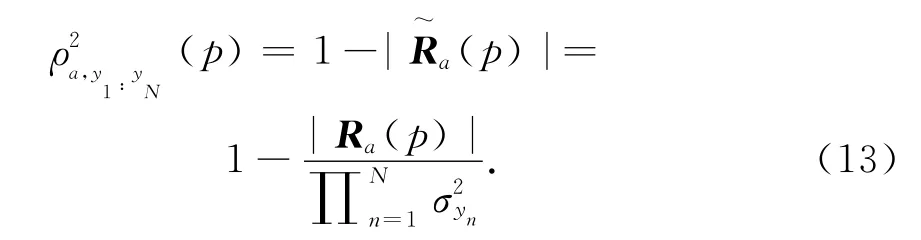
上式表示所有N个通道信号的互相关性大小.

根据式（13），延时估计如下所示：

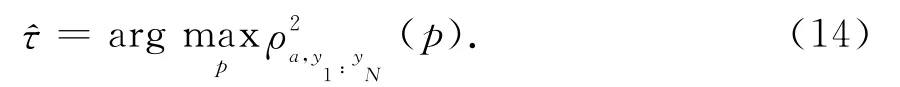
上式等同于计算：

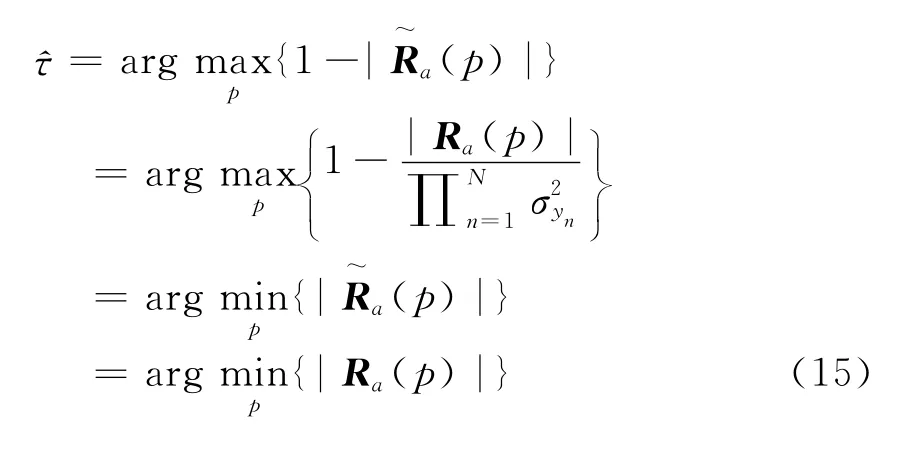
2.2 算法仿真及结果

2.2.1 实验条件

为了能够模拟真实带混响的声源环境，使用IMAGE［6]模型产生房间和麦克风之间的脉冲响应序列，混响是指在语音信号传播中，由于反射、衍射等原因，到达传声器的语音信号除了直达信号外还存在着多条其他路径传来的信号，从而使接收信号的幅度衰减、音质变差的现象.实验中假设房间为长方体形，每一墙面具有相同的反射系数，且认为该系数与声源位置和频率无关.

实验设置如下：

1）房间尺寸大小：6m×4m×3m（长×宽×高）；

2）房间墙面反射系数ri（i＝1，2，…，6）为0.5；

3）麦克风阵列位置：本实验采用一8理想阵元均匀线形麦克风阵列，各个麦克风均为全向型.设置第一个麦克风坐标为（3，2，0），相邻麦克风之间的距离为0.17m；在本次试验中设定相邻麦克风接收到信号延时大小为16个采样间隔；

4）声源位置：在（4，3.714，2）位置处放置一全向型点状声源信号，该声源为16kHz采样的语音信号，且假设声源处于远场；

5）对语音序列进行分帧加窗处理，设定每一帧信号长度为2048个采样值；窗函数设定为2048长度的汉宁窗；

6）采用静音检测VAD（voice activity detector）技术区分一帧信号是否为静音信号；

7）最后利用式（9）得到每一帧信号的空域互相关矩阵，并计算矩阵行列式大小，从而估计出相应延时；若该帧信号为静音信号，则该帧在计算过程中将会被忽略；仿真结果将与GCC-SCOT算法和LMS自适应算法进行比较.

2.2.2 实验结果

使用IMAGE模型仿真房间和麦克风之间的脉冲响应序列如下图所示：

图3 房间和麦克风之间的脉冲响应序列图

实验一：无混响情况下，SNR为10，0，-5dB和-10dB时的延时估计仿真.

本实验分别计算了麦克风数为2，4和8时，基于空域互相关矩阵延时估计值，并在相同条件下对GCC-SCOT延时估计算法和LMS自适应延时估计算法也进行仿真，以与基于空域互相关矩阵延时估计算法对比，实验结果如下图所示：

1）SNR＝10dB时，仿真结果：

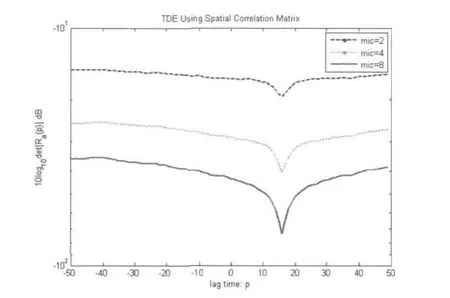
图4 空域互相关矩阵延时估计算法图

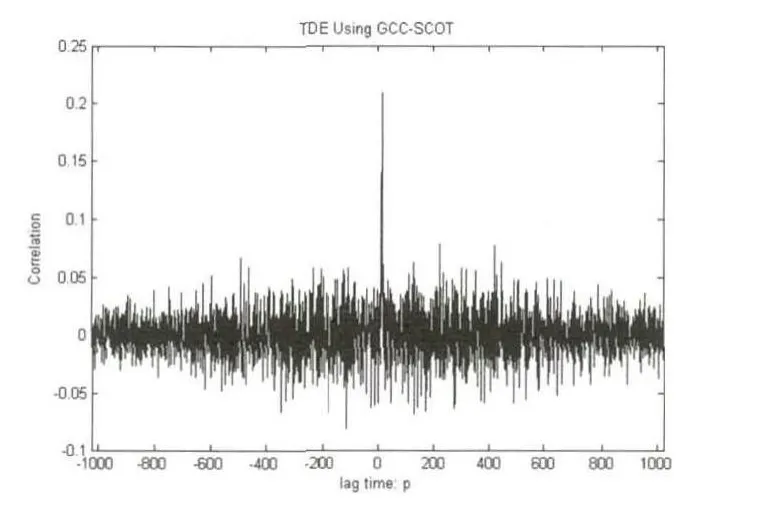
图5 GCC-SCOT延时估计算法图

2）SNR＝0dB时，仿真结果：

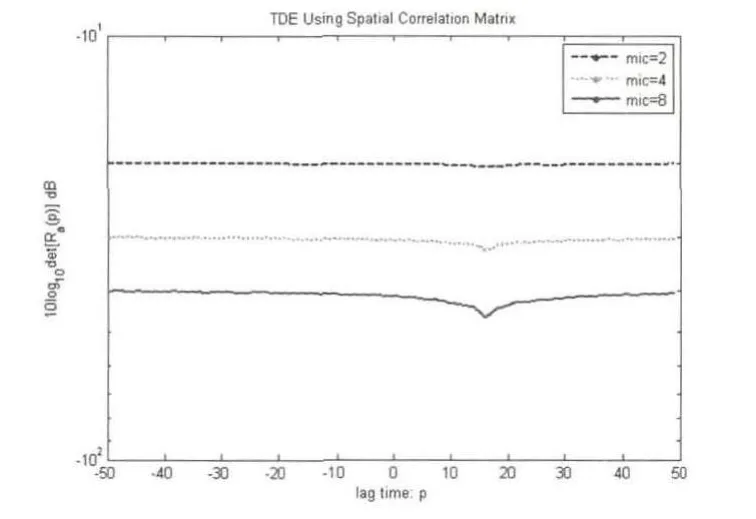
图6 空域互相关矩阵延时估计算法图

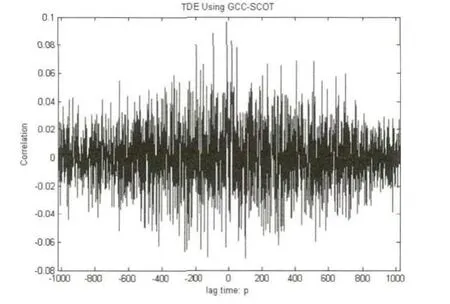
图7 GCC-SCOT延时估计算法图

3）SNR＝-5dB时，仿真结果：

图8 空域互相关矩阵延时估计算法图

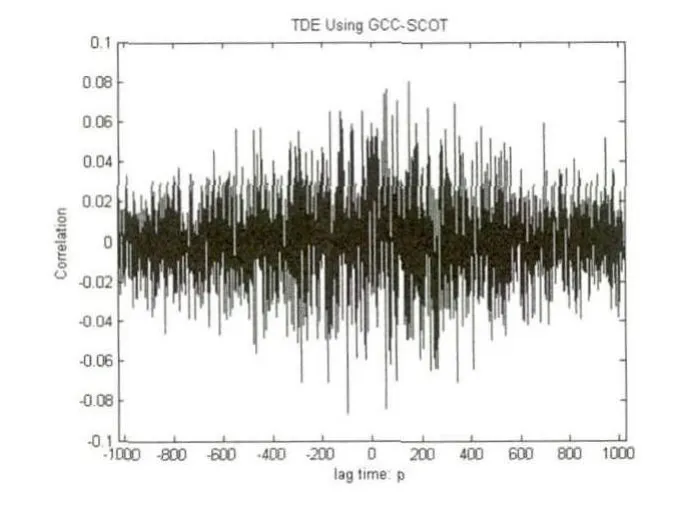
图9 GCC-SCOT延时估计算法图

4）SNR＝-10dB时，仿真结果：

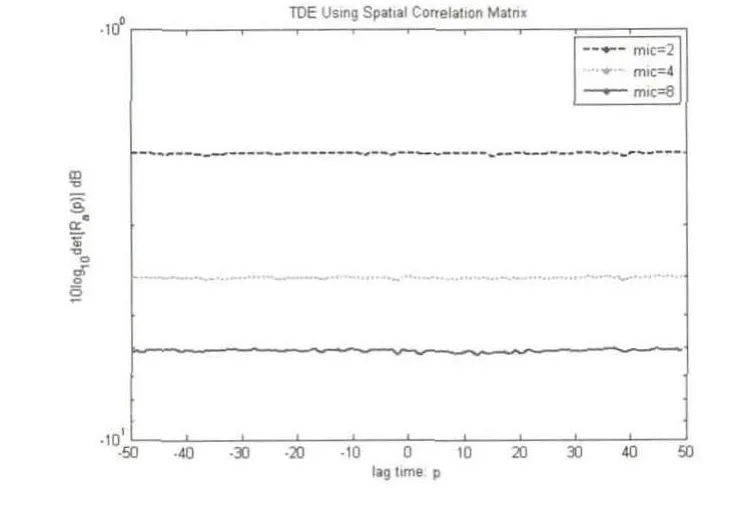
图10 空域互相关矩阵延时估计算法图

实验二：混响情况下，SNR为10，0，-5dB和-10dB时的延时估计仿真.

本实验分别计算了麦克风数为2、4和8时，基于空域互相关矩阵延时估计值，并在相同条件下对GCC-SCOT延时估计算法和LMS自适应延时估计算法也进行仿真，以与基于空域互相关矩阵延时估计算法对比，实验结果如下图所示：

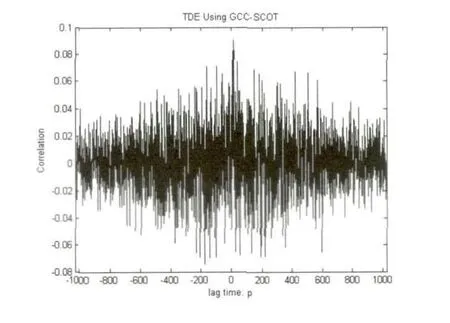
1）混响情况下，SNR＝10dB时，仿真结果：

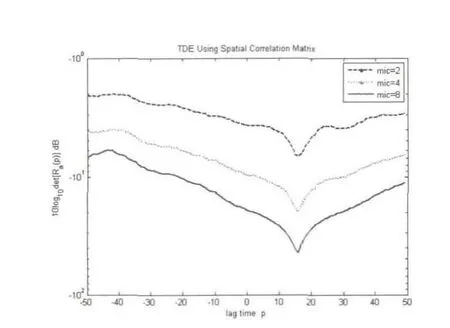
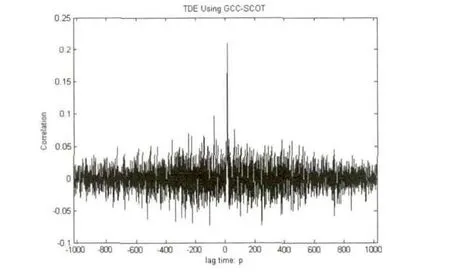
图13 GCC-SCOT延时估计算法图

2）混响情况下，SNR＝0dB时，仿真结果：

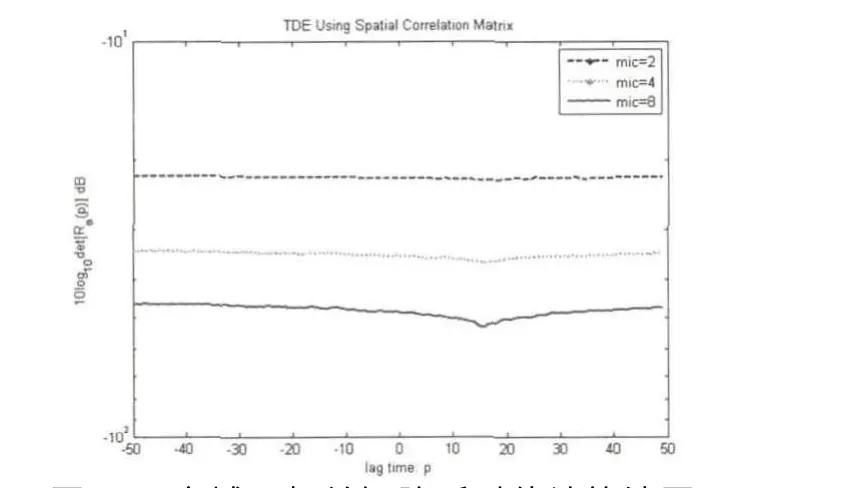
图14 空域互相关矩阵延时估计算法图

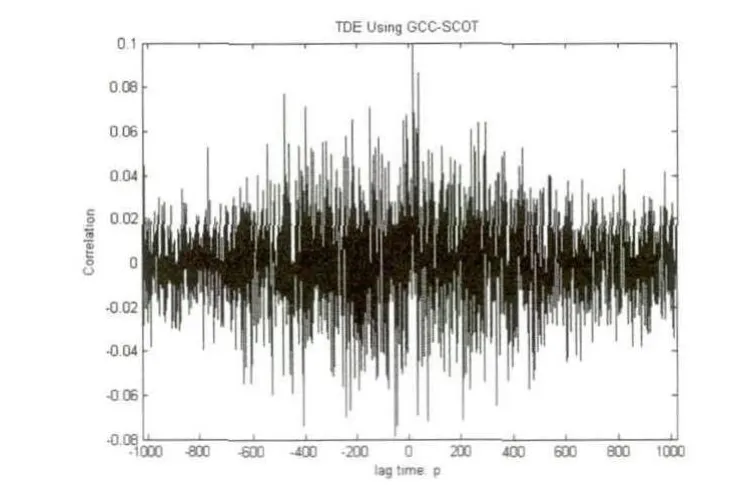
图15 GCC-SCOT延时估计算法图

3）混响情况下，SNR＝-5dB时，仿真结果：

图16 空域互相关矩阵延时估计算法图

图17 GCC-SCOT延时估计算法图

4）混响情况下，SNR＝-10dB时，仿真结果：

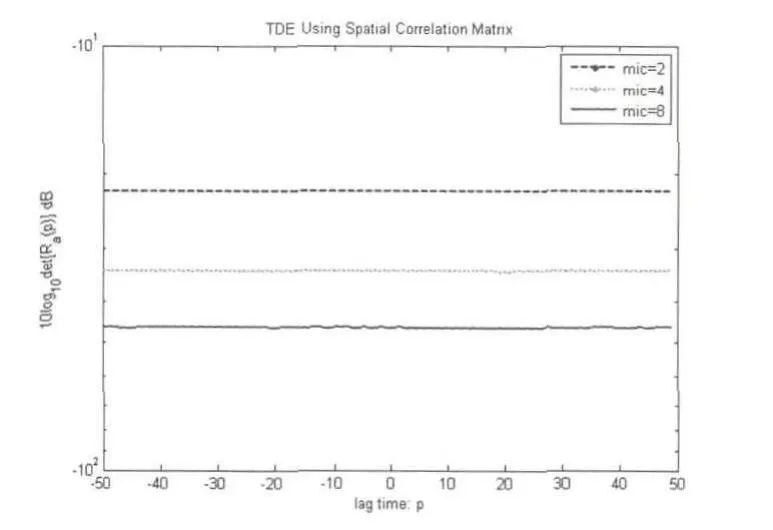
图18 空域互相关矩阵延时估计算法图

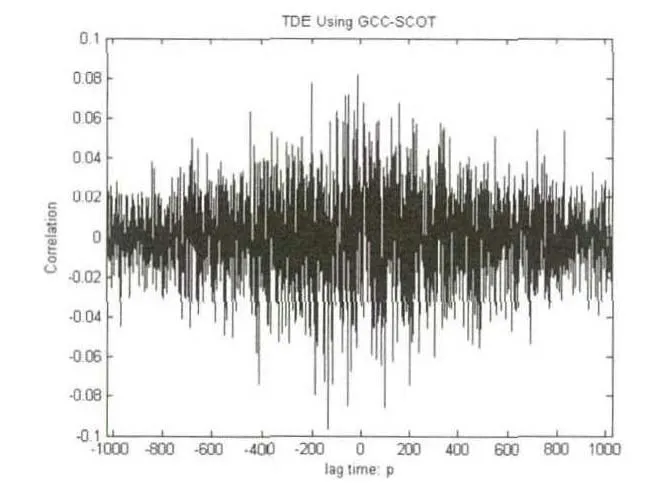
图19 GCC-SCOT延时估计算法图

2.2.3 实验结论

从上面两个实验中可以看出，基于空域互相关矩阵的延时估计算法的性能同GCC-SCOT延时估计算法一样，主要受到信噪比和混响大小的影响.两种试验情况得到的结果类似.SNR为10dB时，两种延时估计算法均能正确的估计出延时大小，此时，GCC-SCOT最大值尖峰明显，基于空域互相关矩阵的延时估计算法最小值尖峰很明显；当信噪比降到0dB时，基于GCC-SCOT延时估计算法以及2阵元的基于空域互相关矩阵延时估计算法得到的延时估计不准确，而基于空域互相关矩阵延时估计算法的4阵元和8阵元麦克风阵列依然能得到准确的延时估计值，此时2阵元空域互相关矩阵延时估计算法最小值尖峰退化，而4阵元与8阵元最小值尖峰较明显；当SNR为-5dB时，只有基于空域互相关矩阵延时估计算法的8阵元麦克风阵列能得到准确的延时估计，此时2阵元和4阵元空域互相关矩阵延时估计算法最小值尖峰退化，而8阵元最小值尖峰相对较明显；当SNR为-10dB时，各算法均不能得到准确的延时估计，此时2阵元、4阵元和8阵元空域互相关矩阵延时估计算法最小值尖峰全部退化.

根据上述两次实验可以得出，4阵元与8阵元的基于空域互相关矩阵延时估计算法性能优于GCC-SCOT延时估计算法，主要体现在能够在低信噪比和存在混响的情况下得到准确的延时估计.对于基于空域互相关矩阵的延时估计算法来说，在信噪比较低和混响存在的情况下，可以通过增加阵列的阵元数目来取得理想的延时估计效果，但这样做又会使算法的计算量增加.为了既能得到准确的延时估计，又能使算法运算量处于一较低水平，则应该在计算空域互相关矩阵之前提高采集信号的信噪比大小.

3 总结

基于空域互相关矩阵提出了一种新型的延时估计方法，该方法随着麦克风阵列数目的增加可以得到准确的延时估计，并且在信噪比不太低的情况下也能获取精确的延时估计.笔者所提出的算法运算量适中，在阵元数目不多的情况下可实现实时的延时估计.若对于实时性要求不高，则笔者所提出的算法可以通过增加阵元数目得到精确的延时估计.此外，随着阵元数目的增加，该算法对混响的抑制能力也会逐步增强.

［1]Don H.Johnson，Dan E.Dudgeon.Array Signal Processing-Concepts and Techniques［M].Beijing：Prentice-Hall，1993.

［2]王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M].北京：清华大学出版社，2004.

［3]Benesty J，Chen J，Huang Y.Microphone Array Signal Processing［M].Berlin：Springer，2008.

［4]鲁佳.基于传声器阵列的声源定位研究［D].天津：天津大学硕士学位论文，2008.

［5]Li D.，Dong C.，Huang J..A study on the application of Toeplitz approximation method on DOA e-stimation［C]／／2nd International Conference on Signal Processing Systems（ICSPS），Dalian China，2010（3）：215-218.

［6]Allen J.B.，Berkley D.A..Image method for efficiently simulating small room acoustics［J].Journal of Acoustical Society of America，1979，65（4）：943-950.

［7]陈可，汪增福.基于声压幅度比的声源定位［J].计算机仿真，2004，21（11）：443-449.

［8]柯昆.声源定位技术研究［D].西安：西安电子科技大学硕士学位论文，2010.