时域仿真分析下的应用型控制理论教育教学研究

刘 琪，刘晓青

（周口师范学院 物理与机电工程学院，河南 周口466001）

控制理论包括经典控制理论和状态空间理论两部分内容，有的高校将之合并设置为“自动控制理论”，也有的高校将之分别设置为“自动控制原理”和“现代控制理论”.控制理论研究的中心问题是系统在控制中的性能，是研究自动控制系统的普适方法论.控制理论是自动化专业的核心主干课程，也是电子信息工程、电气工程及其自动化等工学电类专业的必修课.

现有科学计算发展水平使直接求取高阶系统的特征根变得非常简单，然而因控制理论发展初期受传统数学理论影响，很多学者至今仍认为高阶系统对应的高阶代数方程很难求出其所有特征根［1].在实际教学中，往往借助Laplace变换求解系统响应，Laplace变换计算量较大，步骤烦琐，冲淡了控制理论课程的中心问题，也容易使学生失去学习课程的兴趣［2-4].

近年来，高等教育日益大众化，中国的转型发展和产业升级需要大量的应用型人才，这对自动化类专业人才培养模式提出新的要求和挑战.将控制理论研究的主要对象——线性定常系统摆在更突出的位置，在教学中引入MATLAB，通过恰当的时域仿真应用［5]，降低教学难度，凝练教学主题，提高学生兴趣，提升教学效率，是控制理论教学的有益尝试.

1 解析解法

线性定常系统的解析解是控制系统输出的准确数学表达，MATLAB的强大科学计算能力可简便地得到输出的数字特征.

1.1 传递函数的解析解法

线性定常系统的传递函数一般表示为

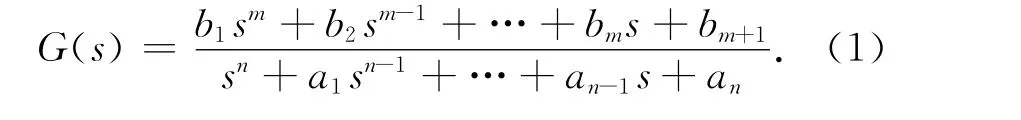
在输入信号为U（s）的作用下，其输出表达式为

将输出按部分分式展开，式（2）可改写为

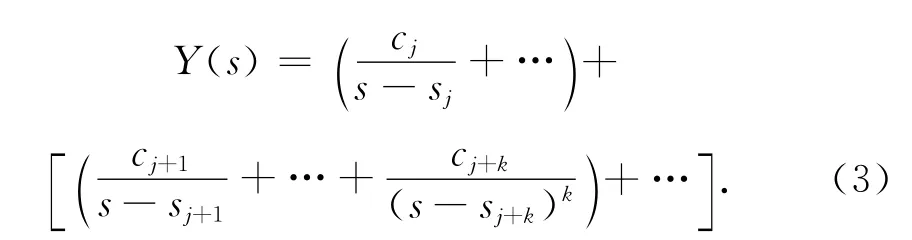
式（3）中sj表示j个非重根，sj＋1是k重根，Y（s）共n项.将式（3）进行Laplace变换得到

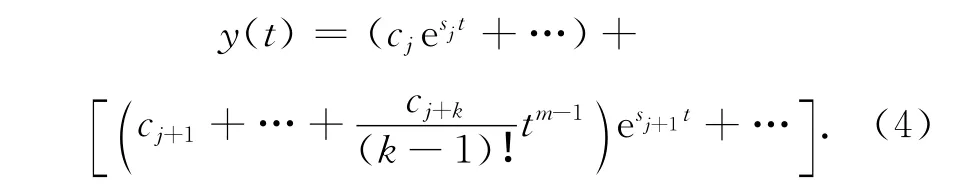
MATLAB可用residue（）函数求解特征根sj，sj＋1，并可显示j，k数目，由这些值可以写出系统的解析解.其调用格式是［r，p，K]＝residue（num，den）.

1.2 状态模型的解析解法

线性定常系统的状态模型一般表示为

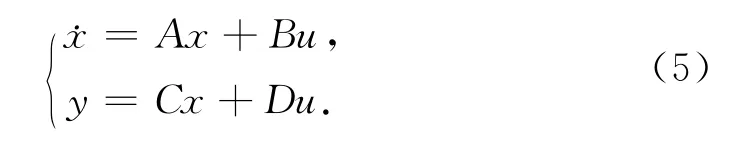
在输入信号为u（t）的情况下，其输出表达式为

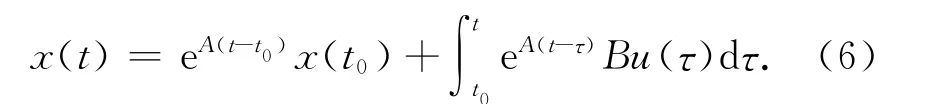
在式（6）中，积分项并不好处理，可以定义附加变量如式（7）所示

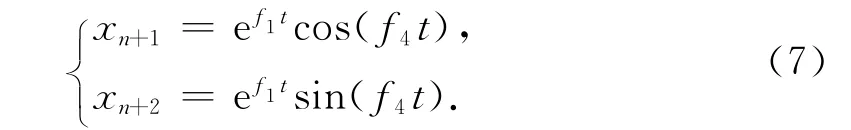
在通用条件下，假定输入信号为典型信号

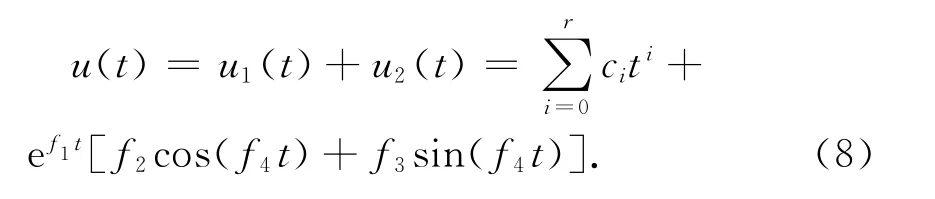
可构造增广状态模型

由式（9）可得状态模型的内部状态解析解为

则状态模型的外部输出解析解为

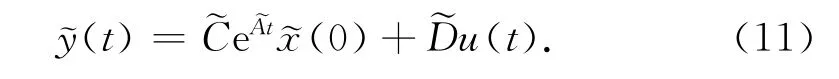
2 典型系统的数字仿真

2.1 系统的阶跃响应指标

典型的阶跃响应曲线如图1所示，控制理论研究中关注的性能指标主要有：

（1）稳态值

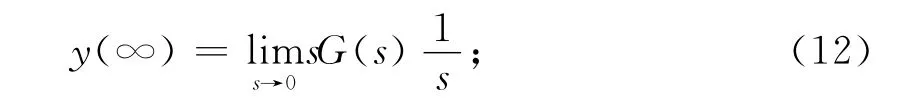
（2）超调量

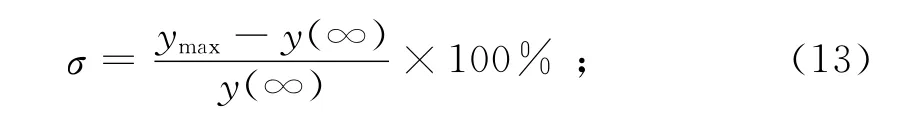
（3）调节时间ts.

2.2 典型的二阶系统仿真

二阶系统是具有典型代表的线性定常系统，其研究和教学具有重要的理论和现实意义，典型的单位负反馈二阶系统如式（14）所示，其中ζ为系统的阻尼比，ωn为系统的无阻尼自然振荡频率.系统框图如图2所示.

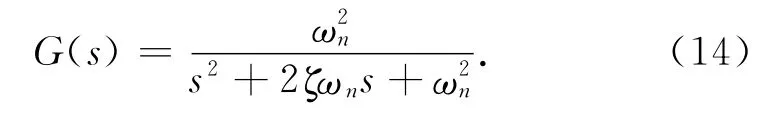
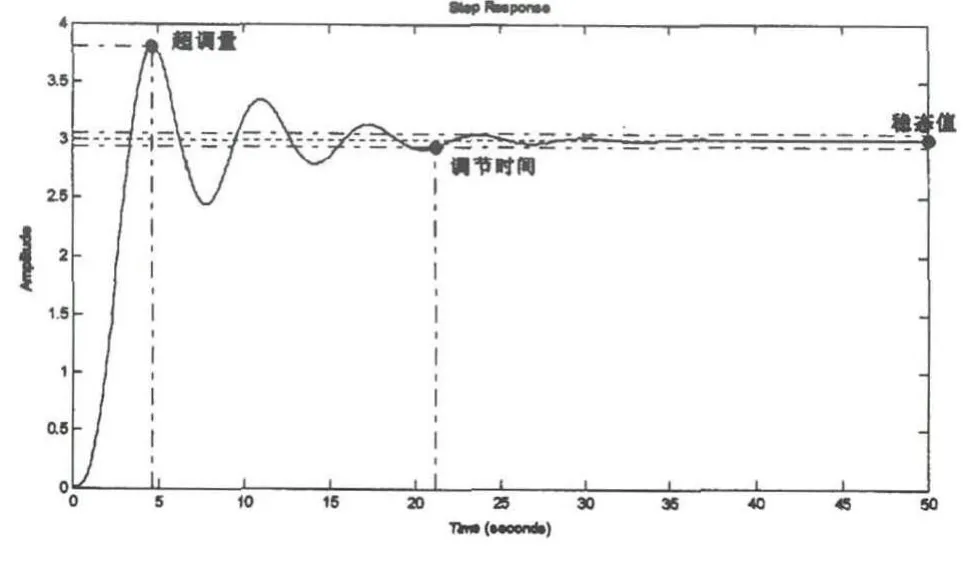
图1 系统的阶跃响应指标图

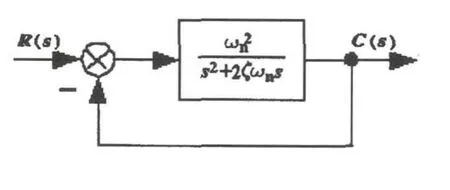
图2 典型二阶系统框图

根据线性系统解析解的理论，其阶跃响应y（t）的解析解的一般形式为

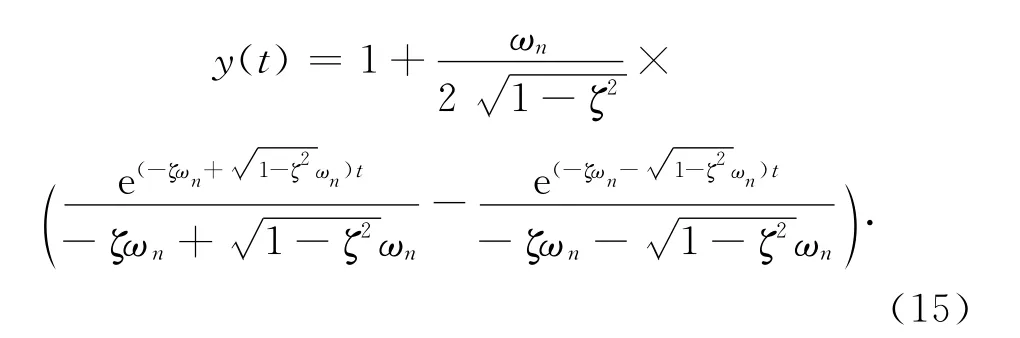
系统的阻尼比ζ的取值范围不同，系统的响应表达式不同：

（1）当ζ＝0时，则系统的响应表达式如式（16），为无阻尼响应，响应曲线为等幅振荡；

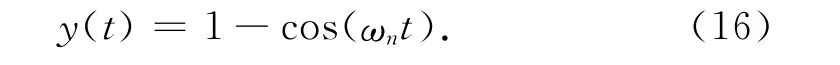
（2）当0＜ζ＜1时，则系统的响应表达式如式（17），为欠阻尼响应，响应曲线为衰减振荡；

（3）当ζ＝1时，则系统的响应表达式如式（18），为临界阻尼响应，响应曲线无振荡；

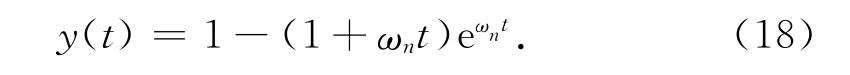
（4）当ζ＞1时，则系统的响应表达式如式（19），为过阻尼响应，响应曲线无振荡.

不同的阻尼比下的阶跃响应曲线可由MATLAB仿真得到，如图3所示.

图3 不同阻尼比下的二阶系统输出响应图

从仿真得到的曲线可以看出：ζ过大，调节时间长；ζ过小，系统会有较强振荡.为保证较短的调节时间和较小的超调量，可以从仿真曲线上得到最佳阻尼比约为ζ＝0.7，这一数值与理论值接近.

3 结论

笔者在控制理论教学（包括经典控制理论和状态空间理论）中引入MATLAB仿真，更新了传统控制理论课程中，对高阶系统难以求解特征根的陈旧观念，仿真曲线直观显示了控制系统的输出趋势，降低了教学难度，提高了教学效率；采用增广状态模型，解决了状态模型解析解中含有积分项的数值解的问题；以典型二阶系统为例进行仿真研究，较准确得到了典型控制系统的最佳参数结论，为控制理论的教育教学提供了有益参考.

［1]王万良.自动控制原理［M].北京：科学出版社，2011.

［2]王从庆，丁勇.现代控制理论课程教学改革的实践与探讨［J].南京航空航天大学学报：社会科学版，2004，6（1）：72-75.

［3]张利.自动控制理论课程的MATLAB辅助教学［J].电气电子教学学报，2003，25（1）：97-99.

［4]田思庆，吴桂云.自动控制原理课程的教学研究与实践［J].电气电子教学学报，2008，30（1）：112-114.

［5]刘琪，刘伟，张鸿辉，等.自动控制工程基础及应用［M].北京：航空工业出版社，2013.