Toeplitz方程组的拟对称化快速算法
2014-03-19王健,朱变,徐仲
王 健,朱 变,徐 仲
(1.周口师范学院 计算机科学与技术学院,河南 周口466001;2.西北工业大学 应用数学系,陕西 西安710072)
Toeplitz矩阵及Toeplitz方程组的求解在线性预测、数字信号处理、谱分析、误差控制码、控制论、系统识别及系统理论等领域内起着重要的作用[1-4].在求微分方程数值解和三次样条插值中常需求解以三对角Toeplitz矩阵为系数矩阵的线性方程组.1985年,Kumar将Toeplitz矩阵镶嵌成一个大的循环矩阵,进而得到求解Toeplitz方程组的快速算法[5].1986年,Ben-Artzi给出求非奇异Toeplitz矩阵逆的显示表达式,间接得到了求解Toeplitz方程组的快速算法[6].之后1986到1995年,Gohberg,Hsue等人相继给出了求Toeplitz方程组的快速算法[7,8].笔者通过构造特殊分块矩阵,间接得到了求解线性方程组Tx=b的解的快速算法,该算法所需计算量为O(n2).
1 算法推导
考虑求解Toeplitz线性方程组Tx=b,其中是n阶Toeplitz矩阵b=(b1,…,bn)T.容易验证Toeplitz矩阵T满足

构造2n阶方阵

如果求得线性方程组

的解向量y=(y1,y2,…,y2n)T,这里则y的前n个分量构成的列向量即是Toeplitz方程组Tx=b的解向量.利用式(1)易知式(2)的矩阵M满足
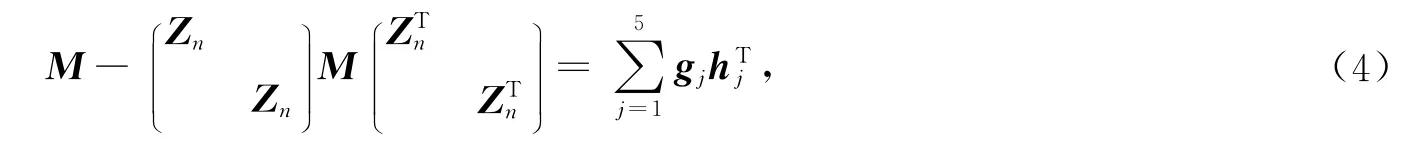
引理[4]设n阶矩阵A=(aij)n×n的顺序主子阵Ak(k=1,2,…,n)均可逆.给定线性方程组Ax=b,其中x=(x1,…,xn)T,b=(b1,…,bn)T.设bk=(b1,…,bk)T,又设线性方程组Akxk=bk和的解向量分别是xk=(xk1,…,xkk)T和uk=(uk1,…,ukk)T,其中e(k)k=(0,…,0,1)T,则
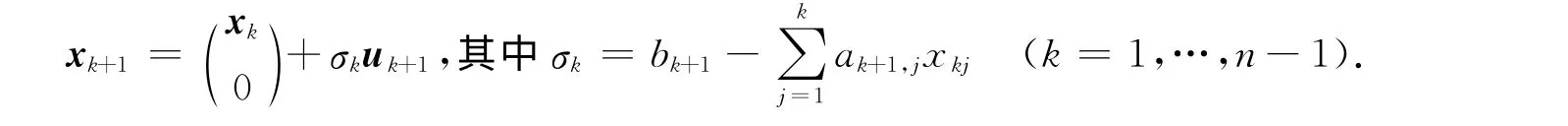
设式(2)的矩阵M的顺序主子阵Mk(k=1,…,2n)均是非奇异的分别是由gi,hi,f的前k个分量构成的列向量.又设yk=(yk1,…,ykk)T,uk=(uk1,…,ukk)T和…,5)分别是线性方程组的解向量.记

当k=n,…,2n-1时,由引理可得

而由式(4)得

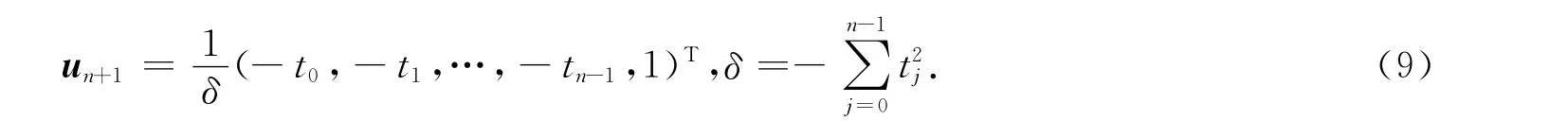
注意到Mn=In,所以故有
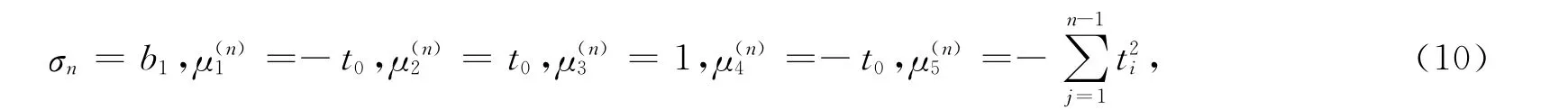
从而由式(6)和(7)即可求得yn+1和w(n+1)i(i=1,…,5).
当k=n+1,…,2n-1时,由式(4)得
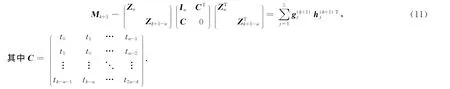
式(11)可变形为
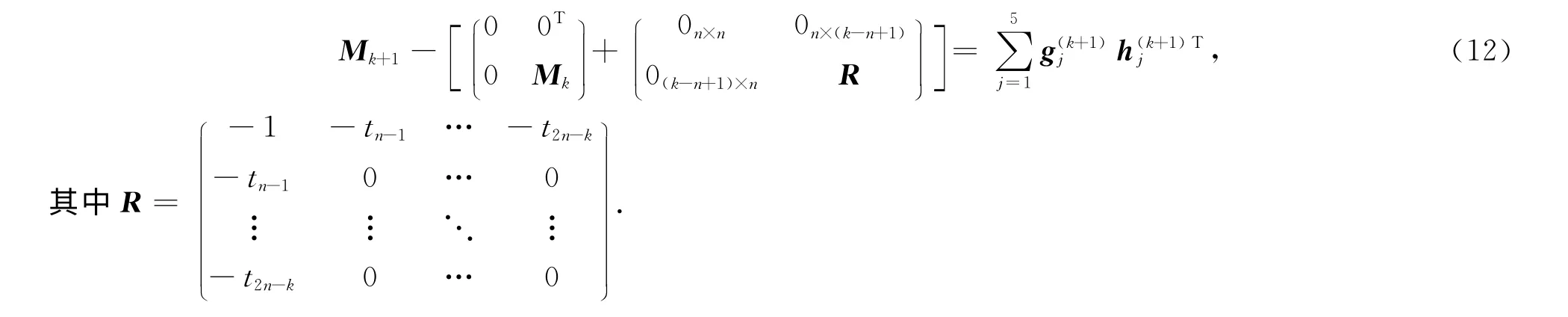

由引理得
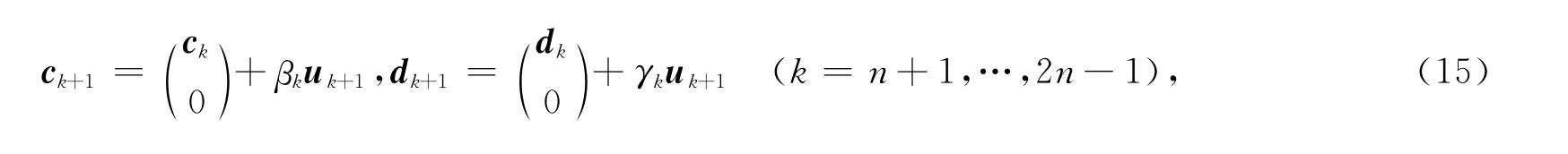
其中
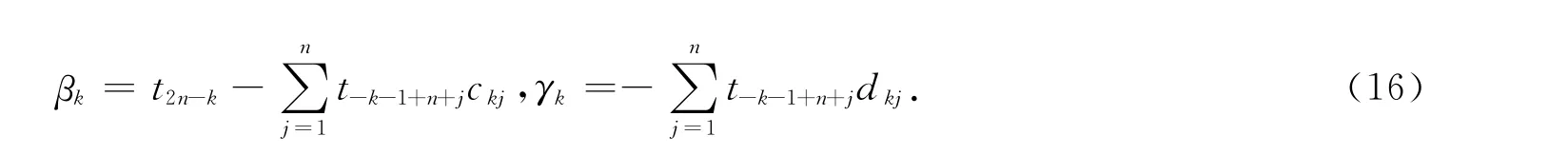
式(13)两边左乘M-1k+1得
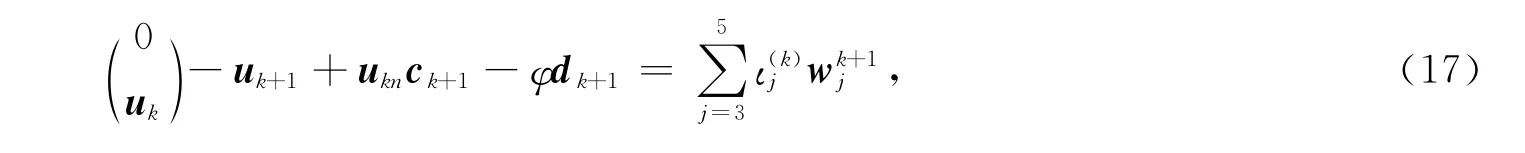
其中

把式(7)和式(15)代入式(17)整理得
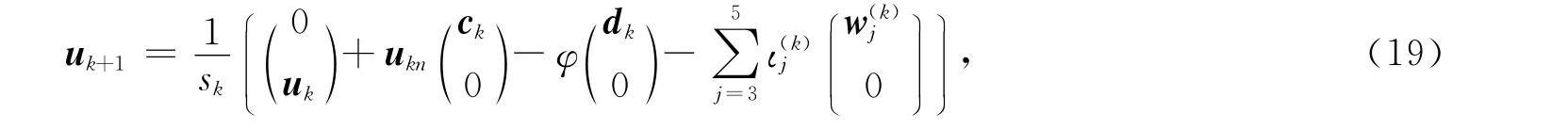
其中
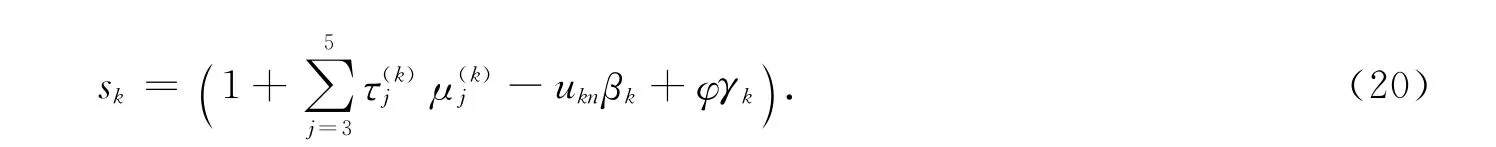
综上所述即得求解Toeplize方程组Tx=b的如下算法.

2 数值算例
笔者找了一些Toeplitz矩阵在微机PⅣ(CPU 2.00GHz,内存256MB)上用Matlab语言编程求解Toeplitz方程组Tx=b,分别利用本文给出的快速算法、Zohar算法和Gohberg-Kailath-Koltracht算法(简记为GKK算法)进行计算,误差用‖Tx-b‖2度量,时间为秒.算例如下:
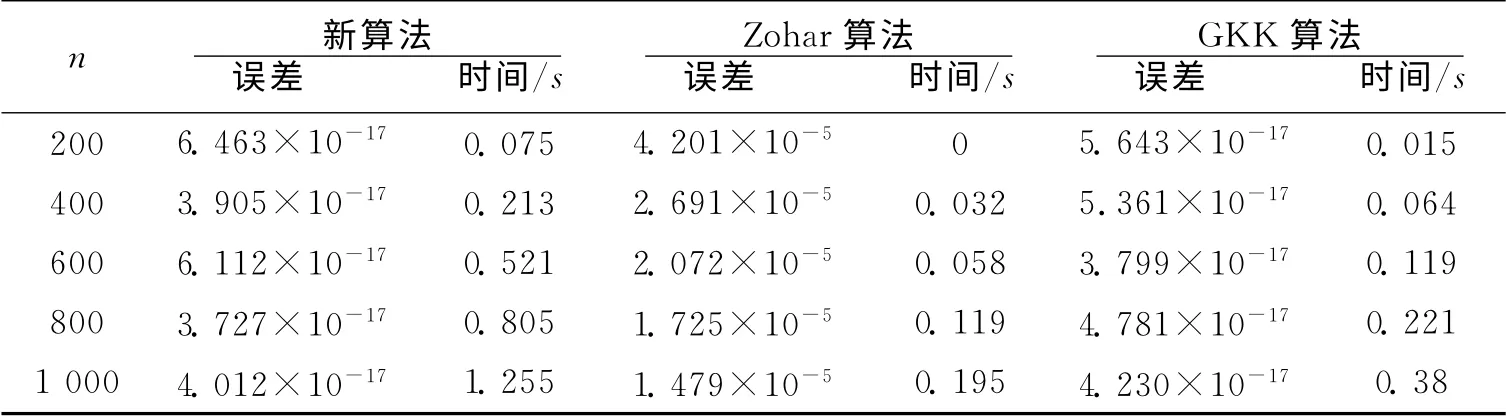
表1 三种算法计算误差及其计算时间比较
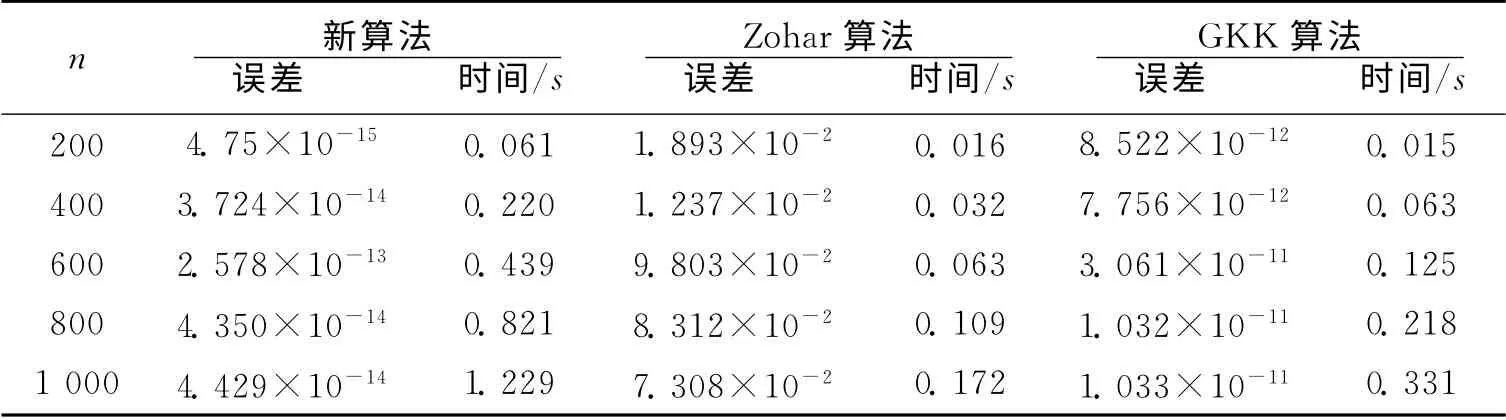
表2 三种算法计算误差及其计算时间比较
算例表明,用笔者所得的快速算法求Toeplitz线性方程组的解,其计算精度比Zohar算法的精度高很多,和Gohberg-Kailath-Koltracht算法的精度各有所长;而所需的时间比Zohar算法和Gohberg-Kailath-Koltracht算法多.
[1]Ulrych T J,Smylie D E,Jensen O G,et al.Predictive filtering and smoothing of short records by using maximum entropy[J].J.Geophys.Res.,1973,78:4959-4964.
[2]Morf M.Fast algorithms for multivariable systems[D].Stanford,CA,1974.
[3]Makhoul J.Linear prediction:a tutorial review[J].Proc.IEEE,1975,63:561-580.
[4]徐仲,张凯院,陆全.Toeplitz矩阵类的快速算法[M].西安:西北工业大学出版社,1998:5-6.
[5]Kumar R.A fast algorithm for solving a Toeplitz system of equations[J].IEEE ASSP,1985,33:254-267.
[6]Ben-Artzi A,Shalom T.On inversion of Toeplitz and close to Toeplitz matrices[J].Linear Algebra Appl.,1986,75:173-192.
[7]Gohberg I,Kailath T,Koltracht I.Efficient solution of linear systems of equations with recursive structure[J].Linear Algebra Appl.,1986,80:81-113.
[8]Jin-Jen Hsue,Andrew E,Yagle.Fast algorithms for solving Toeplitz systems of equations using number-theoretic transforms[J].Signal Processing,1995,44:89-101.
[9]安晓红,徐仲,叶正麟.Toeplitz方程组极小范数最小二乘解的快速算法[J].数学的实践与认识,2008,38:40-46.
