AlSb(110)基外延生长Bi薄膜的第一性原理研究
2014-03-19文黎巍
丁 俊,文黎巍
(河南工程学院 理学院,河南 郑州451191)
由于半金属Bi的一系列特殊的性质,如比较高的电子迁移率,电子和空穴的低费米能级,有效电子质量较小等[1],被认为是一种合适的材料在理论和实验上对其量子尺寸效应进行研究.过去的20年中,Bi薄膜在半导体衬底,特别是III-V(110)族元素组成的衬底表面生长方面在理论和实验中都得到了广泛的研究[2-7].在这些体系里,由于衬底和薄膜交界面处不发生化学反应,在一定的条件下,衬底上的金属原子可以生长成为大的平台或岛状结构.这些平台和岛具有平坦的顶部和陡峭的边缘,并且只能具有特定的厚度.这种不同寻常的行为第一次是在Ag/GaAs[8]体系中发现,随后又在其他 体 系 中 发 现,比 如Ag/Si(111)[9]和Pb/Si(111)体系[10,11].张振宇等[12]用“电荷生长”模型成功地解释了这种现象,并提出了平坦薄膜生长的条件以及纳米结构的条件.
虽然Bi薄膜和III-V(110)族元素衬底之间的作用已有研究,但是Bi和AlSb之间的作用还未报道.笔者用基于密度泛函理论(DFT)框架下的Vienna ab-initio Simulation Package(VASP)程序计算,对AlSb(110)衬底外延生长Bi薄膜的特性进行研究.分别计算了外延生长1~6层Bi薄膜的能带和带隙大小,发现了不同层数传导特性的奇偶振荡转变.分析了其成因并总结其振荡规律.
1 计算方法
计算采用的是基于密度泛函理论平面波赝势方法的VASP程序[13,14],用局域密度近似(LDA)处理交换关联作用.笔者采用的是周期性平板模型,每一平板包括8层AlSb衬底,两侧分别有一定层数的Bi薄膜.最上面几层Bi原子采用的是外延生长结构模型,也就是Bi原子以锯齿链的形式在[1ī0]方向外延生长,相当于在AlSb(110)衬底上生长[15].为优化原子结构,对衬底和衬底上的原子进行弛豫,力的收敛标准为0.02eV/Å.布里渊区K点数选为9×9×1形式.Bi薄膜最厚为6层时相应的真空层厚度为20Å,以减少周期性边界条件的影响.
2 结果与讨论
AlSb为闪锌矿结构,实验上测得晶格常数为0.614nm,LDA进行结构优化,晶格常数为0.611 nm时能量最低.晶体Bi为斜方形结构,其实验晶格常数为0.472nm,理论优化晶格常数为0.467 nm.LDA计算结果均小于实验值,与LDA近似通常低估晶格常数一致.III-V族元素半导体(110)表面的特殊之处在于其表面原子形成之字形链状结构,而Bi和Sb原子在其表面并不破坏沉底结构,也不会形成团簇,而是会和衬底一一对应形成外延连续层结构[2-5].
图1(a)~(f)分别给出了AlSb(110)衬底表面外延生长1~6层Bi薄膜的能带结构.从图1(a)中可以看到外延生长1层Bi薄膜的主体带隙间有4条子能带,其中能量低的两条为满带,高的两条为空带.此体系显示出非金属性,并计算出带隙为0.5eV.图1(b)中看出外延生长2层Bi薄膜的主体带隙间增加了2条子能带,且交叠横穿费米能级,显示出金属性.有趣的是,这些横穿费米能级的子能带随着Bi薄膜厚度的增加振荡出现,在3层消失而在4层又出现.3层Bi薄膜显示出非金属性,其带隙为0.1eV,4层和5层以上都显示出金属性,如图1所示.
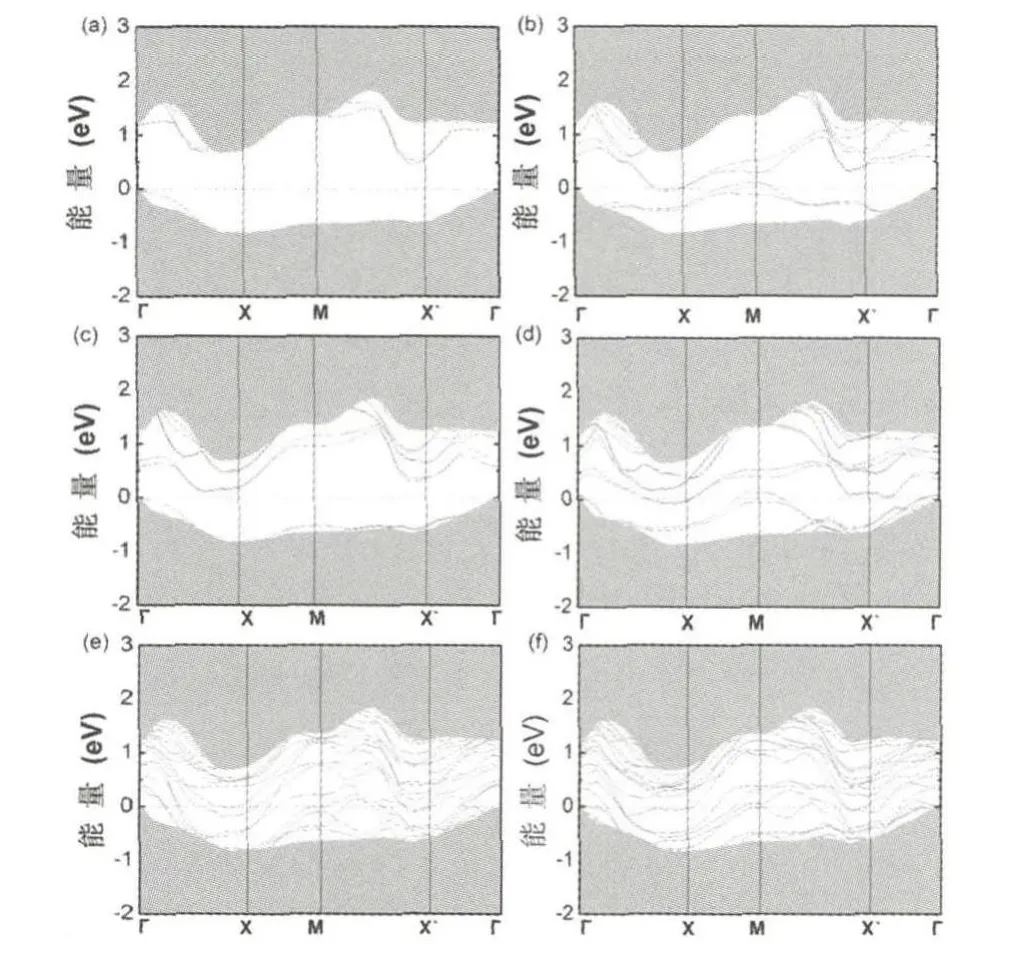
图1 AlSb(110)衬底表面外延生长1-6层Bi薄膜的能带图
笔者采用局域密度近似(LDA)交换关联能函数对带隙进行计算,图2给出了不同层Bi薄膜的带隙计算结果.由于LDA计算比实际值要低,因此外延生长3层Bi薄膜的带隙要大于0.1eV.由于外延生长2层和4层Bi薄膜的费米能级处有2条子能带穿越,显示出金属性,因此与1层和3层的Bi薄膜相比,它们相对不稳定.
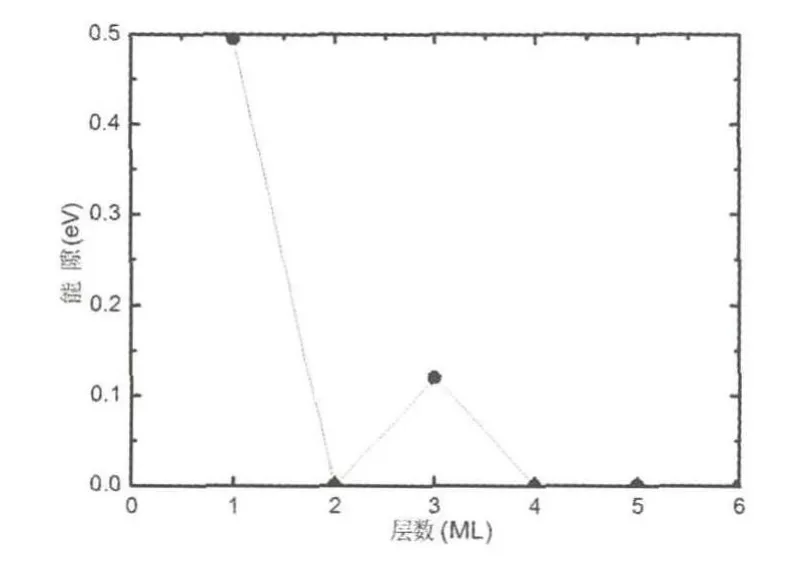
图2 Bi/AlSb(110)体系层数与带隙关系图
显而易见,在AlSb(110)衬底表面外延生长的Bi薄膜显示出非金属-金属的奇偶振荡转变.在很长一段时间,由于Bi的独特性质,人们都期望Bi薄膜产生非金属-金属的转变.许多输运和光学测量实验都指出了非金属-金属的转变与Bi薄膜的厚度有关,存在奇偶振荡.但到目前为止,还没有人给出明确的结论[16,17].基于此,笔者用第一性原理计算给出了结果.这种非同寻常的非金属-金属的奇偶振荡转变可以这样理解:因为与衬底接触的第1层Bi原子与衬底作用较强,笔者认为量子阱从第2层开始.从第2层开始,每个Bi原子的配位数是4,然而一个Bi原子具有6个价电子,因此外延生长的每个Bi原子具有两个自由电子.对于1×1的单元晶胞,每一层有一个Bi原子,对应两个自由电子,所以总共的自由电子数目为2n,n=1,2,3,…,对应层数为2,3,4,….从另一方面说,每增加一层,就出现两个子能带,不同层数的Bi原子对应形成不同的子能带.当薄膜厚度非常薄,只有几个原子层时,不同层的原子形成的子能带不存在相互交叠,依据Wilson法则[18]可以出现金属-非金属的转变:偶数层是金属,奇数层是非金属.因此2,4层为金属,3层为非金属.当薄膜超过临界厚度时,不同层数原子形成的子能带相互交叠,振荡消失,只显示金属性.从图1可以看出,笔者的计算结果非常符合这一法则.这是由于自由电子在薄膜中受到二维势阱作用,不同层厚对应不同的量子势阱而表现出来的量子尺寸效应.
3 结论
用第一性原理密度泛函理论研究了在AlSb(110)衬底上外延生长不同层Bi薄膜体系的能带结构和能隙大小.结果发现,外延生长1层和3层Bi薄膜时显示出非金属性,而生长2层和4层及5层以上时显示出金属性,形成金属-非金属传导特性的奇偶振荡,这是由薄膜的量子尺寸效应引起的.
[1]Hofmann P.The surfaces of bismuth:Structural and electronic properties[J].Prog Surf Sci,2006,81(5):191.
[2]Gay S C A,Çakmak M,Srivastava G P.Comparative study of Bi overlayers on III-Sb(110($1\times 1$)surfaces[J].Surf Sci,2000,454:26-29.
[3]Schmidt W G,Bechstedt F,Srivastava G P.Adsorption of group-V elements on III-V(110)surfaces[J].Surf Sci Rep,1996,25:141-223.
[4]Umerski A,Srivastava G P.Geometry and electronic band structure of an ordered monolayer deposition of Bi on III-V(110)semiconductor surfaces[J].Phys Rev B,1995,51:2334.
[5]Dura J A,Vigliante A,Golding T D,et al.Epitaxial growth of Sb/GaSb structures:An example of V/III-V heteroepitaxy[J].J Appl Phys,1995,77:21-27.
[6]McIlroy D N,Heskett D,Swanston D M,et al.Occupied surface-state bands of Bi(1×1)overlayers on an InAs(110)surface grown by molecular-beam epitaxy[J].Phys Rev B,1993,47:3751.
[7]Patrin J C,Li Y Z,Chander M,et al.Sb and Bi on GaAs(110):Substrate-stabilized overlayer structures studied with scanning tunneling microscopy[J].Phys Rev B,1992,46:10221.
[8]Smith A R,Chao K,Niu Q,et al.Formation of Atomically Flat Silver Films on GaAs with a“Silver Mean”Quasi Periodicity[J].Science,1996,273(5272):226-228.
[9]Gavioli L,Kimberlin K R,Tringides M C,et al.Quantum Growth of Ag Islands on Si(111):Plateous with a Magic Height[J].Phys Rev Lett,1999,82:129.
[10]Budde K,Abram E,Yeh V,et al.Uniform,self-organized,seven-step height Pb/Si(111)-(7×7)islands at low temperatures[J].Phys Rev B,2000,61:R10602.
[11]Yeh V,Berbil-Bautista L,Wang C Z,et al.Role of the Metal/Semiconductor Interface in Quantum Size Effects:Pb/Si(111)[J].Phys Rev Lett,2000,85:5158.
[12]Zhang Z,Niu Q,Shih C.“Electronic Growth”of Metallic Overlayers on Semiconductor Substrates[J].Phys Rev Lett,1998,80:5381.
[13]Kresse G,Furthmller J.Efficient iterative schemes for ab initio total-energy calculations using aplane-wave basis set[J].Phys Rev B,1996,54:11169.
[14]Vanderbilt D.Soft self-consistent pseudopotentials in ageneralized eigenvalue formalism[J].Phys Rev B,1990,41:7892.
[15]Cho J,Niu Q,Zhang Z.Oscillatory nonmetal-metal transitions of ultrathin Sb overlayers on a GaAs(110)substrate[J].Phys Rev Lett,1998,80:3582.
[16]Hoffman C A,Meyer J R,Bartoli F J,et al.Semimetal-to-semiconductor transition in bismuth thin films[J].Phys Rev B,1993,48:11431.
[17]Garcia N,Kao Y H,Strongin M.Galvanomagnetic Studies of Bismuth Films in the Quantum-Size-Effect Region[J].Phys Rev B,1972,5:20-29.
[18]Wilson A H.Proceedings of the Royal Society of London[J].Series A,1931,133:458-491.
