含摩擦滑移铰及驱动约束多刚体系统数值算法*

王晓军 王琪 庄方方

(1.常州工学院机电学院，常州 213002)(2.北京航空航天大学航空科学与工程学院，北京 100191)

引言

非光滑多体系统动力学是在光滑多体系统动力学研究的基础上逐步发展起来的新的研究领域，主要研究非光滑因素(如摩擦与碰撞)对多体系统动力学行为的影响.如步行机器人在地面上行走、航天器的空中对接、机械手抓取工件和具有非理想约束铰链(考虑间隙与摩擦的滑移铰和转动铰)的机械系统等都存在物体间的接触与分离、滑移与粘滞等现象(称为非光滑事件).由于这些非光滑事件的存在，导致系统的动力学方程不连续或分段连续，给非光滑事件的判断和动力学方程的求解带来了新的困难.

上个世纪末，Pfeiffer研究了具有单边约束非光滑多体系统动力学［1］，通过引入互补概念，有效地解决了非光滑事件的判断;随着研究的不断深入，逐步形成了事件驱动法和时间步进法［2］.段文杰应用非光滑动力学的时间步进法研究了被动行走器足地间的库伦摩擦系数和碰撞恢复系数对被动行走器动力学行为的影响［3］.Flores研究了具有非理想铰链多体系统的运动学与动力学问题［4］，研究了铰链的间隙、摩擦和润滑剂等因素对多体系统动力学行为的影响，数值结果表明，随着间隙的减小，由于接触碰撞引起的法向约束力的突变也随之减小，然而当采用时间步进法研究含非光滑铰链多体系统动力学时，随着间隙的减小，违约问题将逐步凸显［5］.文献［6］用非光滑多体系统动力学方法研究了滑移铰含摩擦多体系统的建模与数值计算方法，当滑移铰的间隙充分小时，将机械系统中滑移铰的滑块视为质点，滑块与滑道间的几何约束视为定常的双边约束，建立了双边约束法向力的互补关系，应用水平线性互补［7］和事件驱动法给出了非光滑事件判断的计算方法，应用Baumgarte约束稳定化方法［8］在一定程度上解决了约束的违约问题.若能将文献［6］的方法推广到非定常约束(如驱动约束)的多体系统，且滑移铰的滑道不是固定的而是运动的(如曲柄摇杆机构中的摇杆)，则可使非光滑多体系统动力学方法的应用领域更加广泛.

本文将研究具有非定常约束(驱动约束)及滑移铰含摩擦的非光滑多体系统动力学的建模方法与数值计算方法，应用库仑干摩擦模型作为滑移铰间的摩擦模型，应用线性互补方法建立滑移铰法向约束力的互补关系，将约束分为几何的定常约束(滑移铰约束)和非定常约束(驱动约束)，应用具有约束稳定化的增广法和事件驱动法建立该系统的动力学方程，最后通过算例说明本文给出方法的有效性.

1 非光滑滑移铰力学模型

1.1 滑移铰几何约束模型

滑移铰是机械系统中常见的运动副.在有些机构中，当间隙充分小时，滑移铰被视为双边约束且其中的滑块被视为质点［6］，此时滑移铰的力学模型如图1所示，其中是滑道两侧分别作用在滑块上的法向约束力.设系统中的第i个滑移铰的约束方程为

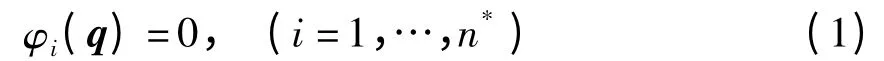
式中，q=［q1，…，qk］为系统的广义坐标，n*为滑移铰的个数.若用递推法［9］或用距离函数列写滑移铰的约束方程，则约束方程(1)对应的Lagrange乘子为滑道作用在滑块i上的法向约束力.

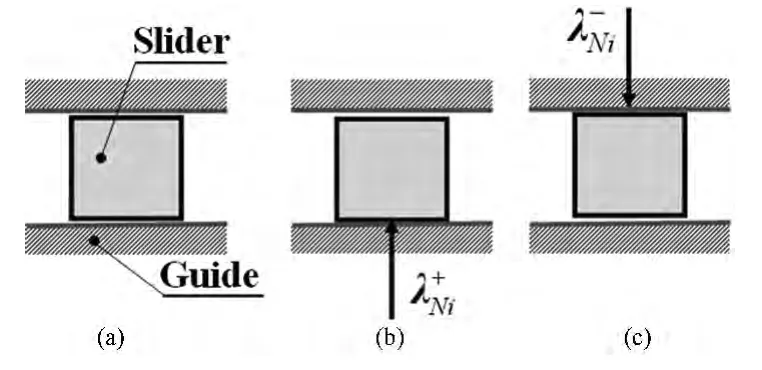
图1 滑移铰模型Fig.1 The model of translational joints

当λNi=0时，滑道与滑块无接触，如图1(a)所示;当λNi＞0时，滑道的一侧与滑块接触，如图1(b)所示;当λNi＜0时，滑道的另一侧与滑块接触，如图1(c)所示.滑道作用于滑块上的两个法向约束力，与Lagrange乘子λNi具有下列关系［6］

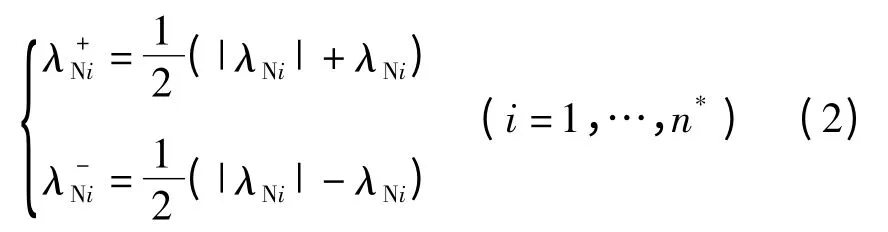
且满足下列互补条件

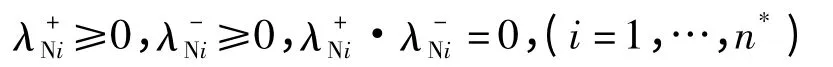
设

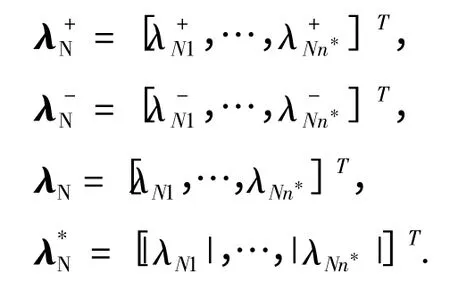
则由式(2)可得

1.2 滑移铰摩擦模型

机械系统中常用的摩擦模型有多种［10］，其中库仑摩擦模型又可分为库仑干摩擦模型和修正的库仑摩擦模型［4］，前者是相对速度的非连续函数(给数值计算带来一定的困难)，后者是相对速度的连续函数(不易反映库仑摩擦的静动态特性)［6］.本文将采用库仑干摩擦模型作为滑移铰的摩擦模型.

应用非光滑动力学方法，库仑干摩擦模型可表示为

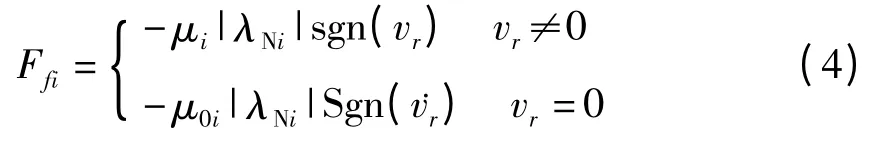
式中，Ffi为滑道作用在滑块上的摩擦力在切向上的投影;μi，μ0i分别为滑道与滑块间的动、静摩擦因数;|λNi|为作用于滑块上法向约束力的大小;Sgn()为符号函数;vri，˙vri分别为滑块相对滑道的相对速度和相对切向加速度;Sgn()为集值函数［11，12］，可表示为

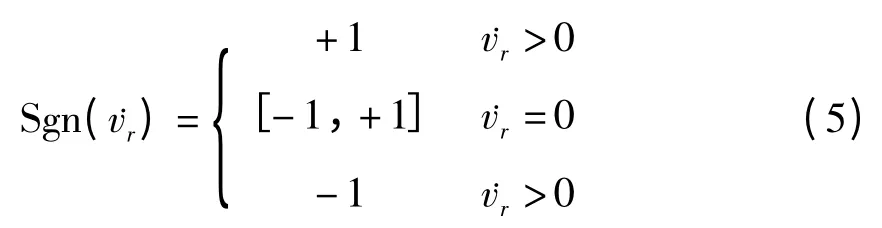
由式(4)和式(5)，可以看出，当滑块的相对速度和相对切向加速度均为零时，摩擦力的取值是一个范围，即当滑道内的滑块处于粘滞状态时，摩擦力的取值在该范围内.

2 非光滑动力学方程

2.1 多体系统动力学方程

第一类Lagrange方程是建立多体系统动力学方程的有效方法之一.设滑移铰的约束方程由方程(1)表示，将其用向量形式表示为

式中，Φ=［φ1，…，φn*］T.设系统的驱动约束方程为

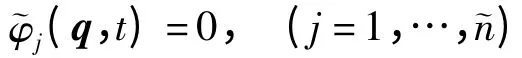
则由第一类Lagrange方程可得到系统的动力学方程为

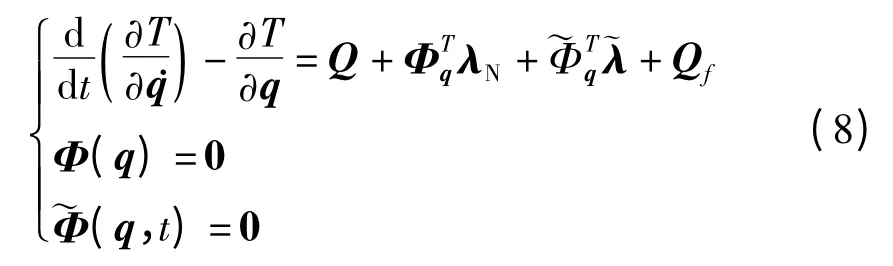
式中，P中各元素为系统广义坐标及其对时间一阶和二阶导数的函数=［|λN1|，…，|λNn*|］T.

将式(9)代入式(8)，并应用Baumgarte约束稳定化方法，方程(8)可表示为

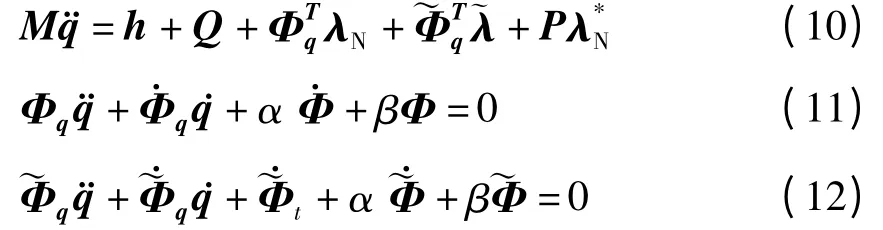
式中，

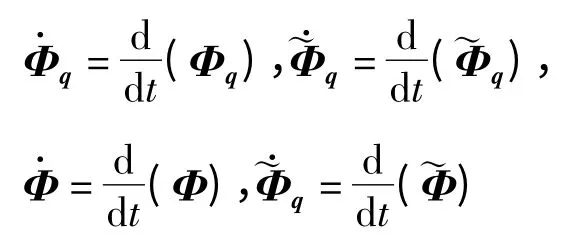
方程(10)～(12)为具有约束稳定化的动力学方程.当系统是光滑时，P=0，方程组(10)～(12)是关于，λN的线性代数方程组，可用相关的数值计算方法求解，但是对于非光滑系统，P≠0中含有|λNi|(i=1，…，n*)，则该方程组不是关于，λN的线性代数方程组，不能用线性代数方程组的数值计算方法求解.

2.2 线性互补算法

利用式(3)，可将方程组(10)～(12)表示成线性互补方程.为便于推导，将方程(10)～(12)表示成

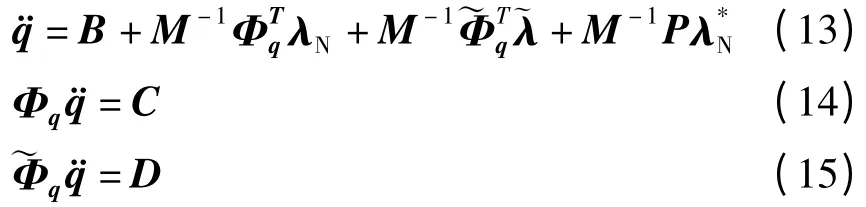
式中，

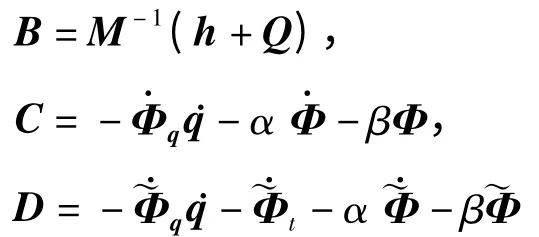
将(13)式代入(15)式，可求得

式中，

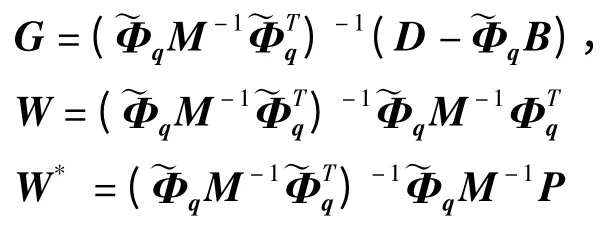
将式(16)代入(13)得

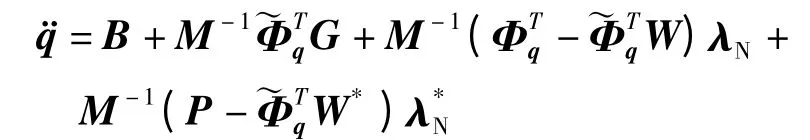
将上式代入式(14)得

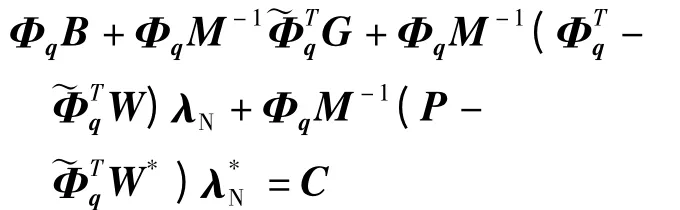
再将上式表示为

式中，

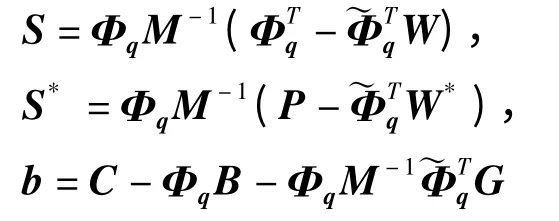
将式(3)代入式(17)可得

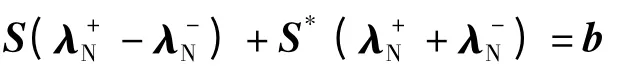
将上式表示成

且

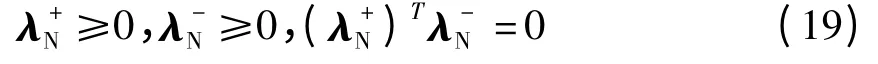
式中，

式(18)和式(19)为标准的水平线性互补问题(HLCP)［6］，应用线性互补的计算方法可求出，;然后将其代入式(3)可得到λN，;再将其代入式(16)，则可求出驱动约束力(或力偶)~λ.将相关的约束力代入方程(10)，应用常微分方程的数值计算方法即可求出该系统的运动特性.

3 算例

3.1 力学模型

本文以曲柄摇杆机构为例，如图2所示，其中摇杆OA和曲柄O1B均视为刚体，滑块B视为质点.

该系统参数分别为:摇杆对O轴的转动惯量为J1=16/3kg·m2，质量为m1=4.0kg，其质心到O轴的距离为L1=1.0m;曲柄对O1轴的转动惯量为J2=1/6kg·m2，质量为m2=2.0kg，其质心到O1轴的距离为L2=0.25m;滑块的质量为m3=0.5kg，到O1轴的距离为L3=0.5m;O轴到O1轴的距离为L4=1.0m;滑块与滑道间的动滑动摩擦因数为μ=0.2;曲柄的角速度ω=3.0rad/s.

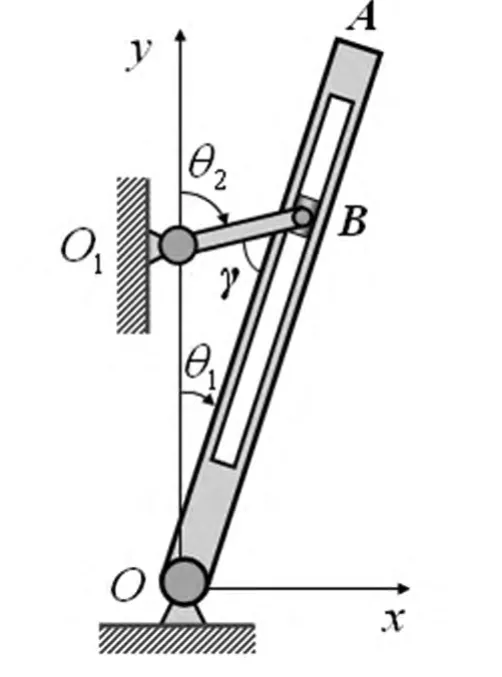
图2 曲柄-摇杆机构Fig.2 Crank-rocker mechanism

系统的广义坐标为q=［θ1，θ2］T，分别为摇杆和曲柄与铅垂轴y的夹角;γ=θ2-θ1为摇杆与曲柄间的夹角.设滑移铰B的约束方程和曲柄的驱动约束方程分别为

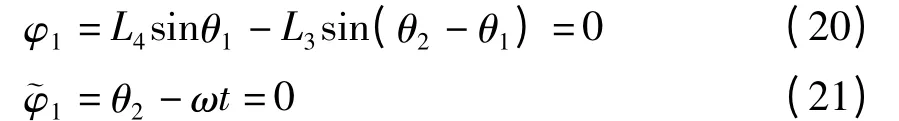
由于该系统在运动过程中，滑块相对摇杆无相对静止状态(当滑块的相对速度为零时，其相对加速度不为零)，因此滑块相对滑道无粘滞状态，则摩擦力的广义力可表示为

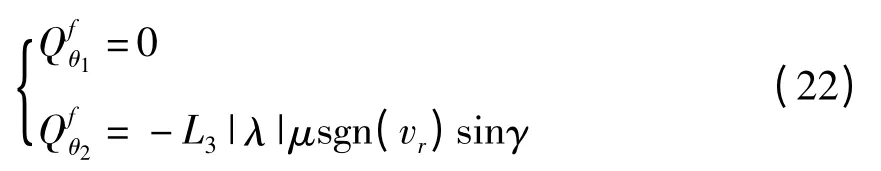
式中，vr为滑块相对摇杆的相对速度.

设摇杆在运动过程中受到线性阻力矩的作用(Mf=-c)，其中为阻尼系数.当约束方程约束的是线位移时，对应的Lagrange乘子是约束力，当约束方程约束的是角位移时，对应的Lagrange乘子为约束力偶矩.

3.2 数值分析

根据约束方程(20)和驱动约束方程(21)可知，曲柄匀角速度转动，摇杆往复摆动.应用本文给出的计算方法对该系统进行数值仿真，图3给出了摇杆的角速度(实线)和曲柄的角速度(虚线)的时间历程.图4给出了摇杆的角加速度与曲柄转角θ2的对应关系，从图中可以看出，当θ2=0rad或θ2=πrad时，摇杆的角加速度为零(这与定性分析的结果相吻合).

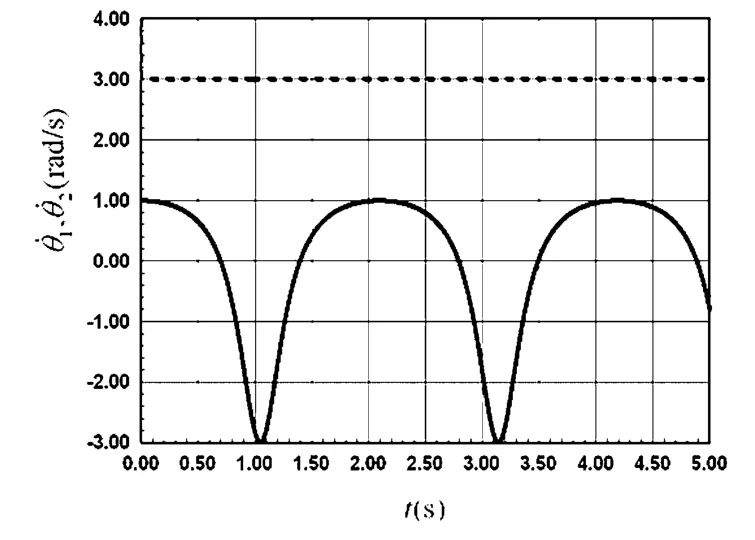
图3 和的时间历程图Fig.3 The time history of and

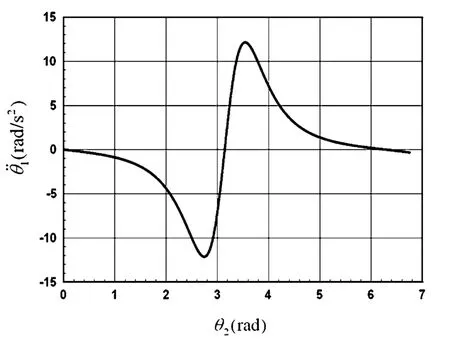
图4 摇杆OA的角加速度图Fig.4 Angular acceleration of rocker OA

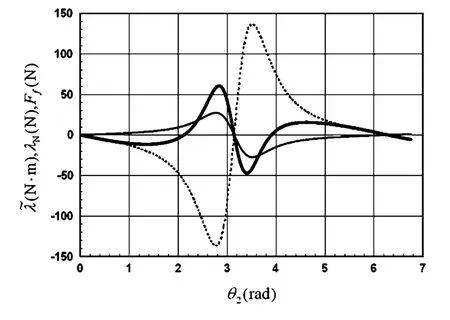
图5 λN和Ff图(无阻尼)Fig.5 λN and Ff with c=0

图6给出了当摇杆的阻尼系数不为零时(即:c=8.0N·m·s/rad)，作用于滑块上的摩擦力Ff与广义坐标θ2的对应关系.当θ2=0rad或θ2=πrad时，有θ1=0°=0.0rad/s2，λN≠0且滑块相对速度的方向发生改变，导致Ff的值发生突变.

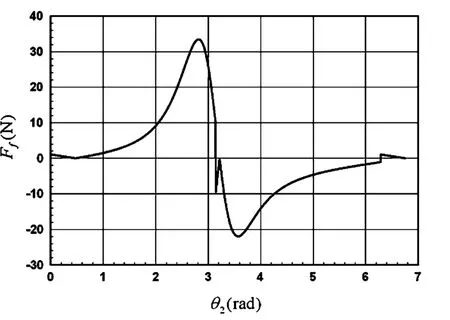
图6 Ff～θ2(c=8.0N·m·s/rad)Fig.6 Ff～θ2(c=8.0N·m·s/rad)

上述仿真结果与用牛顿-欧拉方法建立的动力学方程求得的数值结果完全吻合.

在本算例中，若α＞1.0，β＞1.0，在数值计算时，设计算步长为h，当计算步长满足0＜h≤0.001时，约束方程满足若α=0，β=0，h=0.001，约束方程不能被满足，其计算结果发散.

4 结论

本文研究了非光滑滑移铰平面多刚体系统驱动力的数值计算方法.应用第一类Lagrange方程建立了该系统的动力学方程，将滑移铰视为双边约束，分别建立驱动约束方程和滑移铰的运动约束方程，与驱动约束方程对应的Lagrange乘子为驱动力或驱动力偶矩，与滑移铰的运动约束方程对应的Lagrange乘子为作用在滑移铰的法向约束力;滑移铰的摩擦模型采用库仑摩擦模型，为便于计算摩擦力的广义力，建立了滑移铰法向约束力的互补关系，将其法向约束力的计算转化为线性互补方程的求解;结合Baumgarte约束稳定化方法和常微分数值计算方法，给出了该系统驱动力及系统动力学响应的数值计算方法.最后以曲柄-摇杆机构为例，通过数值仿真说明了本文给出方法的有效性.

1 Pfeiffer F，Glocker C.Multibody dynamics with unilateral contacts.New York:John Wiley＆Sons.Inc.，1996

2 Pfeiffer F，Foerg M，Ulbrich H.Numerical aspects of nonsmooth multibody dynamics.Computer Methods in Applied Mechanics and Engineering，2006，195:6891～6908

3 段文杰，王琪，王天舒.圆弧足被动行走器非光滑动力学仿真研究.力学学报，2011，43(4):765～774(Duan W J，Wang Q，Wang T S.Simulation research of a passive dynamic walker with round feet based on non-smooth method.Chinese Journal of Theoretical and Applied Mechanics，2011，43(4):765～774(in Chinese))

4 Flores P，Ambrosio J，Pimenta Claro J C，et al.Kinematics and dynamics of multibody systems with imperfect joints.Berlin:Springer-Verlag，2008

5 Flores P，Leine R，Glocker C.Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach.Multibody System Dynamics，2010，23:165～190

6 Wang Q，Peng H L，Zhuang F F.A constraint-stabilized method for multibody dynamics with friction-affected translational joints based on HLCP.Discrete and Continuous Dynamical Systems Series B，2011，16(2):589～605

7 韩继业，修乃华，戚厚铎.非线性互补理论与算法.上海:上海科学出版社，2006(Han JY，Xiu N H，Qi H D.Theory and algorithm of nolinear complementarity.Shanghai:Shanghai Scientific＆Technical Publishers，2006(in Chinese))

8 Flores P，Machado M，Seabra E，Silva M T.A parametric study on the Baumgarte stabilization method for forward dynamics of constrained multibody systems.ASME Journal of Computational and Nonlinear Dynamics，2011，6:011019

9 洪嘉振.计算多体系统动力学.北京:高等教育出版社，2001(Hong J Z.Calculation of dynamics of multibody system.Beijing:Higher Education Press，2006(in Chinese))

10 刘丽兰，刘宏昭，吴子英等.机械系统中摩擦模型的研究进展.力学进展，2008，38(2):200～213(Liu L L，Liu H Z，Wu Z Y，et al.An overview of friction models in mechanical systems.Advances in Mechanics，2008，38(2):200～213(in Chinese))

11 Zhuang F F，Wang Q.Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints.Multibody System Dynamics，2013，29:403～423

12 Acary Vincent，Brogliato Bernard.Numerical methods for nonsmooth dynamical systems.Berlin:Springer-Verlag，2008