一类非线性切换系统鲁棒H∞可靠控制*

卢军锋 吴钟鸣 向峥嵘

(1.金陵科技学院学院机电工程学院，南京 211169)(2.南京理工大学自动化学院，南京 210094)

引言

切换系统是一类十分重要的混杂系统，一般情况下系统包含一个切换规则和由多个微分方程所构成的子系统，该系统有着重要的理论价值与广泛的工程背景，切换系统的研究可以为许多领域提供理论支持，目前已经受到越来越多关注［1-4］.

控制系统在实际工作中，来自内部与外部的干扰是很多的，比如传感器测量误差，温度引起的参数变化等，会给系统带来很多的不确定性，因此系统带有参数不确定性是普遍存在的情况.另外，系统中的执行器的故障是不可避免的，它的故障会导致系统不能正常工作从而带来十分严重的后果.因此，带有参数不确定性和外部扰动的切换系统的可靠控制研究是十分必要的［5-9］.文献［6］研究了一类线性切换系统的鲁棒可靠控制问题，运用凸组合技术设计可靠状态反馈控制器，使得闭环系统是渐进稳定的;文献［7］运用时间驻留法对线性切换系统鲁棒容错控制进行了研究，设计状态反馈控制器;文献［8］研究了一类含有非线性干扰的时滞切换系统鲁棒容错控制问题，使得系统全局渐近稳定.上述这些文章稳定的前提是控制器在确定的切换规则下切换，因此不能满足任意切换规则的要求，另外，这些文章在研究可靠控制时，对系统抑制外界扰动的H∞性能指标和所有系统矩阵都含不确定项的情况没有充分考虑.然而，在实际系统中这些问题是广泛存在的，而且是十分重要的.

本文利用LMI方法和公共利亚普诺夫函数方法，将可靠控制技术与切换控制技术相结合，给出系统存在扰动以及不确定性时，在任意切换规则下的鲁棒反馈可靠控制器存在的充分条件，以保证系统在执行器正常和失效时仍能使系统全局二次稳定，并且满足一定的扰动抑制性能指标.

1 问题的描述与准备知识

考虑以下的非线性不确定切换系统:

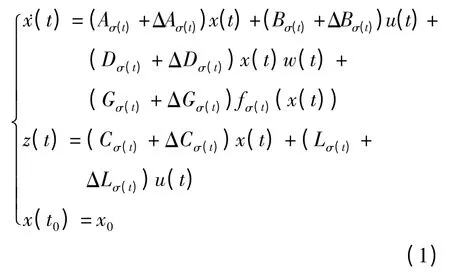
其中，x(t)∈Rn为系统状态向量，u(t)∈Rk为系统的输入信号，w(t)∈Rp是属于L2∈［0，∞)的噪声，z(t)∈Rq为被控输出向量，fσ(t)(x(t))为系统的非线性函数，σ(t):R+→M={1，2，…，m}为系统的切换信号，它是一个依赖于状态或时间的分段常值函数，对于Ai，Bi，Ci，Di，Gi，Li为已知实常数矩阵，并且

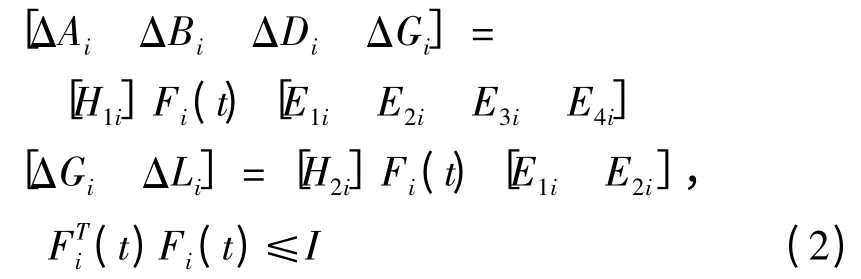
其中H1i，H2i，E1i，E2i，E3i，E4i为已知适维实常矩阵.假设1:对于任意的i∈M，非线性部分fi满足全局Lipschitz条件

其中Mi为已知的Lipschitz常数矩阵.定义1:给定扰动性能指标γ＞0，系统参数不确定性满足式(2)，那么在任意随机切换规则以及执行器失效的情况下，设计反馈控制器，使得系统(1)当w=0时闭环系统是二次稳定的，且在x(t)=0时，控制输出z满足‖z‖2＜γ‖ω‖2，∀ω(t)∈L2∈［0，∞)则称控制器是系统(1)的鲁棒H∞次优可靠控制器，若该控制器使得γ最小，则该控制器为系统(1)的鲁棒H∞最优可靠控制器.

引理1 X，Y为任意适当维数的矩阵，若常数ξ＞0，则如下不等式成立

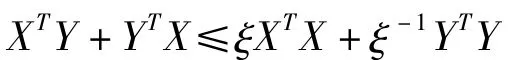
引理2 矩阵ΔBi=H1iFi(t)E2i，其中Hi1，E2i为已知适维实常矩阵，且(t)Fi(t)≤I.如果有常数ρi，i={1，…，m}，使得ρiI-E2i＞0，则下列不等式成立

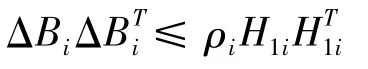
证明:定义

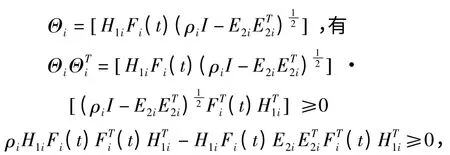
那么ΔBiΔ≤ρiH1i.

引理3 Y，D，E是任意适当维数的矩阵，其中Y是对称的，Y+DF(t)E+ETFT(t)DT≤0对所有满足FT(t)F(t)＜I的矩阵F(t)成立，当且仅当存在常数ε＞0，使得，Y+εDDT+ε-1ETE≤0.

在研究可靠控制问题时，将切换系统(1)的执行器分成两部分，第一部分结构形式为Ωi⊆{1，2，…，n}(i∈M)，表示系统运行时可能失效的全体执行器所组成的集合;第二部分为⊆{1，2，…，n}-Ωi(i∈M)，表示在系统中具有很强的稳定性基本保证从来都不失效的全体执行器所组成的集合，于是有Bi=()(i∈M)，其中BΩi，是分别将对应于，Ωi的列元素取0得到.系统运行中实际的执行器失效集为ωi，ωi⊆Ωi，，为未失效执行器集合，则有下列不等式成立:

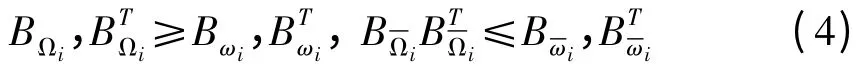
2 可靠控制器设计与优化

定理1 给定性能指标γ＞0，对于系统(1)若给定一组正数εi，ηi，ζi，ρi，αi，ξi，βi，μi，使得下列矩阵不等式组

式中:

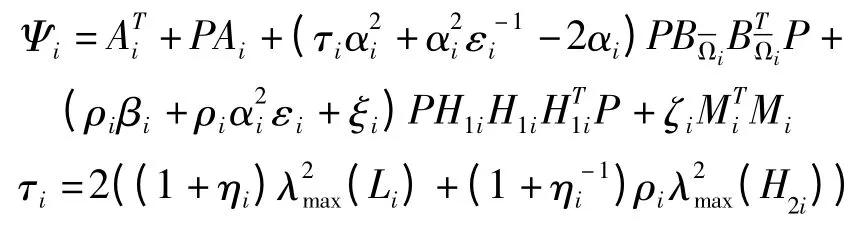
有正定解矩阵P，则系统(1)在任意切换律下是二次稳定的，且存在鲁棒H∞次优可靠控制器，即系统对执行器失效以及参数不确定性具有抑制性与鲁棒性，控制器ki=-αiP.

证明:在任意切换律以及∀x∈Rn{0}下，取公共李雅普诺夫函数V(x)=x(t)TPx(t)，并且假设失效执行器的输出为0，此时ki=-αiP..李雅普诺夫函数沿系统(1)的轨线的导数为:

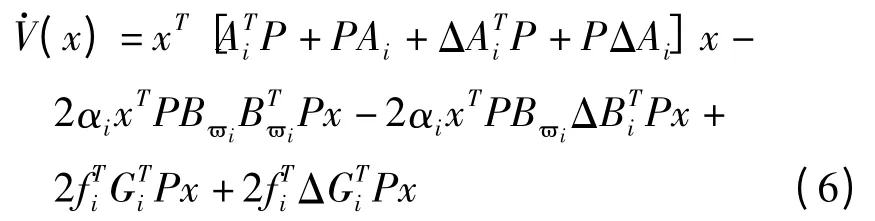
由引理1、引理2得

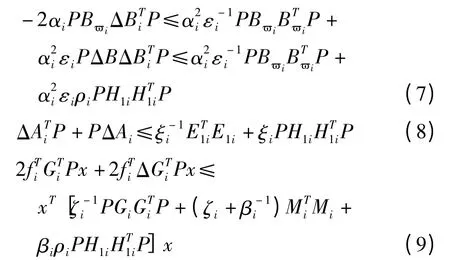
将式(7)～(9)带入式(6)并由式(4)得

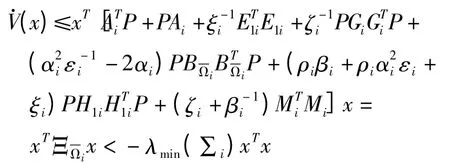
式中:

显然Σi＞0，λmin(Σi)代表矩阵的最小特征值，取ϑ=min{λmin(Πi)}，得到(x)＜-ϑxTx.由于∀i∈M，根据李雅普诺夫函数方法可知，系统(1)二次稳定.

记

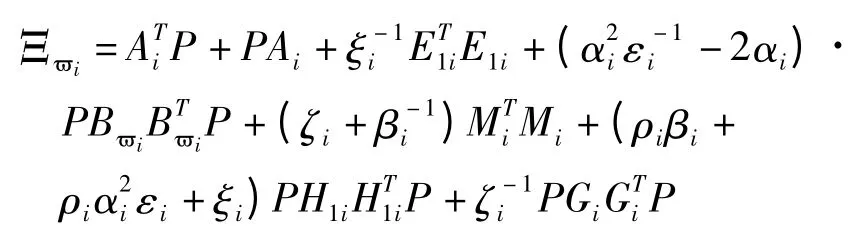
切换信号σ(t):{(0，i(0))，(t1，i(1))，…，(tk，i(k))}，k={1，2，…，m}表示时刻tk第i(k)个子系统在tk时刻运行.对∀T＞0且T∈［tk，tk+1)，在零初始条件下，且扰动w∈L2［0，∞)，类似于文献［6］的证明方法，可以得到:

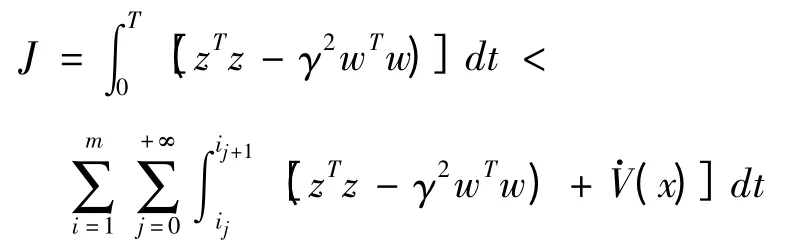
得

记:

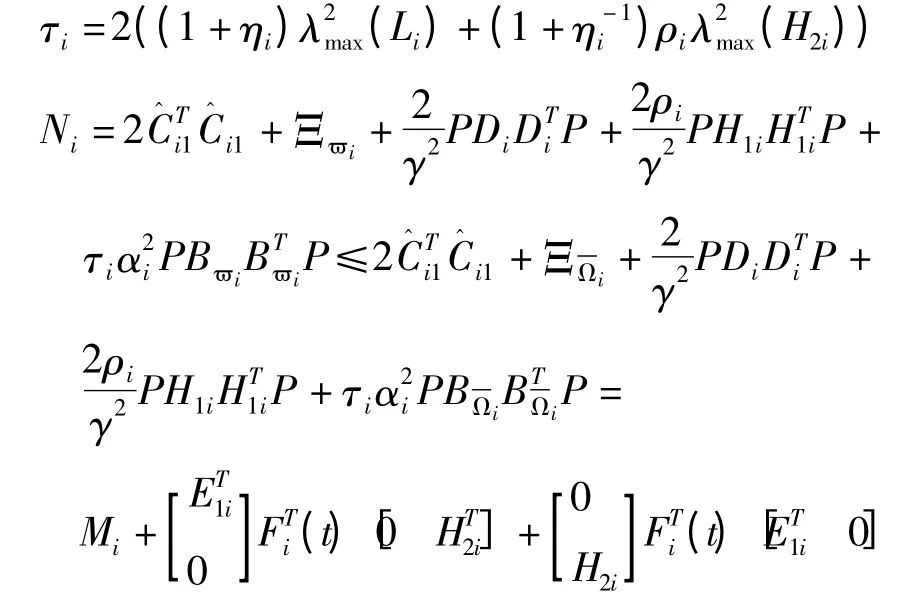
其中:

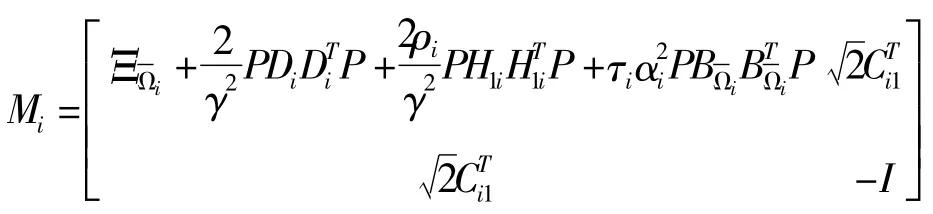
如果Ni＜0，那么系统可解.由引理3可知Ni＜0可以等价为

即

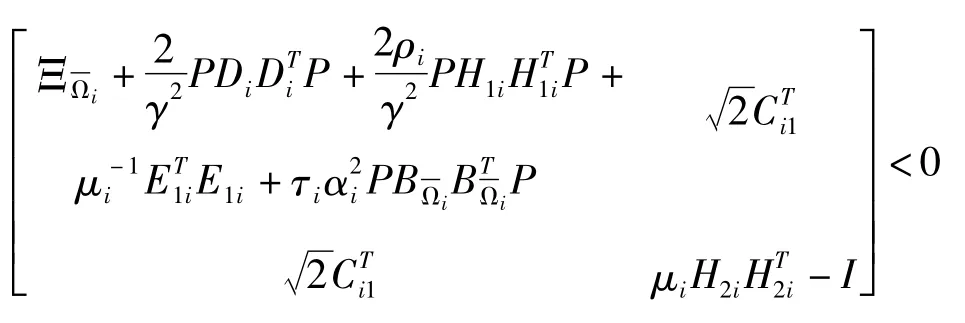
一定存在适当的常数μi＞0使得μiH2i-I＜0，由Schur补引理可知满足定理条件时J＜0，系统(1)H∞鲁棒可靠控制可解，定理证毕.

注1:由于式(5)是双线性矩阵不等式，无法直接求解因此通过引入辅助变量Qi进行化简，使Qi代替定理1中的项，(4)式依然成立.

推论1 对于切换系统(1)，如果给定正数ρi，αi，若以下最优化问题

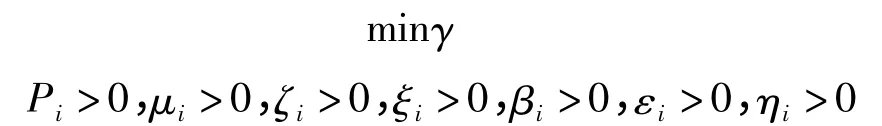
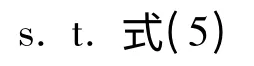
有可行解，则系统(1)在任意切换律下，对于系统允许的参数不确定是二次稳定的，且存在鲁棒H∞最优可靠控制器，即系统满足最小干扰衰减指标γ，控制器其中X-1是定理1的最优可行解.

注2:由于非线性项存在于式(5f)中，因此求解时不便于运算，因此将注1中结论带入定理1中的式(5f)中，并对式(5f)分别做左乘与右乘矩阵diag(P-1，I，I，I，I，I，I，I)，并记=v由Schur补引理可得

其中:

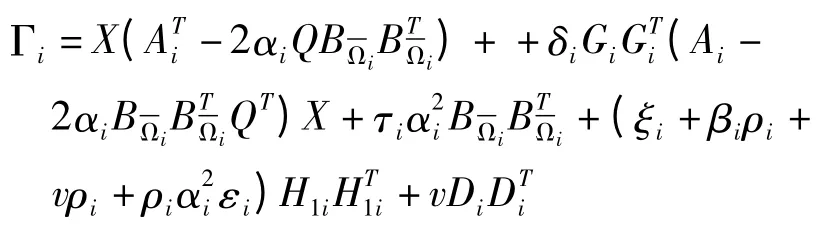
利用矩阵变换技术，上式等价于式(5f)，鲁棒H∞最优可靠控制器

在定理1中我们假设执行器失效时输出信号大小为零，但很多时候故障执行器输出可能不为零，因此假设失效执行器的输出为任意能量有界的干扰信号，属于L2［0，∞］.令为失效执行器的输出信号矢量.此时故障执行器输出被定义为干扰信号，那么系统(1)将为如下形式

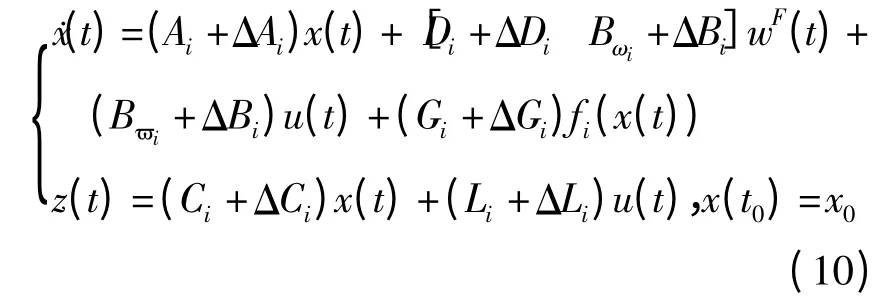
定理2 对于切换系统(10)，指定性能指标γ＞0，若给定一组正数ζi，ρi，αi，ξi，βi，μi，εi，使得下列矩阵不等式组成立

其中:

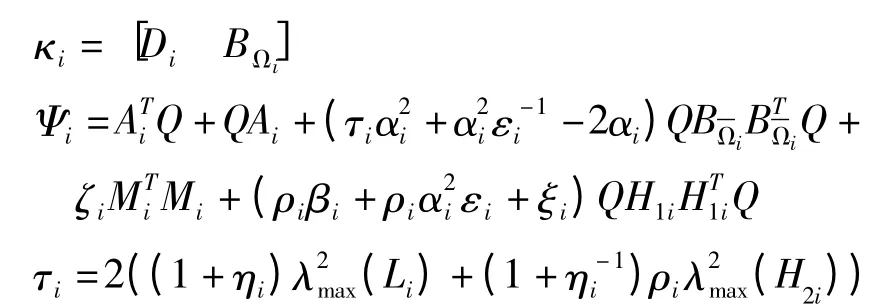
并且有解矩阵Q，其中Q为正定矩阵，则系统(10)在任意切换律下，对于系统允许的参数不确定是二次稳定的，且存在鲁棒H∞次优可靠控制器，控制器

证明:过程参照定理1.

注3:在设计控制器时，在控制器中都存在参数αi，可以通过参数调整使控制器满足系统的要求，十分方便和灵活.

3 仿真算例

考虑由两个子系统组成的不确定非线性切换系统(1)(i=1，2)

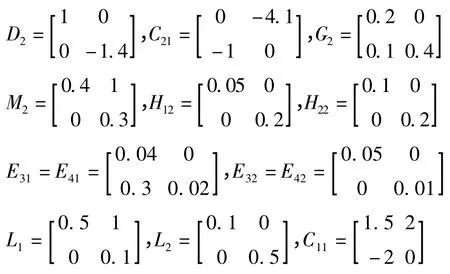
γ=1.5，Ω2=1，Ω1=2，μ1=2，μ2=3，ε1=13，ε1=8，ρ1=ρ2=2，η1=1，η2=4，α1=0.5，α2=0.3，ξ1=6，ξ2=7，β1=8，β2=5，ζ1=ζ2=1.当执行器发生故障时，由定理1的结论，利用LMI工具箱可求得控制器参数为

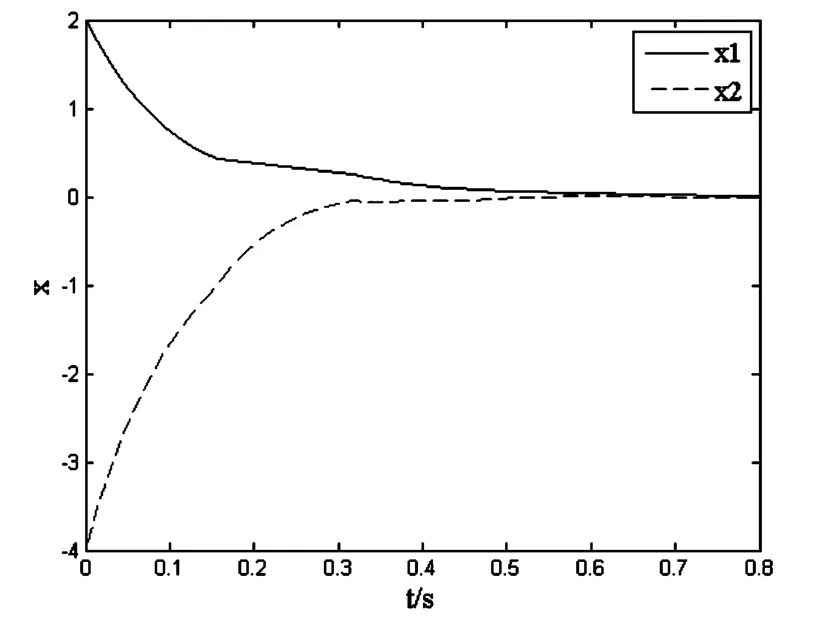
图1 无故障时状态曲线Fig.1 State responses without failure

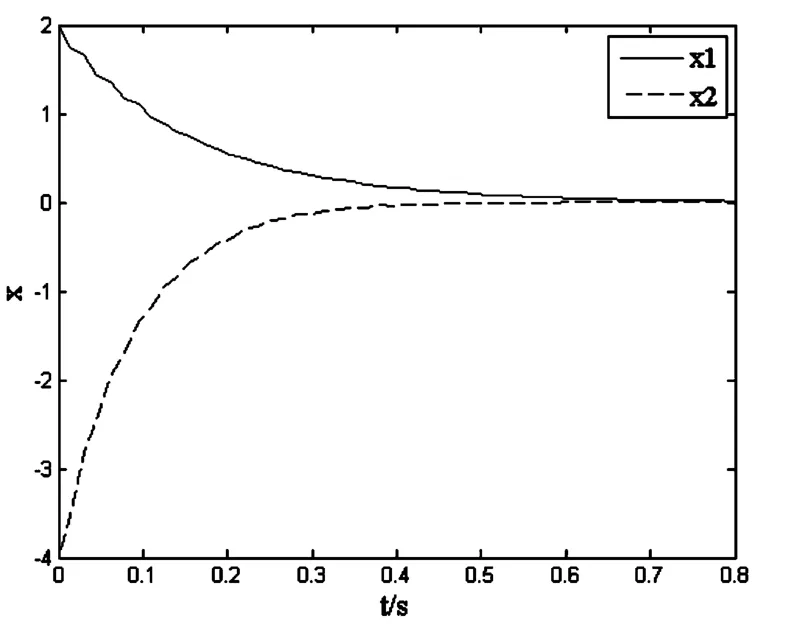
图2 有故障时状态曲线Fig.2 State responses with failure

图1和图2分别给出了执行器正常工作及故障两种情况下，采用可靠控制器时的状态响应曲线.从图中可以看出，两种情况下切换系统均保证稳定且无故障下的系统性能要略好于有故障下的系统性能.

根据推论1以及注2的步骤，利用LMI工具箱计算出最优扰动抑制性能，鲁棒最优可靠控制器为

4 结语

本文针对一类含有外部扰动和所有系统矩阵含有不确定性的非线性切换系统，在执行器发生故障使得系统不稳定的情况下，对系统的可靠控制问题进行研究.利用公共李雅普诺夫法在任意随机切换律下，以LMI的形式给出了系统执行器故障信号输出为零和不为零时的可靠控制器存在的充分条件，同时对系统的扰动抑制性能进行了最优化求解.最后仿真结果表明所设计的控制器在执行器正常工作和一些执行器发生故障时是有效的.

1 向峥嵘，王春芳.一类含阶跃干扰的切换系统最优控制.动力学与控制学报，2008，6(2):138～140(Xiang Z R，Wang CF.Optimal control for a class of switched systems with step perturbations.Journal of Dynamics and Control，2008，6(2):138～140(in Chinese))

2 向峥嵘，王春芳.一类离散线性切换系统的最优控制.动力学与控制学报，2008，6(1):9～11(Xiang Z R，Wang C F.Optimal control for a class of discrete linear switched systems.Journal of Dynamicsand Control，2008，6(1):9～11(in Chinese))

3 Lee J，Bohacek S，Hespanha JP.Modeling communication networks with hybrid systems.IEEE/ACM Transactions on Networking，2007，15(3):630～643

4 李春娟，何墉.一类线性切换系统的非脆弱控制器设计方法.计算技术与自动化，2010，29(2):11～14(Li CJ，He Y.Design methods of non-fragile controllers for a class of linear switched systems.Computing Technology and Automation，2010，29(2):11～14(in Chinese))

5 孙文安，朱晶，陈英等.一类不确定切换系统的容错控制与极点配置.计算技术与自动化，2012，31(2):1～6(Sun W A，Zhu J，Chen Y，et al.The fault-tolerant control and assignment for a class of uncertain switched systems.Computing Technology and Automation，2012，31(2):1～6(in Chinese))

6 Lu J F，Wu Zh M，Jia Y G.Robust reliable control for a class of uncertain switched linear systems.International Journal of Image Graphics and Singnal Processing，2011，3(2):23～29

7 洪晓锋，孙洪飞.切换系统容错控制的研究.厦门大学学报(自然科学版)，2007，46(2):183～186(Hong X F，Sun H F.Study on fault-tolerant control of switched systems.Journal of Xiamen University(Natural Science)，2007，46(2):183～186(in Chinese))

8 汪锐，刘建昌，赵军.一类线性不确定切换时滞系统的可靠保成本控制.控制理论与应用，2006，23(6):1001～1004(Wang R，Liu J C，Zhao J.Reliable guaranteedcost control for a class of uncertain switched linear systems with time-delay.Control Theory＆Applications，2006，23(6):1001～1004(in Chinese))

9 Song Y，Xiang Z R，et al.Robust reliable control of switched uncertain systems with time-varying delay.International Journal of Systems Science，2006，37(15):1077～1087