神经元膜电位噪声取值范围的评估

王如彬 王关政 倪力 郑锦超

(华东理工大学理学院和信息学院认知神经动力学研究所，上海 200237)

引言

神经系统中的热噪声对于信息处理至关重要并且影响着中枢神经系统工作的所有方面［1-6］.如何评估神经系统中这类噪声的强度对网络行为的影响以及认知功能的作用一直是科学家们所十分关注的一个问题［7-11］.然而，到目前为止在已发表的科学文献中所有对神经元或神经网络中噪声大小的选择都带有随意性，也就是说对噪声强度的选择依据没有做出任何的说明，在有些情况下作者们常常依据希望得到的数值计算结果来选择噪声的大小.如何科学地确定神经系统中的噪声性质以及噪声大小的范围是一个十分困难的问题［12-18］.虽然大量的发表已经从定量的角度研究了噪声条件下的神经元或神经网络的信息编码以及它们的动力学行为［9-18］，但是都没有涉及到一个最基本问题-噪声数值范围的取值依据.因此从理论上讲这些数值计算结果理所当然地会与实验数据有一定的偏差，从神经编码的角度而言其数值计算结果的有效性也需要进一步讨论.考虑到上述这些情况，本文在文献［19-21］的基础上，用能量方法研究各种膜电位以及它们各自对应的能量波形在噪声影响下的取值范围，从而确定对这些神经能量波形产生显著影响的噪声临界值的估计范围.研究思想的主要依据是，既然不可能通过实验测量到影响脑内神经元活动的噪声水平，那么根据神经元膜电位与能量函数有唯一对应关系的准则，只要给出能够改变神经元能量函数的噪声范围，就可以基本确定这个噪声范围就是实际神经系统中神经元的噪声水平.这是因为你可以通过调整噪声的大小来改变你希望得到的膜电位，但是这个膜电位与真实对应的神经能量并没有直接的内在联系.因此我们从神经能量出发来研究膜电位，观察在什么样的噪声水平下使得膜电位的能量函数发生了根本的改变，那么这个噪声强度的大小就是神经元赖以活动的生理学意义上的噪声环境.

由此可以进一步探讨网络条件下的噪声取值范围.这项研究工作的重要意义在于不仅在建立神经元模型时应当如何正确地选取噪声的大小，而且在考虑建立神经元网络模型时不再具有盲目性，对网络噪声的取值范围也提供了充分的科学依据.最后需要强调的是本文并不考虑噪声大小的相对值，因此不讨论信噪比问题.

1 第1部分神经元的生物物理模型

与传统的简单独立的单个神经元模型相比，图1增加了一个电压源和电流源以及一个电感.电压源是神经元内外各种离子的浓度差所形成的，它将驱使离子的移动.电流源的形成一方面是由于离子的化学梯度的存在，另一方面是神经元会接受周围神经元的刺激.此外，钠离子、钾离子、钙离子等各种带电离子在离子通道中流进流出，会形成一个回路电流，引起自感应效果，等效于一个电感元件Lm.Cm为膜电容，Im表示外部所有与之相连的神经元输入的总电流.U分别表示电压源，rm和r0m分别是跨越Im和U的电阻，是由于电流源和电压源不理想所造成的损耗.由于电流源和电压源的作用位点不是在同一位置，将膜电阻分为了三部分:r1m、r2m和r3m.

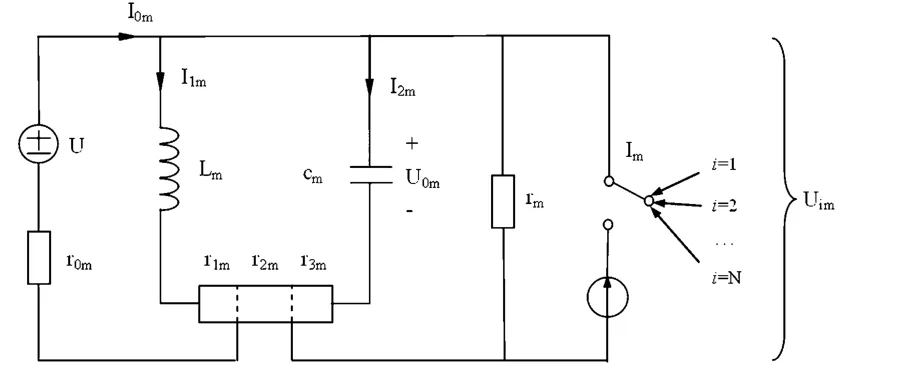
图1 电流耦合下单个神经元的电模型ig.1 Physical model of the MTh neuron with coupling to other neurons

由图1可获得电压源Um和电流源Im提供第m个神经元的功率Pm为

其中

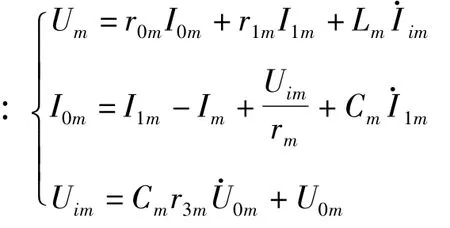
电流源的形式可由下式表示:

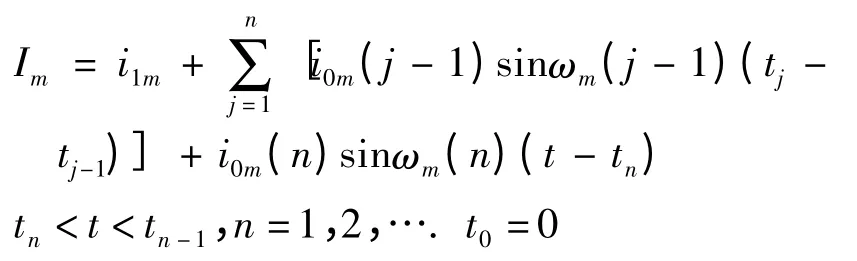
其中i1m为维持静息膜电位所需要的电流，i0m表示神经元在阈下活动时受周围神经元电流刺激而产生的总效应，ωm为动作电位发放频率.

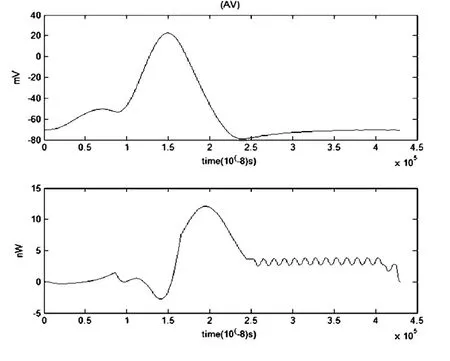
图2 动作电位和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=70.7μAFig.2 Action potential and its corresponding energy function

为简化起见，我们直接给出用能量方法得到的动作电位和对应的用功率表示的神经元能量函数，如图2所示.

由图2可知神经元动作电位的峰值为25mv左右，而能量函数的峰值为12nw左右.

兴奋性突触后电位(EPSP)和抑制性突触后电位(IPSP)所对应的能量波形分别如图3和图4所示:

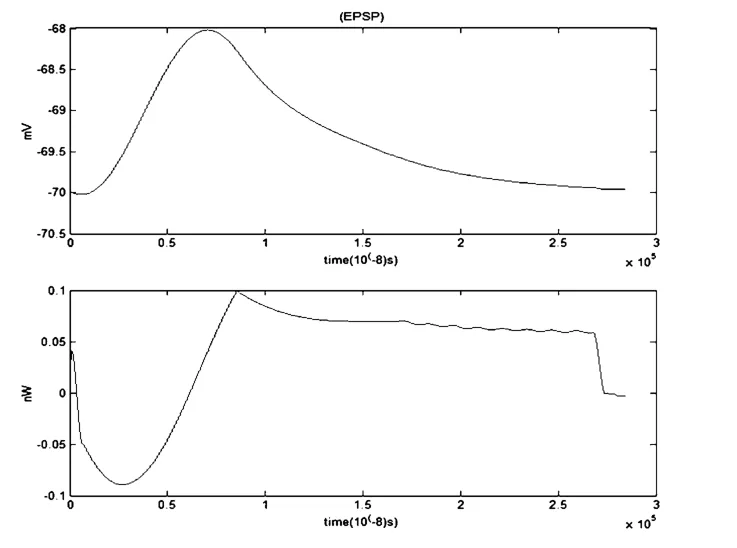
图3 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μAFig.3 EPSP and its corresponding energy function

图4 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μAFig.4 IPSP and its corresponding energy function

在大脑皮层中，兴奋性神经元的比例高达85%，剩下的是抑制性神经元［22］.在阈下情形中，尽管单个神经元EPSP与IPSP的简单叠加的功率是负值(PP=0.0367+(-0.0532)=-0.0165 nw);但从总体上来看，神经系统消耗的能量还是正值(PP’=0.0367×85% -0.0532×15% =0.0232 nw).从这个结果上看，即便神经系统是在阈下活动时，在整体上还是在消耗着外界提供的能量.根据计算结果可以看到，阈上活动的神经元所消耗的能量远大于阈下活动时神经元所消耗的，这个结论与实验结果完全一致［22］.有研究表明，大量在阈下活动的神经元只消耗能量的20%，而少量的在阈上活动的神经元由于发放动作电位而消耗能量的80%以上［22］.根据我们的计算结果，与这个结论是基本吻合的.

2 第2部分脑内噪声环境的评估

单个神经元的功能是在神经网络条件下起作用的，也就是在和其他神经元相互作用的情况下神经元的功能性作用才能得以体现.也正是在这个意义上神经元的活动是在生理学条件下的噪声环境中进行新陈代谢的.为了能够获得神经元活动的噪声水平，进而获得神经网络条件下脑内的噪声环境，我们需要事先了解无噪声情况下神经元膜电位所对应的能量函数［19］，只有在获得了理想条件下的神经能量，才有可能进一步了解生理学意义上的噪声对神经元膜电位及神经能量的影响.在这个基础上，我们才有可能深入了解网络条件下神经系统的噪声环境以及在这样一种噪声环境下对网络行为进行评估.

2.1 阈上膜电位与神经能量

如果在电流i0m上增加一个高斯白噪声，当噪声值大于10-4μA时，噪声对膜电位i0m及能量函数的影响远远大于电流对膜电位及能量函数的影响，当噪声小于10-7μA时，噪声对膜电位及能量函数的影响远远小于电流i0m对膜电位及能量函数的影响.因此取噪声的大小分别为:10-4μA，10-5μA，10-6μA，，

其中加入高斯白噪声后电流形式变为

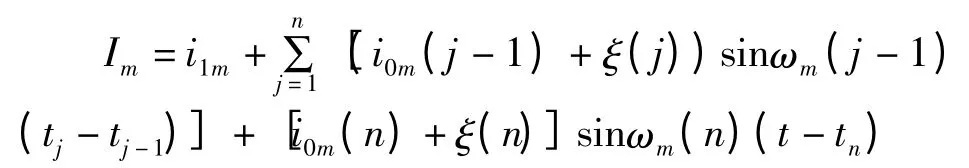
其中符号ξ(j)为高斯白噪声定义的突触噪声，单位为μA.满足以下二阶矩条件:

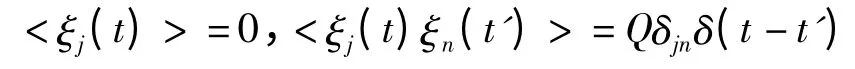
下面是用能量方法在不同噪声大小情况下得到的动作电位及对应的用功率表示的能量函数:

当噪声大小为10-4μA时，神经元膜电位的峰值为180 mv左右，远大于无噪声影响时的25 mv.而能量函数的峰值在70 nw左右，远大于原来的12 nw.其次在横坐标的时间轴上，在2.5毫秒至4毫秒之间，能量波形的振荡幅度也要比没有噪声时的能量波形振荡幅度要大得多.由此可见当噪声大小为10-4μA时，从根本上改变了理想条件下的动作电位和对应的能量函数.

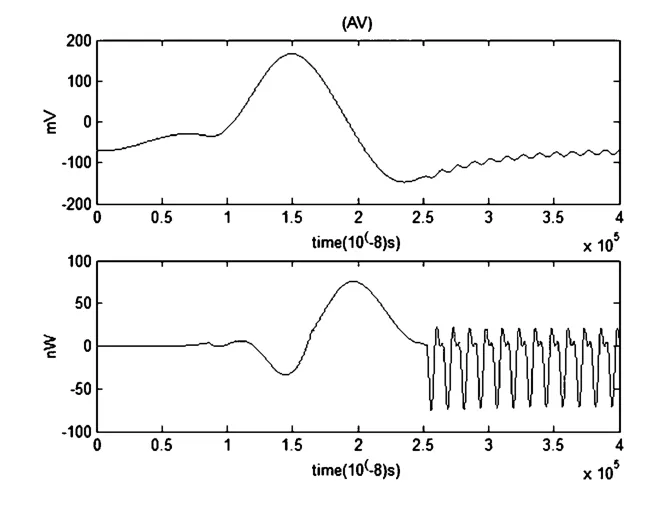
图5 动作电位和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=70.7μA，Q=1×10-4μAFig.5 The action potential and its corresponding energy function

图6 动作电位和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=70.7μA，Q=1×10-5μAFig.6 The action potential and its corresponding energy function

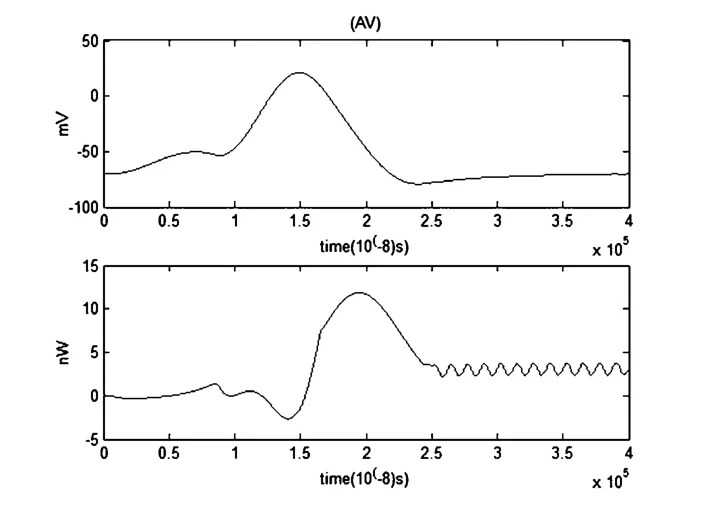
图7 动作电位和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=70.7μA，Q=1×10-6μAFig.7 The action potential and its corresponding energy function

当噪声大小为10-5μA时，噪声对动作电位及其功率的影响虽减小但仍然明显.此时膜电位为10mv左右，而能量函数的峰值为8nw左右.可以看出，该噪声水平对膜电位的大小和对应的能量波形还是有明显的影响.

但是当噪声大小为10-6μA时，噪声对动作电位及其功率函数几乎没有影响.也就是说在这样一种噪声环境下，膜电位的峰值和能量波形的峰值与理想条件下的情况完全一致，即动作电位和能量函数的峰值分别为25mv与12nw.加入噪声后膜电位及能量函数的波形与不加噪声时的波形几乎重合.

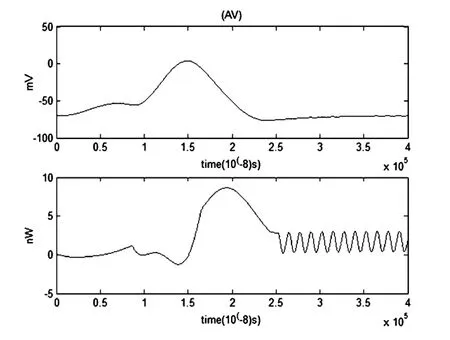
图8 动作电位和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=70.7μA，Q=6×10-6μAFig.8 The action potential and its corresponding energy function

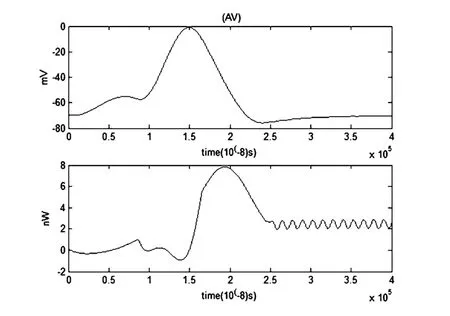
图9 动作电位和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=70.7μA，Q=6×10-6μAFig.9 The action potential and its energy function

综上所述，我们无法找到阈上膜电位与神经能量的噪声估计值.为了能准确地找到噪声临界值的估计范围，发现当噪声大小为6×10-6μA左右(误差值±0.5×10-6μA)时，噪声开始对动作电位和对应的能量函数产生显著影响.

根据图8，9，10可见，当噪声大小为6×10-6μA时，膜电位和能量函数起伏波动很大.动作电位的峰值在0mv至45mv之间波动，而能量函数的峰值在8nw至17nw之间波动.可见噪声对膜电位及能量函数影响明显.可判定阈上膜电位的噪声临界值为6×10-6μA(误差值±0.5×10-6μA)

2.2 阈下膜电位与神经能量

根据文献［21］的计算结果，这里通过加入噪声后得到了兴奋性突触后电位(EPSP)及对应的能量波形和抑制性突触后电位(IPSP)及对应的能量波形如图11至图25所示.

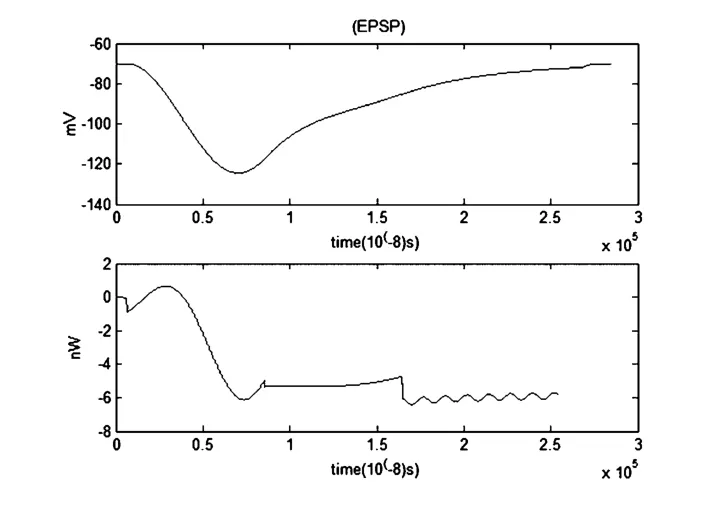
图11 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=1×10-4μAFig.11 The EPSP and the corresponding energy function

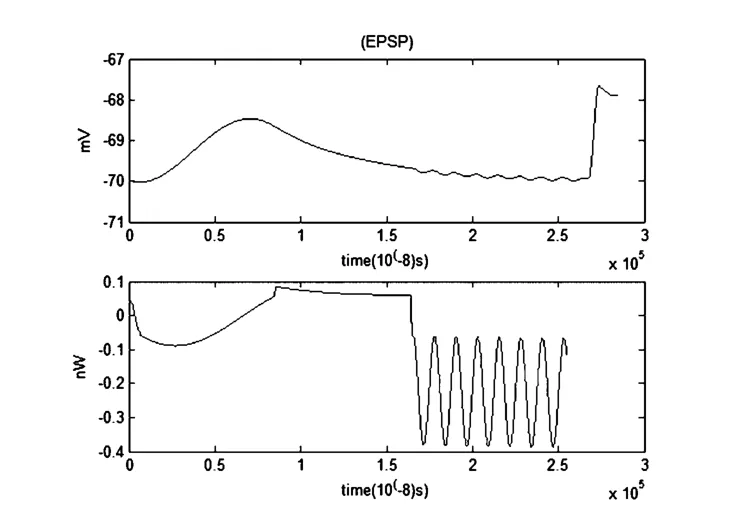
图12 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=1×10-5μAFig.12 The EPSP and the corresponding energy function

当噪声大小为1×10-4μA时，噪声对兴奋性突触后电位(EPSP)和对应的能量波形影响非常大.不考虑噪声影响时，EPSP曲线先上升再下降，最大值为-68mv，最小值为-70mv，能量函数先下降后上升最后趋于稳定，在-0.1nw至0.1nw范围内波动.加入上述噪声后EPSP曲线为先下降再上升，最小值达到-130mv，而能量函数先上升后下降最后趋于稳定，在-7nw至1nw范围之间波动.

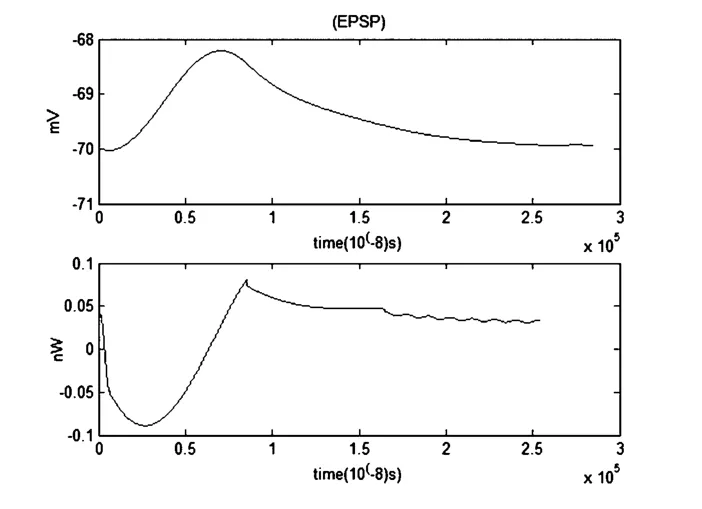
图13 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=1×10-6μAFig.13 The EPSP and the corresponding energy function

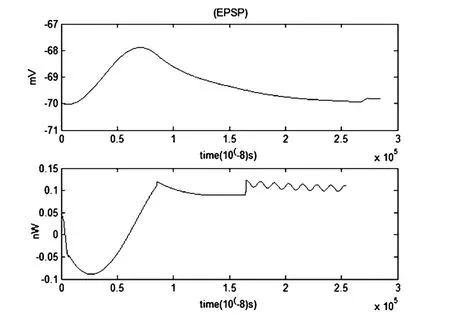
图14 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=2×10-6μAFig.14 The EPSP and the corresponding energy function

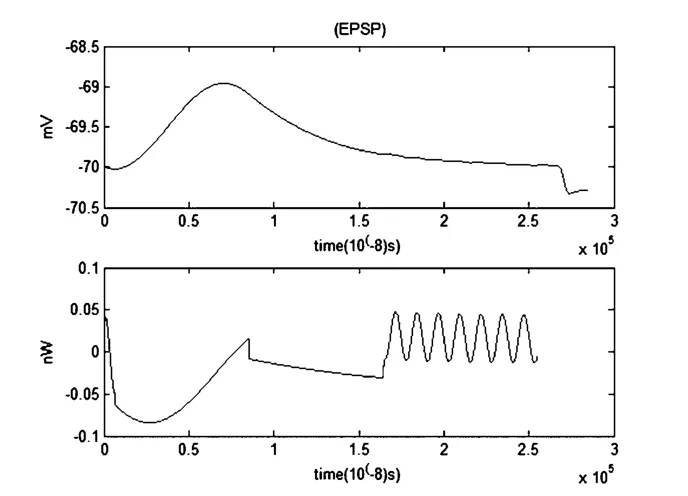
图15 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=3×10-6μAFig.15 The EPSP and the corresponding energy function

当噪声大小为1×10-5μA时，噪声对兴奋性突触后电位(EPSP)和对应的能量波形影响仍然十分明显.在没有噪声的理想条件下，已知EPSP的最大值为-68mv左右，能量函数的峰值为0.1nw左右.在该噪声条件下，EPSP峰值虽变化不大，但在时间轴上的2.5至3毫秒期间，振荡曲线发生突变.而能量函数1.5至2.5毫秒之间时，能量函数的振荡幅度要比没有噪声影响时的振荡幅度剧烈的多.

当噪声大小为1×10-6μA时，噪声对兴奋性突触后电位(EPSP)和对应的能量波形影响不大.与不考虑噪声时的EPSP及能量函数图像基本重合.根据图11至图13，我们无法找到影响EPSP所对应的能量函数的噪声临界值的范围.

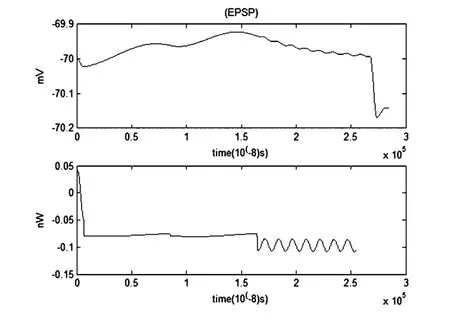
图16 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=3×10-6μAFig.16 The EPSP and the corresponding energy function

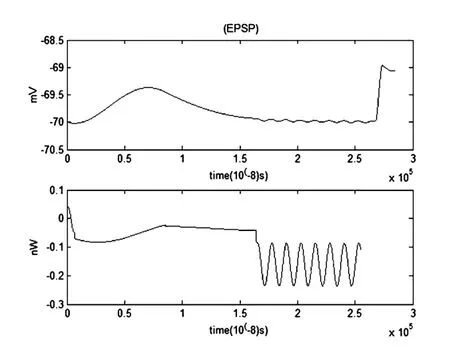
图17 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=3×10-6μAFig.17 The EPSP and the corresponding energy function

为了能准确地找到临界值的估计范围，可以通过改变噪声强度的系数来进行探讨.

当噪声大小为2×10-6μA时，噪声对兴奋性突触后电位(EPSP)和对应的能量波形没有显著影响.考虑噪声时的EPSP及能量函数与不考虑噪声时的EPSP及能量函数图像基本重合.但是在1.5至2.5毫秒之间，有噪声时能量函数与没有噪声时的情况略有不同.

当噪声大小为3×10-6μA时，噪声不仅对兴奋性突触后电位(EPSP)的波形有显著影响，而且对其对应的能量波形影响也非常大.考虑噪声时EPSP几乎只在-69mv至-70mv这一很小的区间内波动，横坐标在区间2.5毫秒至3毫秒之间EPSP的值产生突变.而在1.7毫秒至2.5毫秒期间，能量函数的波形与没有噪声时的理想情况相比有剧烈的波动.

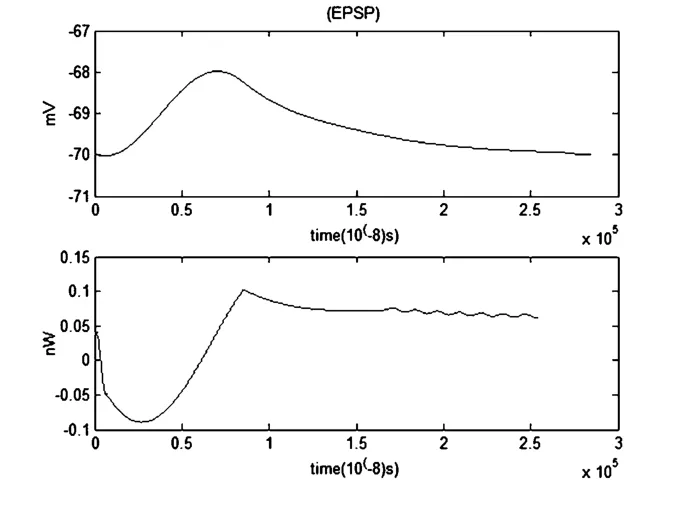
图18 EPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=7.155μA，Q=1×10-7μAFig.18 The EPSP and the corresponding energy function

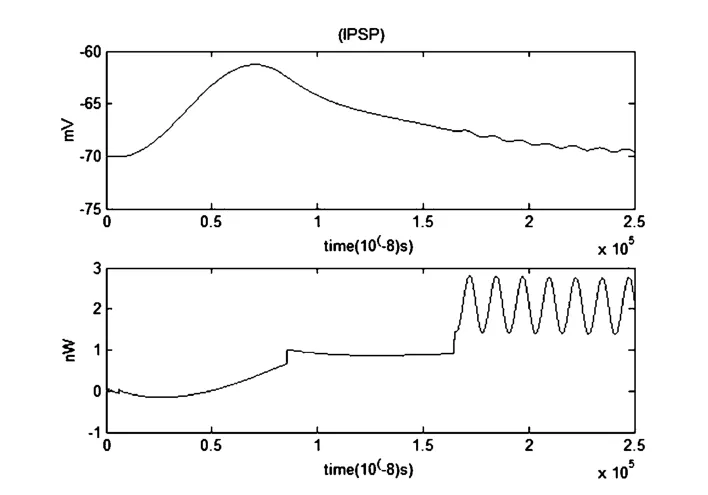
图19 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μA，Q=1×10-4μAFig.19 The IPSP and the corresponding energy function

但是当噪声大小为1×10-7μA时，噪声对兴奋性突触后电位(EPSP)和对应的能量波形几乎没有影响.考虑噪声时的EPSP及能量函数与没有噪声时的EPSP及能量函数图像基本重合.

综上可知，当噪声大小为3×10-6μA左右(误差值±0.5×10-6μA)时，噪声开始对兴奋性突触后电位(EPSP)及对应的能量波形产生显著的影响.为此取噪声的临界值为3×10-6μA，(误差值±0.5×10-6μA)

当噪声大小为1×10-4μA时，噪声对抑制性突触后电位(IPSP)和对应的能量波形有很大影响.不考虑噪声影响时，IPSP曲线先下降再上升，能量函数曲线大部分处于-0.04nw的稳定状态.考虑噪声时IPSP曲线先上升再下降，能量函数的曲线大部分处于0之上，且横坐标在区间1.5毫秒至2.5毫秒期间能量的波动是非常大的.

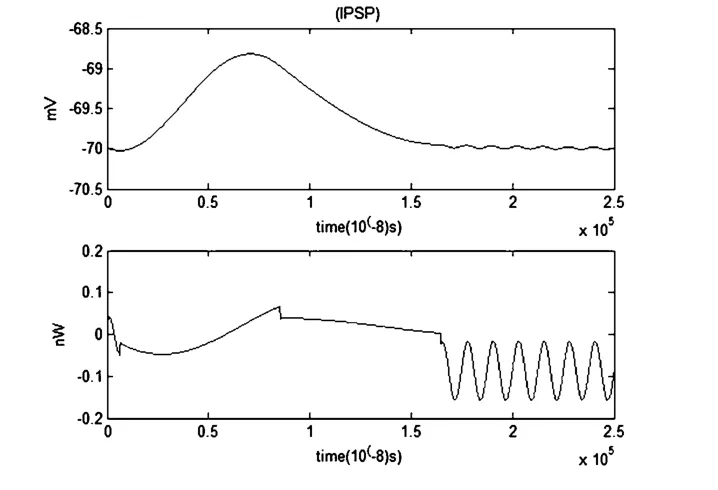
图20 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μA，Q=1×10-5μAFig.20 The IPSP and the corresponding energy function

当噪声大小为1×10-5μA时，噪声对抑制性突触后电位(IPSP)和对应的能量波形有很大的影响.不考虑噪声影响时，IPSP曲线先下降再上升，能量函数曲线大部分处于-0.04nw的稳定状态.考虑噪声时IPSP曲线先上升再下降，横坐标在1.5毫秒至2.5毫秒时能量函数的曲线波动幅度是非常大的.

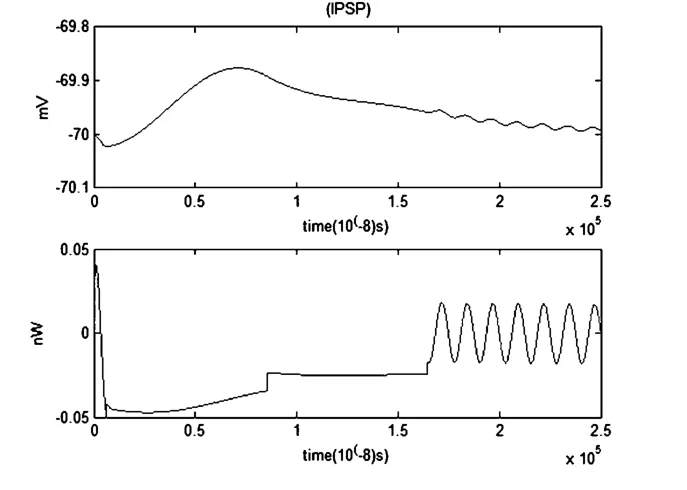
图21 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μA，Q=1×10-6μAFig.21 The IPSP and the corresponding energy function

当噪声大小为1×10-6μA时，噪声对抑制性突触后电位(IPSP)和对应的能量波形有较大影响.不考虑噪声影响时，IPSP曲线先下降再上升，能量函数曲线大部分处于-0.04nw的稳定状态.考虑噪声时IPSP曲线先上升再下降，横坐标在1.5毫秒至2.5毫秒时能量函数的曲线波动幅度也非常大.

当噪声大小为1×10-7μA时，噪声对抑制性突触后电位(IPSP)和对应的能量波形几乎无影响.考虑噪声时的IPSP及能量函数与不考虑噪声时的IPSP及能量函数图像基本重合.

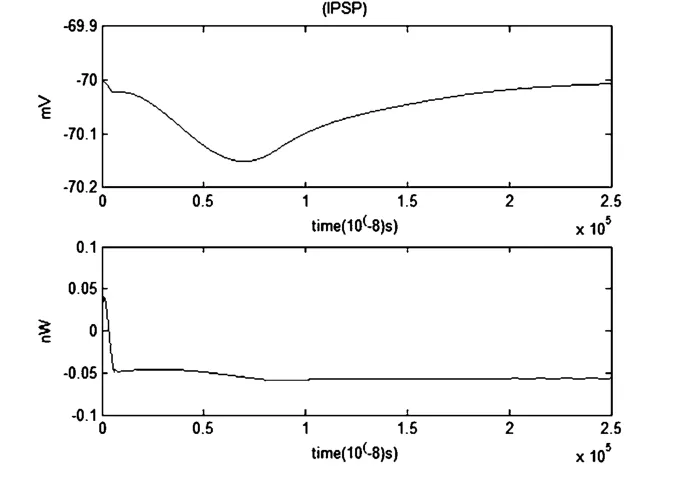
图22 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μA，Q=1×10-7μAFig.22 The IPSP and the corresponding energy function

根据图19至图22，我们无法找到影响IPSP所对应的能量函数的临界值范围.

为了能准确地找到临界值的估计范围，可以通过改变噪声强度的系数来进行探讨.

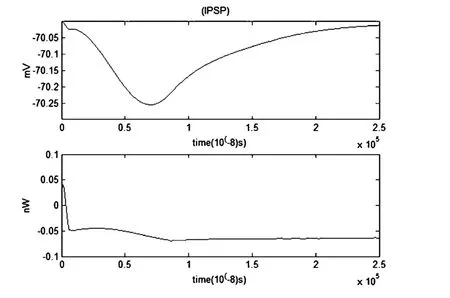
图23 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μA，Q=2×10-7μAFig.23 The IPSP and the corresponding energy function

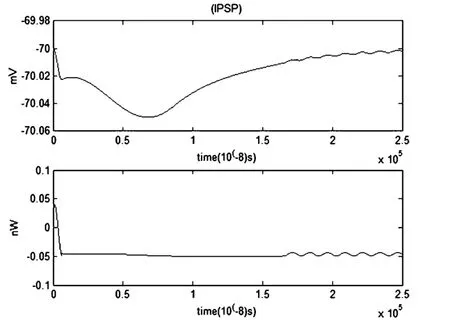
图24 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μA，Q=3×10-7μAFig.24 The IPSP and the corresponding energy function

当噪声大小为2×10-7μA时，噪声对抑制性突触后电位(IPSP)和对应的能量波形无显著影响.考虑噪声时的IPSP及能量函数与不考虑噪声时的IPSP及能量函数图像基本重合.

当噪声大小为3×10-7μA时，噪声对抑制性突触后电位(IPSP)和对应的能量波形无显著影响.考虑噪声时的IPSP及能量函数与不考虑噪声时的IPSP及能量函数图像基本重合.

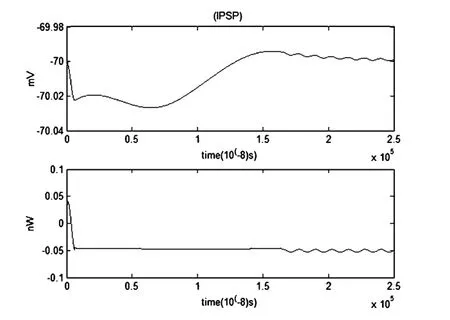
图25 IPSP和对应的能量函数r0m=0.0001Ω，r1m=0.1Ω，r2m=1000Ω，r3m=0.1Ω，rm=1000Ω，Cm=1μF，Lm=50μH，i0m=-0.7μA，Q=4×10-7μAFig.25 The IPSP and the corresponding energy function

当噪声大小为4×10-7μA左右(误差值±0.5×10-7μA)时，噪声对抑制性突触后电位(IPSP)及对应的能量波形开始产生显著影响.不考虑噪声时IPSP的曲线走势为先下降后上升，考虑噪声时，IPSP在［0，0.5］上不是单调递减的，而是在区间1.5毫秒至2.5毫秒期间，能量函数的波形开始出现波动.

综上可知当噪声大小为4×10-7μA左右(误差值±0.5×10-7μA)时，噪声对抑制性突触后电位(IPSP)及对应的能量波形开始产生显著影响.取噪声临界值为4×10-7μA(误差值±0.5×10-7μA).

3 结论

本文通过在电流上增加高斯白噪声得到了动作电位、EPSP、IPSP及对应的能量波形，通过改变噪声的大小找到噪声对神经元膜电位及对应的能量波形产生显著影响的临界值的估计范围.当噪声大小为左右(误差值)时，噪声对动作电位及对应的能量波形产生显著影响.当噪声大小为(误差值)左右时，噪声对兴奋性突触后电位(EPSP)及对应的能量波形产生显著影响.当噪声大小为左右(误差值)时，噪声对抑制性突触后电位(IPSP)及对应的能量波形产生显著影响.通过对噪声临界值的比较分析发现:噪声对动作电位及对应的能量波形的影响要比对兴奋性突触后电位(EPSP)及对应的能量波形和抑制性突触后电位(IPSP)及对应的能量波形的影响要小.对兴奋性突触后电位(EPSP)及对应的能量波形的影响要比对抑制性突触后电位(IPSP)及对应的能量波形的影响要小.通过数值计算找到了噪声对动作电位、EPSP、IPSP及对应的能量波形产生影响的临界值的估计范围.今后在类似的神经动力学建模中考虑噪声对神经发放的影响时不再具有随意性，以便使计算结果与实验数据具有更好的一致性.因此噪声临界值的估计范围为噪声条件下神经信息编码的研究提供了科学的依据.

1 Aldo A F，Luc P S，Daniel M W.Noise in the nervous system.Nature Review Neuroscience，2008，9:292～303

2 Edmund T R，Gustavo D.The noisy brain:stochastic dynamics as a principle of brain function.Oxford:Oxford University Press，2010

3 Bernasconi F，De Lucia M，Tzovara A，Manuel A L，Murray M M，Spierer L.Noise in brain activity engenders perception and influences discrimination sensitivity.Journal of Neuroscience，2011，31(49):1797～81

4 Mori T，Kai S.Noise-induced entrainment and stochastic resonance in human brain waves.Physical Review Letters，2002，88:218101

5 Wennekers T，Plam G.Syntactic sequencing in Hebbian cell assemblies.Cognitive Neurodynamics，2009，3(4):429～441

6 Werner G.From brain states to mental phyenomena via phase spase transitions and renormalization group transformation:proposal of a theory.Cognitive Neurodynamics，2012，6(2):203～209

7 Gustavo K R，Alan T S.Estimating intensity variance due to noise in registered images:applications to diffusion tensor MRI.NeuroImage，2005，26:673～684

8 Hunt D，Korniss G，Szymanski B K.Network synchronization in a noisy environment with time delays:fundamental limits and trade-offs.Physical Review Letters，2010，105:068701

9 Decoa G，Jirsac V，McIntoshe A R，Spornsf O，Kotter R.Key role of coupling，delay，and noise in resting brain fluctuations.Proceeding of National Academy Science，2009，106(25):10302～10307

10 Wang R B，Zhang Z K.Phase synchronization motion and neural coding in dynamic transmission of neural information.IEEE Transactions on Neural Networks，2011，22(7):1097～1106

11 Zhang X D，Wang R B，Zhang Z K.Dynamic phase synchronization characteristics of variable high-order coupled neuronal oscillator population.Neurocomputing，2010，73:2665～2670

12 Jiao X F，Wang R B.Synchronous firing patterns of neuronal population with excitatory and inhibitory connections.International Journal of Non-Linear Mechanics，2010，45:647～651

13 Gao JB，Hu J，Tung WW.Complexity measures of brain wave dynamics.Cognitive Neurodynamics，2011，5(2):171～182

14 Liu Y，Wang R B，Zhang Z K，Jiao X F.Analysis on stability of neural network in the presence of inhibitory neurons.Congnitive Neurodynamics，2010，4(1):61～68

15 Huand M，Liang H L.Noise-assisted instantaneous coherence analysis of brain connectivity.Computational Intelligence and Neuroscience，2012，12:275073

16 Tass P A.Phase resetting in medicine and biology.Modelling and Data Analysis.Berlin:Springer-Verlag，1999

17 Ghosh A，Rho Y，McIntosh A R，Kötter R，Jirsa V K.Noise during rest enables the exploration of the brain＇s dynamic repertoire.Public Library of Science Computational biology，2008，4(10):e1000196

18 Maye A，Hsieh C H，Sugihara G，Brembs B.Order in spontaneous behavior.Public Library of Science ONE，2007，2(5):e443

19 Wang R B，Zhang Z K，Jiao X F.Mechanism on brain information processing:energy coding.Applied Physics Letters，2006，89:123903

20 Wang R B，Zhang Z K.Energy coding in biological neural network.Cognitive Neurodynamics，2007，1(3):203～212

21 Wang R B，Zhang Z K，Chen G R.Energy coding and energy functions for local activities of brain.Neurocomputing，2009，73(1-3):139～150

22 Marcus E R，Debra A G.Appraising the brain’s energy budget.Proceeding of National Academy Science，2002，99(16):10237～10239