复杂动力学网络的自适应线性广义同步及参数识别*

毕海静 张荣† 何雪明

(1.江南大学理学院，无锡 214122)(2.江南大学江苏省食品先进制造装备技术重点实验室，无锡 214122)

引言

最近20多年来，由于混沌同步的理论价值和其在各个领域中的潜在应用，使得这方面的研究受到广泛关注，提出了各种实现完全同步的方法［1-5］，然而，在实际应用中，参数的失配可能破坏完全同步流形，而且完全同步仅发生在参数空间的某个特定点上，所以除非在理想条件下它是很难实现的，进而人们研究许多不同类型的同步［6-12］.在各种不同类型的同步中，广义同步［13］是指耦合混沌振子之间存在某种函数关系，可见广义同步是完全同步的拓广，因而广义同步在理论价值和潜在应用方面更有普遍性.因此广义同步成为研究热点之一，取得了一些研究结果［14-16］，这些结果大致可以分为两类:一是设计适当的控制器使耦合的系统之间满足给定的函数关系;二是辅助系统方法，此方法已被广泛用于检测两个耦合的混沌系统的广义同步.

本文的工作可归于第一类，是针对参数未知的复杂动力学网络，通过设计合适的自适应控制器实现了复杂动力学网络之间的线性广义同步.一个复杂动力学网络是由一系列相互连接的节点组成的，其中每个网络节点是一个动力系统，它是处理一组相互作用的动力系统的一个很好的工具，复杂动力学网络广义同步的研究工作包括用拓展辅助系统的方法来实现复杂网络的广义同步［17-19］，通过构建适当的响应网络使驱动响应网络之间满足预先给定的函数关系［20-21］.最近，Sun等人研究了已知参数的两个复杂网络之间的线性广义同步［22］，受此工作启发，本文探讨了未知参数的复杂动力学网络的自适应线性广义同步.实际中复杂动力学网络不可避免受到如噪声和参数变动等不确定因素的影响，因此研究参数未知的不确定复杂动力学网络的同步问题有重要意义.本文设计的自适应控制器不仅实现了复杂动力学网络之间的线性广义同步，而且对网络中的未知参数进行了追踪识别，适用于一类未知参数的复杂动力学网络.

1 问题描述

考虑驱动复杂网络

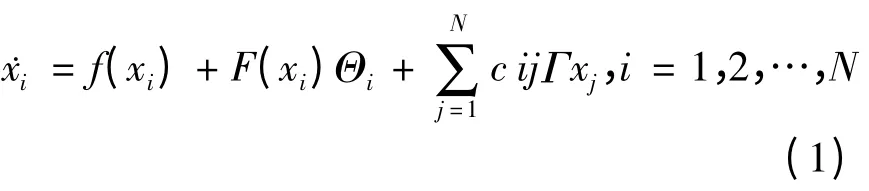
其中xi(t)=(xi1(t)，xi2(t)，…，xin(t))T∈Rn，f(x):Rn→Rn，F(x):Rn→Rn×p为非线性函数，Θi=(θi1，θi2，…，θip)T∈Rp为 未 知 参 数 矢 量.C=(cij)N×N∈RN×N为耦合矩阵，节点i和节点j(j≠i)耦合时，cij=1;否则cij=0(j≠i)，且i=1，2，…，N.Γ∈Rn×n为内耦合矩阵.

响应复杂网络

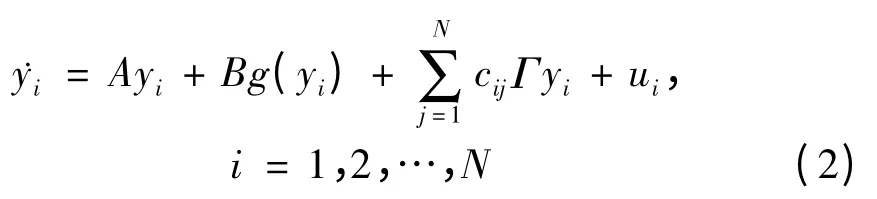
其中yi(t)=(yi1(t)，yi2(t)，…，yin(t))T∈Rn，ui为控制器.

定义 对驱动网络(1)和响应网络(2)，若存在映射φ:Rn→Rn满足

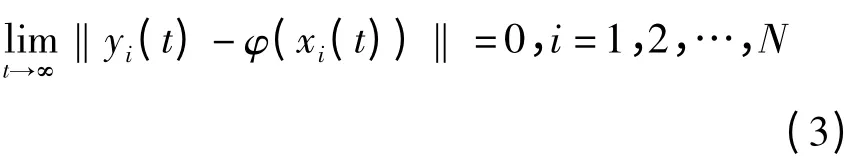
则称网络(1)和(2)实现广义同步.特殊地若φ(x)=Px+Q(P和Q是两个常数矩阵)，则称网络(1)和(2)实现线性广义同步.

2 线性广义同步实现

定义线性广义同步误差为

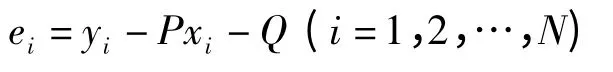
定理 假定驱动响应网络(1)(2)满足PΓ=ΓP及以下条件:

(ⅰ)‖A‖≤α，‖B‖≤β，‖Γ‖=γ;

(ⅱ)对任意不同的z1，z2∈Rn，有常数L，使‖g(z1)-g(z2)‖≤L‖z1-z2‖，若取自适应控制器ui为

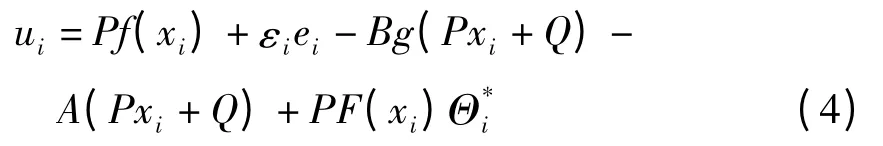
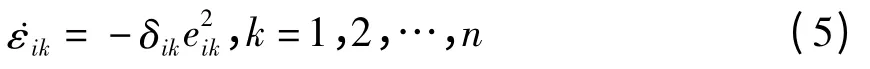
参数值由下式追踪识别:

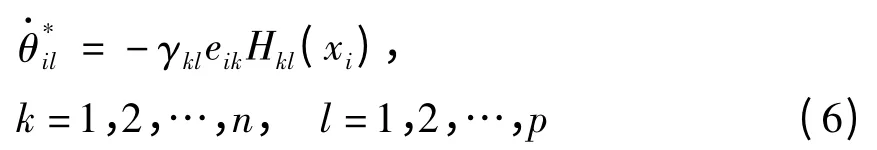
其中H(x)=(Hkl(x))n×p=PF(x)，δik＞0，γkl＞0为任意常数.则网络(1)和(2)实现线性广义同步.

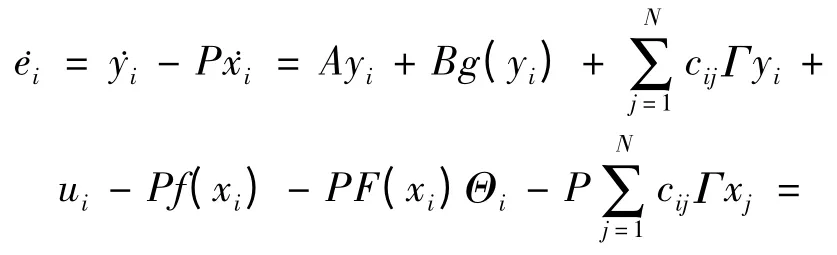
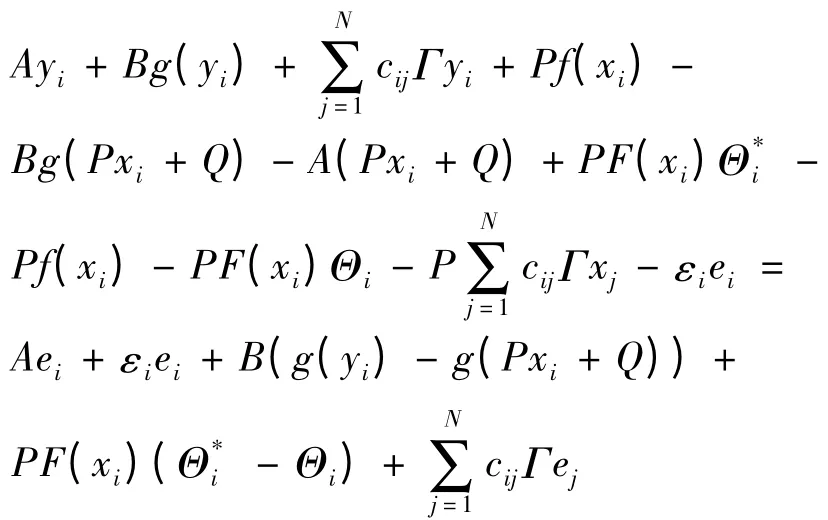
构造Lyapunov函数

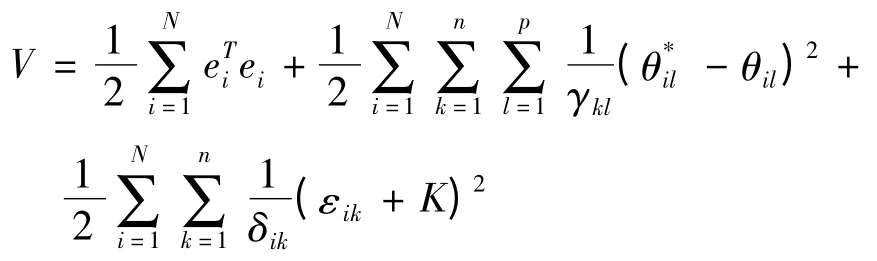
其中K是大的正常数，则

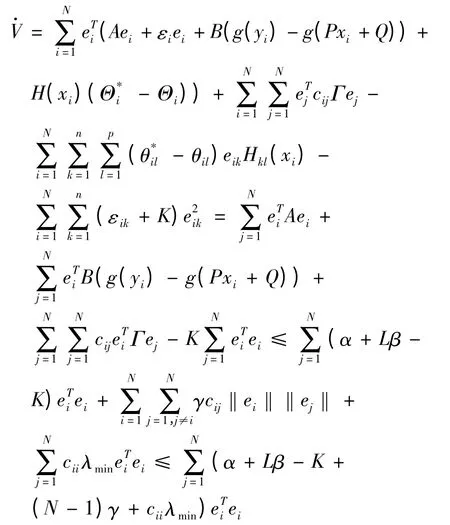
其中λmin为矩阵(Γ+ΓT)/2的最小本征值.如果常数K充分大就有≤0.根据Lyapunov稳定性理论［23］和LaSalle不变性原理［24］，网络(1)和(2)的任何轨迹(xi(t)，yi(t)，，εi)(i=1，2，…，N)最终收敛于不变集其中分别为常矢量和常矩阵.以下证明

事实上，根据Ei中的轨道的不变性，有H(xi)(-Θi)=0，即

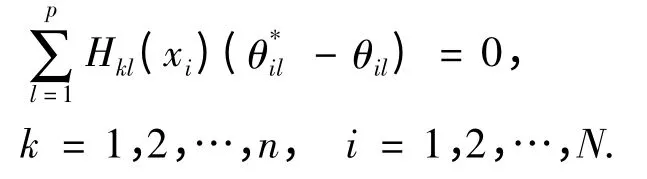
根据下面的命题，未知参数会被追踪识别，定理证明完毕.

命题 (ⅰ)对于任意给定的k∈{1，2，…，n}，若p=1，且

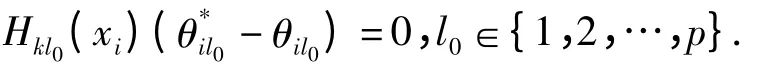
则只要同步流型yi=φ(xi)使Hkl0(xi)≠0，就有

(ⅱ)若p≥2，则只要同步流形yi=φ(xi)使{Hkls(xi)，ls∈{1，2，…，p}}线性无关，则也有成立.

3 数值仿真

考虑驱动动力学复杂网络的节点为Lü系统:

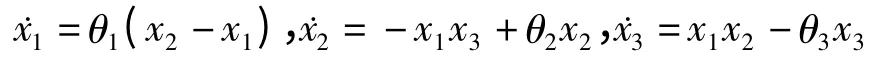
改写成驱动网络(1)中的系统形式为

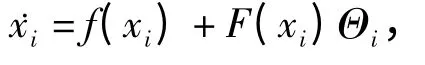
其中

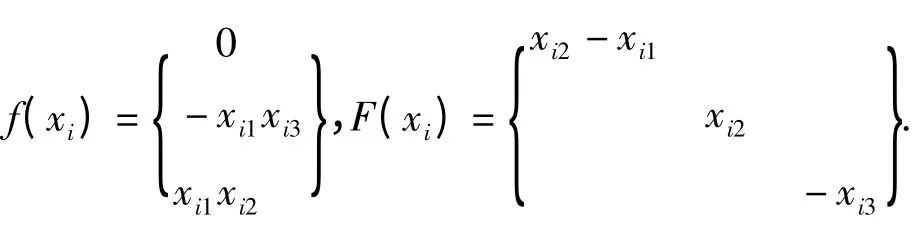
响应动力学复杂网络的节点为Rössler系统为:

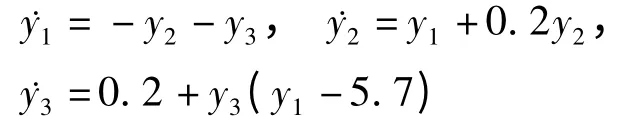
改写成网络(2)中的系统形式为

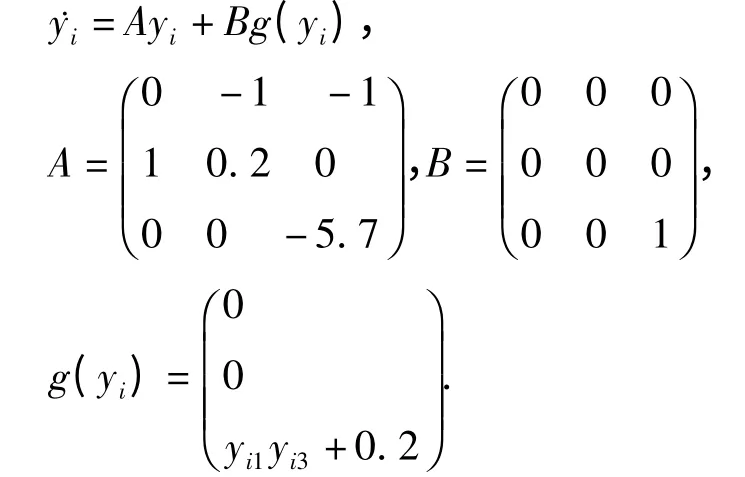
取N=5，耦合矩阵C=(cij)5×5及内耦合矩阵Γ分别为

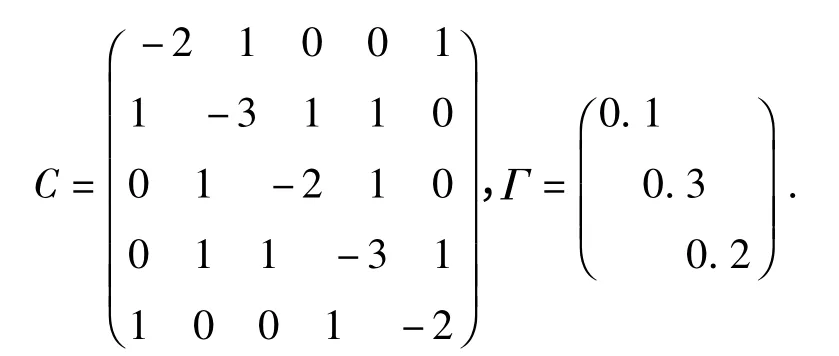
则对应(1)(2)形式的驱动响应网络分别为:

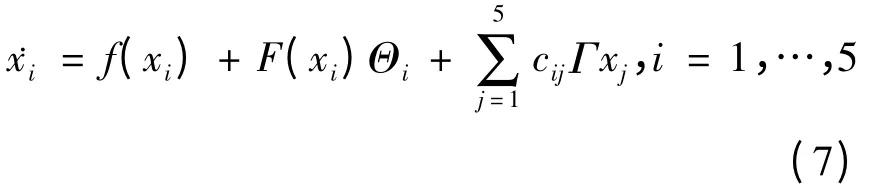
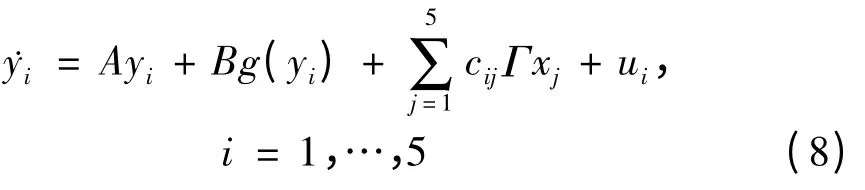
有‖A‖=5.7897，‖B‖=1，‖Γ‖=0.1，满足定理条件(i).Lü系统和Rössler系统满足定理条(ii)［26］.在仿真中取线性广义同步中的P=diag(1，-2，3)，Q=［0 0 0］T，误差ei1=yi1-xi1，ei2=yi2+2xi1，ei3=yi3-3xi3，(i=1，…，5).根据上面的定理，自适应控制器ui由(4)式给出，反馈控制和未知参数识别由如下公式给出:

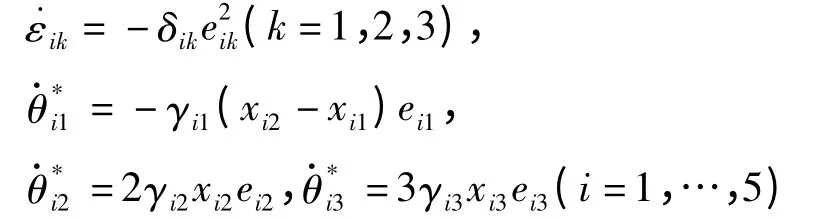
其中

目标参数为Φi=(36，20，3)，选取初值

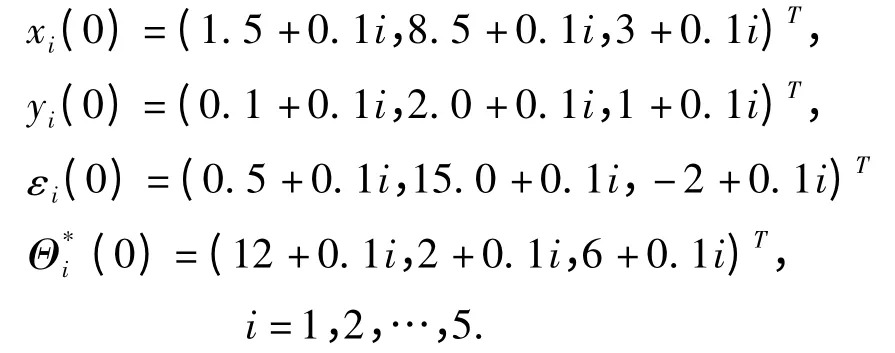
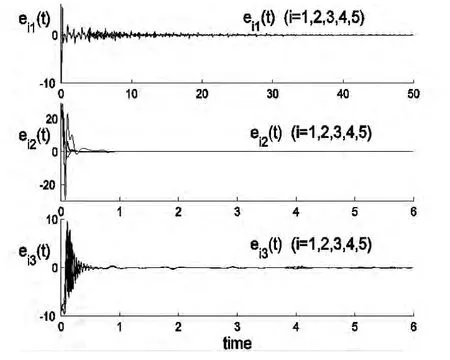
图1 驱动网络(7)和响应网络(8)之间的线性广义同步误差Fig.1 The time evolution of the linear generalized synchronization errors between drive network(7)and response network(8)

驱动网络(7)和响应网络(8)之间的线性广义同步误差见图1.从图1可以看到线性广义同步误差收敛于零，说明两个网络实现了线性广义同步.未知参数的追踪识别如图2，从中可看到网络(7)中的未知参数已被准确识别.在图3中，给出了驱动网络(7)和响应网络(8)中第三个节点吸引子的相空间图.

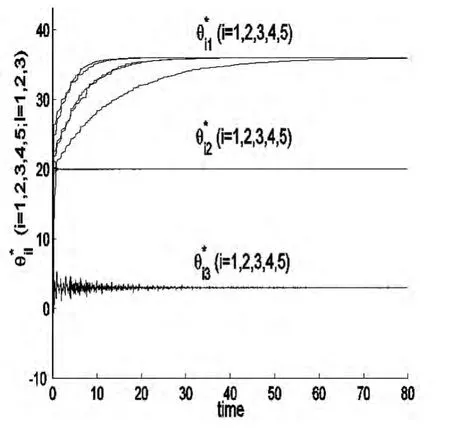
图2 和(i=1，2，…，5)的时间演化图Fig.2 The time evaluations of， and(i=1，2，…，5)

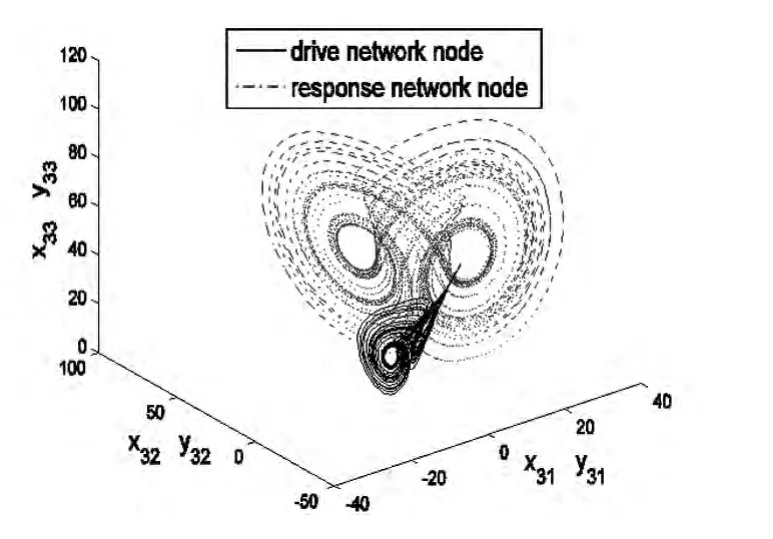
图3 网络(7)(8)中节点和的相空间线性广义同步图Fig.3 The phase graphs of linear generalized synchronization nodesandin the networks(7)(8)

4 结论

本文基于Lyapunov稳定性理论和LaSalle不变原理，针对参数未知的复杂动力学网络，设计了合适的自适应控制器不仅实现了参数未知的复杂动力学网络之间的线性广义同步，而且对网络中的未知参数进行了准确的追踪识别，设计的控制器适用于一类参数未知的复杂动力学网络.由于实际中复杂动力学网络不可避免受到如噪声和参数变动等不确定因素的影响，因此研究参数未知的不确定复杂动力学网络的同步问题有重要意义.本文不仅从理论上严格证明了控制方法的正确性，而且还通过数值仿真结果进一步验证了其有效性和可行性.

1 Huang Z X，Ruan J.Synchronization of chaotic systems by linear feedback controller.Communications in Nonlinear Science and Numberical Simulation，1998，3:27～30

2 Yu H J，Liu Y Z.Chaotic synchronization based on stability criterion of linear systems.Physics Letters A，2003，314:292～298

3 Anteneodo C，Batista A M，Viana R L.Chaos synchronization in long-range coupled map lattices.Physics Letters A，2004，326:227～233

4 Lu J H，Zhou T S，Zhang SC.Chaos synchroniization between linearly coupledchaotic systems.Chaos，Solitons＆Fractals，2002，14:529～554

5 杨涛，邵惠鹤.一类混沌系统的同步方法.物理学报，2002，51(4):742～748(Yang T，Shao H H.Synchronization for a class of chaotic systems.Acta Physica Sinica，2002，51(4):742～748(in Chinese))

6 王兴元，孟娟.超混沌系统的广义同步化.物理学报，2007，56(11):6288～6293(Wang X Y，Meng J.Generalized synchronization of hyperchaos systems.Acta Physica Sinica，2007，56(11):6288～6293(in Chinese))

7 张丽丽，雷友发.一类不同维混沌广义同步系统的构造定理及其应用.动力学与控制学报，2009，7(4):324～327(Zhang L L，Lei Y F.Construction of generalized synchronization for a kind of chaos systems of different dimensions and applications.Journal of Dynamics and Control，2009，7(4):324～327(in Chinese))

8 Rosenblum M G，Pikovsky A S，Kurths J.Phase synchronization of chaotic oscillators.Physical Review Letters，1996，76:1804～1807

9 Rosenblum M G，Pikovsky A S，Kurth J.From phase to lag synchronization in coupled chaotic oscillators.Physical Review Letters，1997，78:4193～4196

10 Xu D.Control of projective synchronization in chaotic systems.Physical Review E，2001，63:27201～27204

11 Zhang R，Yang Y Q，Xu Z Y，Manfeng Hu M F.Function projective synchronization in drive–response dynamical network.Physics Letters A，2001，374:3025–3028

12 张丽丽，雷友发.自治混沌系统普适广义投影同步理论及应用.动力学与控制学报，2013，11(2):118～121(Zhang L L，Lei Y F.Theorem of generalized projective synchronization for any autonomous chaotic systems and applications.Journal of Dynamics and Control，2013，11(2):118～121(in Chinese))

13 Rulkov N F，Sushchik M M，Tsimring L S，Abarbanel H D I.Generalized synchronization of chaos in directionally coupled chaotic systems.Physical Review E，1995，51:980～994

14 Abarbanel H D I，Rulkov N F，.Sushchik M M.Generalized synchronization of chaos:the auxiliary system approach.Physical Review E，1996，53:4528～4535

15 Femat R，Kocarev L，VanGerven L，Monsivais-Perez M E.Towards generalized synchronization of strictly different chaotic systems.Physics Letters A，2005，342:247～255

16 Meng J，Wang X Y.Generalized synchronization via nonlinear control.Chaos，2008，18(2):023108

17 Hung Y C，Huang Y T，Ho M C，Hu CK.Paths to globally generalized synchronization in scale-free networks.Physical Review E，2008，77:016202～016209

18 Xu X，Chen Z，Si G，Hu X，Luo P.A novel definition of generalized synchronization on networks and a numerical simulation.Computers＆Mathematics with Applications，2008，56(11):2789～2794

19 LüL，Li G，Guo L.Meng L，Zou JR，Yang M Generalized chaos synchronization of a weighted complex network with different nodes.Chinese Physics B，2010，19(8):080507

20 Shang Y，Chen M Y，Kurths J，Generalized synchronization of complex networks.Physical Review E，2009，80:027201～027204

21 Khan M A.Generalized synchronization of lorenz chaotic system with star network.International Journal of Applied Mathematical Research，2012，1(4):409～421

22 Sun M，Zeng CY，Tian L X.Linear generalized synchronization between two complex networks.Commun Nonlinear Sci Numer Simulat，2010，15(8):2162～2167

23 Hale J，Lunel SV.Introduction to functional differential equations.New York:Springer，1993

24 Hassan K K.Nonlinear systems.New Jersey:Prentice Hall，2002

25 Li R H.Exponential generalized synchronization of uncertain coupled chaotic systems by adaptive control.Communications in Nonlinear Science and Numerical Simulation，2009，14:2757～2764

26 Chen Y H，Chang CH.Impulsive synchronization of Lipschitz chaotic systems.Chaos，Solitons＆Fractals，2009，40:1221～1228