交换半环上上三角矩阵半环的自同构

黄惠玲

（福建船政交通职业学院公共教学部，福建福州350007）

交换半环上上三角矩阵半环的自同构

黄惠玲

（福建船政交通职业学院公共教学部，福建福州350007）

设R为任意含单位元的半环，Tn（R）为半环R上的上三角矩阵半环。利用矩阵的一些性质，得出了半环Tn（R）上的任一半环自同构Φ的一些结论，即（1）当n＝1时，Φ为半环Tn（R）的一个半环自同构。（2）当n≥2时，存在半环Tn（R）的内自同构φz，半环自同构μg使Φ＝φzμg。

半环；矩阵半环；自同构

1 引言和预备知识

设R是含有恒等元1的半环。Tn（R）是R上的n阶上三角矩阵构成的矩阵半环。当R是一个交换环时，谢乐平，曹佑安研究了上三角矩阵环的自同构［1］。本文在上述基础上进一步讨论交换半环中的情况，所得结果推广了文［1］的结论。

关于半环、半环上的自同构，半环R上的反元等基本概念可参见文献［2］、［3］或［4］。

定义1设R是半环，R上所有n阶方阵组成的集合关于矩阵的加法和乘法构成一个半环，称为半环R上的矩阵半环。记为Mn（R）。

设R*是R的单位组成的群。Tn（R）表示半环R上所有上三角矩阵组成之集，则不难验证Tn（R）为Mn（R）的的子半环，称为半环R上的上三角矩阵半环。

设Epq表示第p行第q列交叉处的元素为1，而其余元素全为0的n阶方阵。E是n阶单位矩阵。为了方便起见，我们约定在一个矩阵的表达式∑aij中，下标i可以小于1，j可以大于n，并且如果i＜1或j＞n，那么系数aij规定为0。

AutTn（R）表示半环Tn（R）的自同构群。设Mr，且r≥n时，Mr＝0。设Φ是半环Tn（R）的任一自同构，并且设

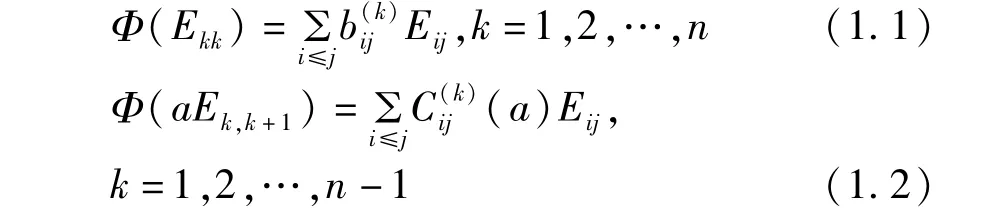
定义2 设X为Tn（R）中任意的可逆矩阵。半环Tn（R）的自同构φX：YXYX－1称为内自同构。

定义3设g是半环R的一个自同构。映射μg：Tn（R）→Tn（R），j是 半环Tn（R）的一个自同构，称为半环自同构。

本文中若无特别声明，半环R均指含有恒等元1的交换半环。

2 主要结果

引理1对任意1≤r≤n－1，有Φ（Mr）＝Mr。

证明先证Φ（Mr）⊆Mr。

因为∀a∈R，当m－l≥r时，我们有

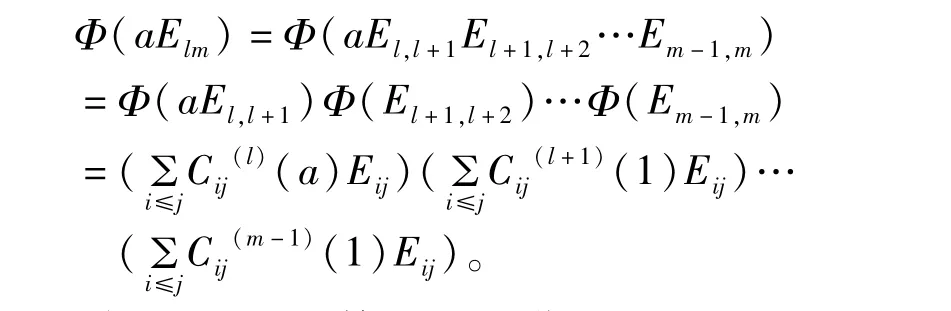
则Φ（aElm）的第（i，j）—位置（这里j－i＜r）的元素是

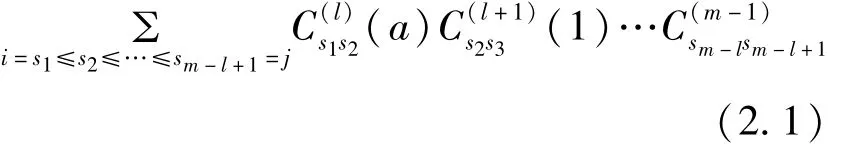
这里整数S1，S2，…Sm－l＋1位于［i，j］之中。因为j－i＜r，所以［i，j］中只含有r个不同的整数。又因为m－l≥r，则m－l＋1≥r＋1，因此必存在t（1≤t≤m－l）使得St＝St＋1。

因此我们有C（k）StSt＋1（d）＝C（k）StSt（d）＝0，这里当t＝1时，d＝a；当t＞1时，d＝1。

因此Φ（Mr）⊆Mr，又因为Φ是可逆的，所以Φ（Mr）＝Mr。证毕。

引理2设Φ是半环Tn（R）的任一自同构，且

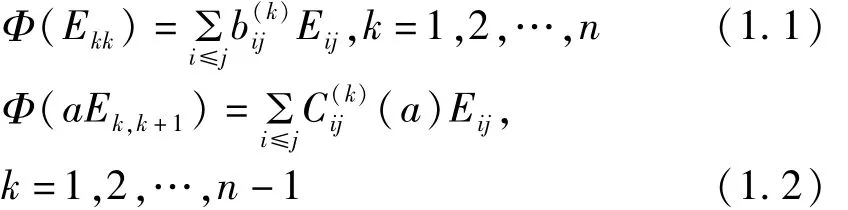
则当n≥2时，有

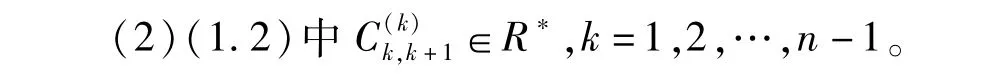
证明由引理1，我们有Φ（Mn－1）＝Mn－1，因此存在a∈R使得Φ（aE1n）＝E1n。

因为E12·E23…Ek－1，k·Ek，k＋1…En－2，n－1· aEn－1，n＝aE1n，两边用Φ作用可得

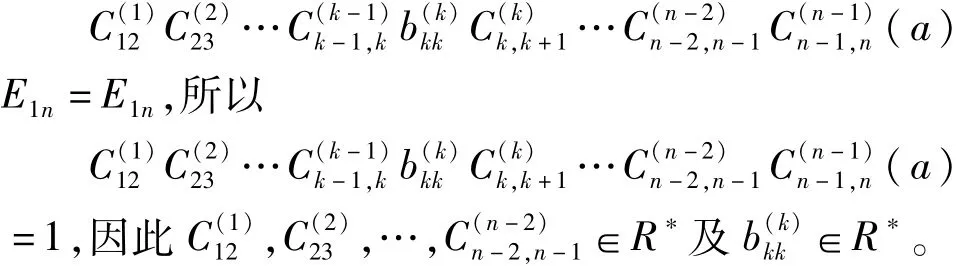
同理，因为aE12E23…Ek－1，kEk，kEk，k＋1…En－2，n－1En－1，n＝aE1n，两边用Φ作用可得∈R*，因此结论（2）成立。

引理3设Φ是半环Tn（R）任一自同构，且Φ（Ekk）＝Eij（k＝1，2，…，n），那么

（1）当i＞k或j＜k时，b（k）ij＝0，即

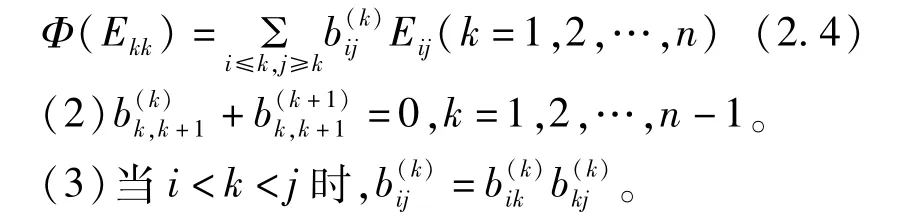
证明（1）设q＝j－i，则因为i＞k或j＜k，当q＝0，即i＝j时，由引理2的（1）可得＝0，结论成立。

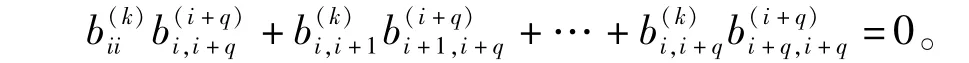
（2）因为EkkEk＋1，k＋1＝0，用Φ作用于等式两边，比较所得结果两边的（k，k＋1）－位置元素，可得由引理2的（1）可得，所以，即结论（2）成立。

引理4设为矩阵Φ（Ekk）的元素。设

证明设Y＝

显然XY对角线上的元素皆为1，而（i，j）－位置元素（i＜j）为

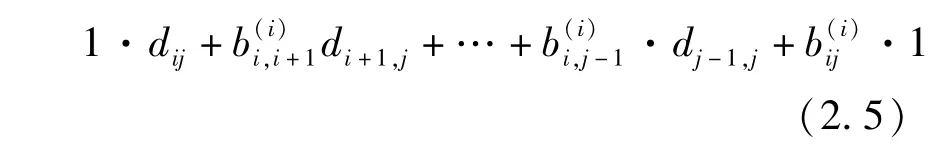
我们只要证（2.5）式为0即可。

当j＝i＋1时，因为dij＋＝0，（2.5）式即为dij＋＝0。

当j＞i＋1时，不妨设i＜m＜j，下面证明

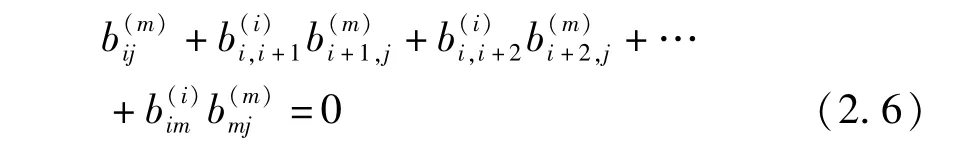
因为EiiEmm＝0，用Φ作用于等式两边，比较所得结果两边的（i，j）－位置元素有

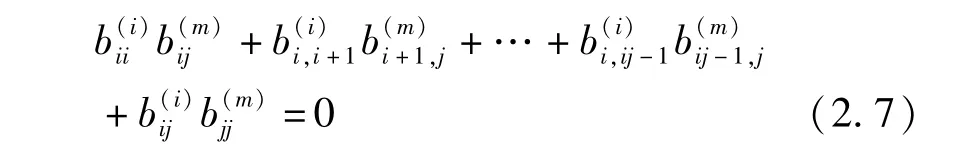
由（2.6）式可知

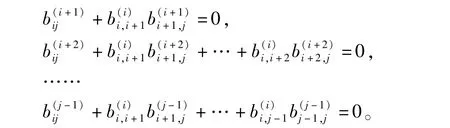
把上面等式的左边都加到（2.5）式，并由dij＋可得

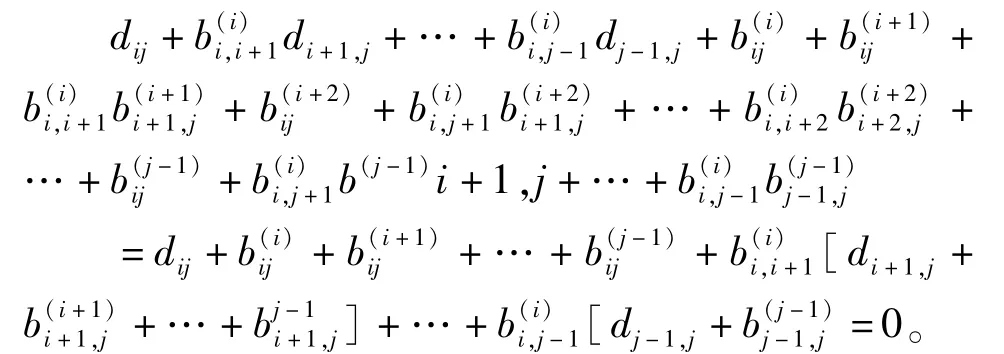
引理5设X为引理4中的矩阵，φX为半环Tn（R）的内自同构，那么Φ（Ekk）＝Ekk，k＝1，…，n。

证明首先证明

观察XΦ（Ekk）的（i，j）－位置元素hij，1≤i≤j≤n，通过计算可得hij＝0，i＞k或j＜k。

对于i＜k且j≥k的情形，因为X（Φ（Ekk））2＝XΦ（Ekk），因此hij就是该等式左边的（i，j）－位置元素，即为

又因为EiiEkk＝0，用Φ作用等式两边，比较所得结果两边的（i，j）－位置元素，可得

下面证明XΦ（Ekk）X－1＝Ekk。

显然XΦ（Ekk）X－1的（i，j）－位置元素（i≠k）是0，且（k，k）－位置元素是1，利用引理4XΦ（Ekk）X－1的（k，j）－位置元素，由引理4证明中的（2.6）式可得上式值为0，因此结论成立。

定理设R是一个任意含单位元的交换半环，Tn（R）表示R上n阶上三角矩阵半环，Φ是半环Tn（R）的任一个自同构，那么

（1）当n＝1时，Φ为半环Tn（R）的一个半环自同构。

（2）当n≥2时，存在半环Tn（R）的内自同构φz，半环自同构μg使Φ＝φzμg。

证明（1）当n＝1时，结果显然。

（2）由引理5可得

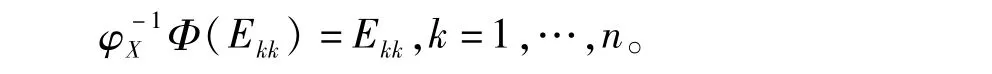
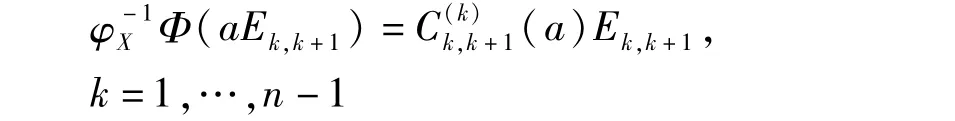
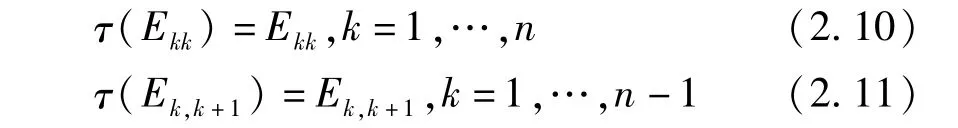
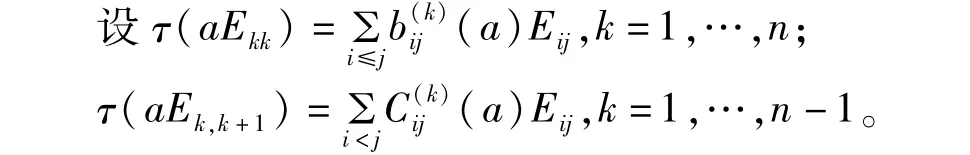
用τ分别作用于等式Ekk·aEkk＝aEkk和等式aEkk·Ekk＝aEkk两边，可得

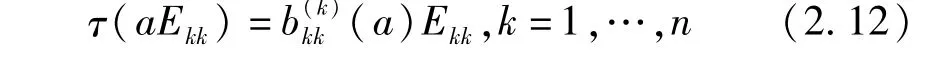
同理，因为Ekk·aEk，k＋1＝aEk，k＋1，aEk，k＋1· Ek＋1，k＋1＝aEk，k＋1，所以用τ分别作用于上面两等式的两边可得

由（2.10）（2.11）可得（1.12）（1.13）两式中（1）＝1（1）＝1。

设gk（a）＝（a），k＝1，…，n。因为aEii· Ei，i＋1＝Ei，i＋1·aEi＋1，i＋1，用τ作用等式两边得

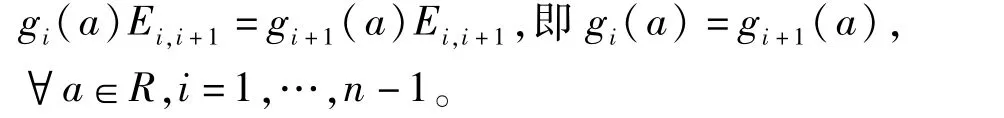
不妨设g（a）＝g1（a）＝…＝gn（a），∀a∈R。

因为Ekk·aEk，k＋1＝aEkkEk，k＋1，用τ作用于等式两边得（a）＝g（a），∀a∈R，k＝1，…，n－1。因此（2.12）（2.13）两式为显然g：R→R是一个双射。用τ作用等式（a＋b）Ekk＝aEkk＋bEkk两边得

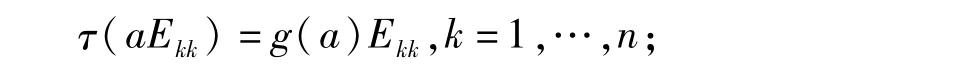
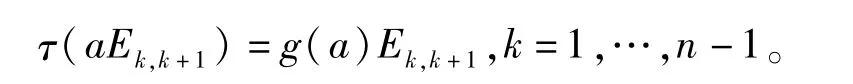
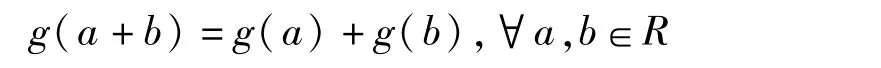
再用τ作用于等式（ab）Ekk＝aEkk·bEkk两边得

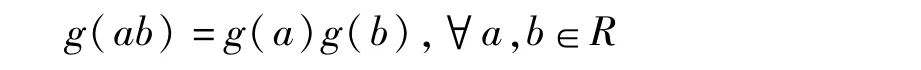
因此g是半环R的一个自同构，从而给出Tn（R）的一个半环自同构μg，显然Φ平凡地作用在下列矩阵上：

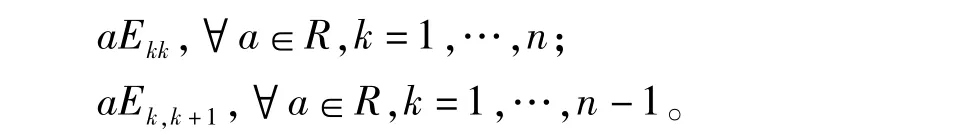
而这些矩阵构成半环Tn（R）的一组生成元。因此是Tn（R）的恒等自同构，即Φ＝φzμg。证毕。

［1］谢乐平，曹佑安.交换环上上三角矩阵环的自同构［J］.湘潭大学自然科学学报，2002，24（4）：1－5.

［2］Jacobson N.Basic Algebra I［M］.New York：W.H.Freeman and Company，1985.

［3］Golan J S.Semirings and their Applications［M］.London：Kluwer Academic Publisher，1999.

［4］陈陪慈.半环理论与语言和自动机［M］.江西：江西高校出版社，1993.

［责任编辑 毕 伟］

Automorphism s of the Upper Triangular M atrx Sem iring over Commutative Sem irings

HUANG Hui-ling
（Basic Department，Fujian Chuanzheng Communications College，Fuzhou 350007，China）

Let R be a commutative semiring with identily.In this paper，we give some characterizations of the automorphisms of the upper triangularmatrix semiring Tn（R）over commutative semirings.

semiring；matrice semiring；automorphism

O152.3

A

1004－602X（2014）03－0017－04

10.13876/J.cnki.ydnse.2014.03.017

2014-04-14

福建省自然科学基金资助项目（2008J0186）

黄惠玲（1976—），女，福建平和人，福建船政交通职业学院讲师。