M矩阵与非负矩阵特征值界的研究

李艳艳

(文山学院 数学学院，云南 文山 663000)

1 预备知识

非负矩阵，M矩阵是矩阵理论分析中非常重要的两类矩阵，并且应用于许多领域。近年来关于它们研究的一个重点是非负矩阵的Hadamard积A◦B，M矩阵的Fan积A*B的特征值界的估计。自从2004年以来陈省生，黄荣，李厚彪，李耀堂，刘庆兵，李艳艳，刘新等许多学者给出了它们特征值的上界或下界的估计式。由于不同的估计式所依据的理论知识与技巧，方法不同，所以它们之间从理论上往往没有可比性，也就是说只能借助具体的例子说明各自的优缺点。本文利用相似矩阵具有相同特征值的性质从而构造它们的相似矩阵的角度继续研究该类问题。

下面首先给出本文要用到的一些定义和引理

定义1［1］如果矩阵 A=(aij)m×n的所有元素aij≥0，则称矩阵A为非负矩阵，记作A≥0;若 aij＞0，则称矩阵A为正矩阵。

定义2［1］如果矩阵A=(aij)n×n的非主对角元素 aij≤0，i，j∈N，i≠j，则称 A 为 Z 矩阵;若 A 为 Z矩阵且A－1≥0，则A为非奇异M矩阵。q(A)表示非奇异M矩阵A的最小特征值。

定义 3［1］设 A=(aij)∈Cm×n，B=(bij)∈Cm×n，A◦B表示A和B的对应元素相乘而成的

m×n矩阵

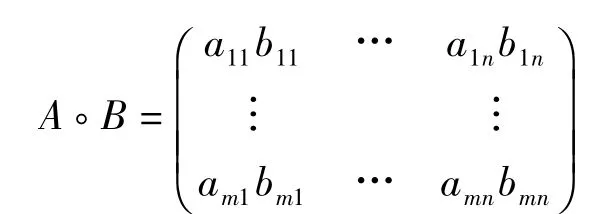
A◦B称为A和B的Hadamard积。

定义 4［1］设 A=(aij)∈Cm×n，B=Cm×n，设A*B=(Cij)，

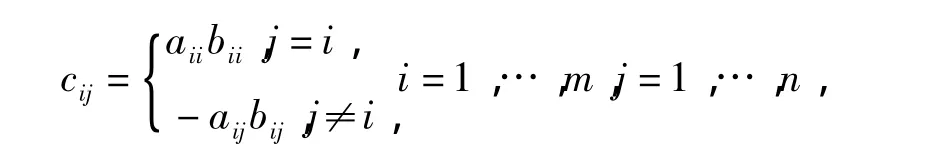
称为A和B的Fan积。

定义5［1］设A=(aij)是非奇异M矩阵，令Z(A)=A －D(A)，D(A)=diag(aij)且 aij＞0，则 JA=－D－1Z(A)≥0，称为非奇异M矩阵的迭代矩阵。

引理 1［2］设 A=(aij∈Rn×n)，用 σ(A)表示 A的谱(A的特征值的集合)

1)若A是非负矩阵，则由Perron－Frobenius定理知，A的谱半径ρ(A)∈σ(A);

2)若A是M矩阵，τ(A)是A的最小特征值，则τ(A)∈σ(A)。

引理 2［2］A=(aij)∈Rn×n，则

1)若A是不可约非负矩阵，则存在正向量u使Au=ρ(A)u，其中u称为A的右Perron特征向量。

2)若A是不可约非奇异M矩阵，则存在正向量v使Av=τ(A)v，其中v称为A的右Perron特征向量。

定义 6［2］设 A=(aij)∈Rn×n，如果存在 n × n置换矩阵P使

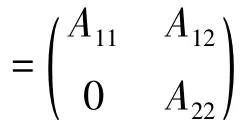
引理 3［3］设 A=(aij)∈Cn×n，x1，x2，…xn是一组正实数。则A的所有特征值包含在复平面C的如下区域中:

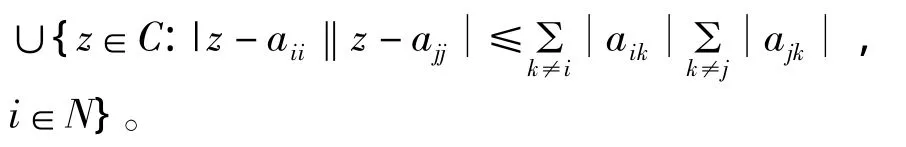
引理 4［3］设 A=(aij)∈Rn×n是非负矩阵，则

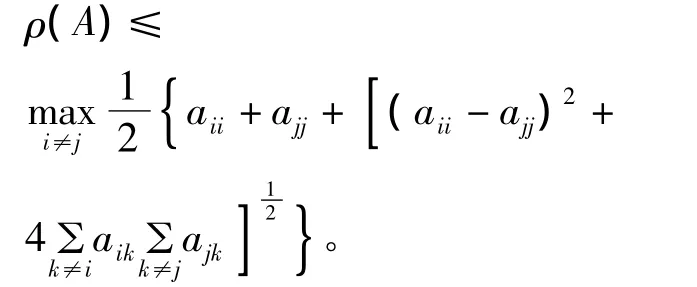
另一方面，若A不可约，则

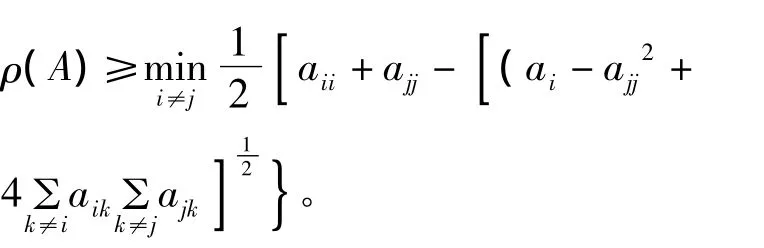
2 主要结果

下面分三部分给出本文研究的主要问题。

非奇异M矩阵的迭代矩阵JA的谱半径ρ(JA)的上界。

定理1 设A=(aij)∈Rn×n是非奇异M矩阵，x1是正实数，则

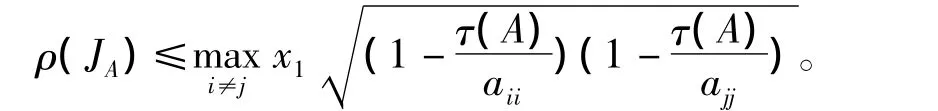
证明:定义 D=diag(d1，d2，…，dn)为正对角矩阵，则D－1AD与D相似，即它们具有相同的特征值，ρ(JA)= ρ(JD－1AD)。

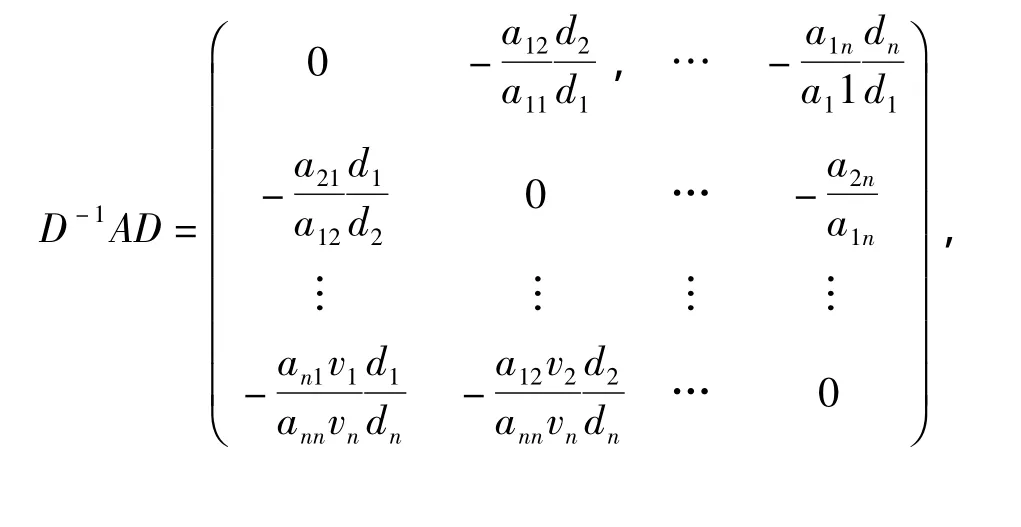
因为A是非奇异M矩阵，由引理2知存在正向量 v使 Av=τ(A)v且 aii－τ(A)＞0，∀i∈N，

由引理4知

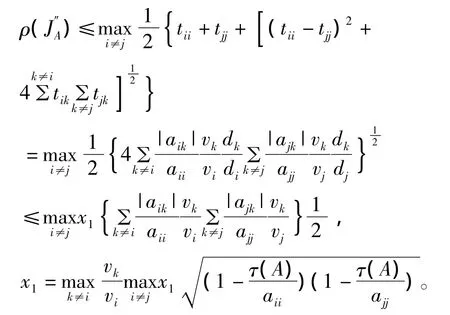
M矩阵的Fan积最小特征值的下界。

引理5［2］设A，B是非奇异 M － 矩阵，D，E是正对角矩阵则，

D(A*B)E=(DAE)*B=(DA)*(BE)=(AE)*(DB)=A*(DBE)。

定理2 设A，B是非奇异M－矩阵，m＞0则

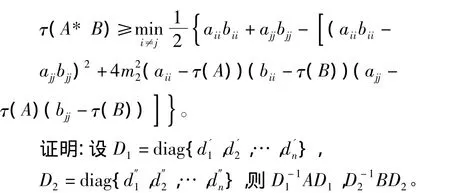
则存在正向量U和V使得

令 U=diag(u1，u2，…，un)，V=diag(v1，v2，…，vn)，则U，V是非奇异对角矩阵。

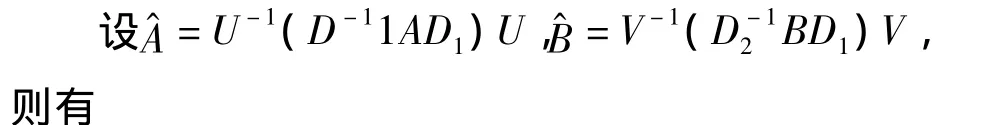
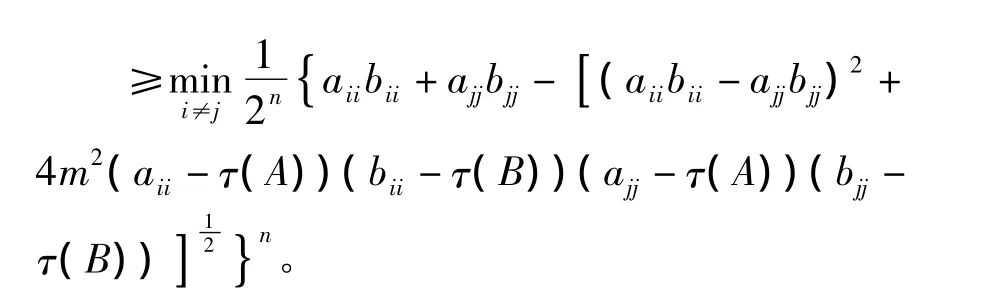
非负矩阵A与B的Hadamard积A◦B的谱半径的上界。

类似于定理2的证明可得定理3。

定理3 设A，B是非负矩阵，m＞0则

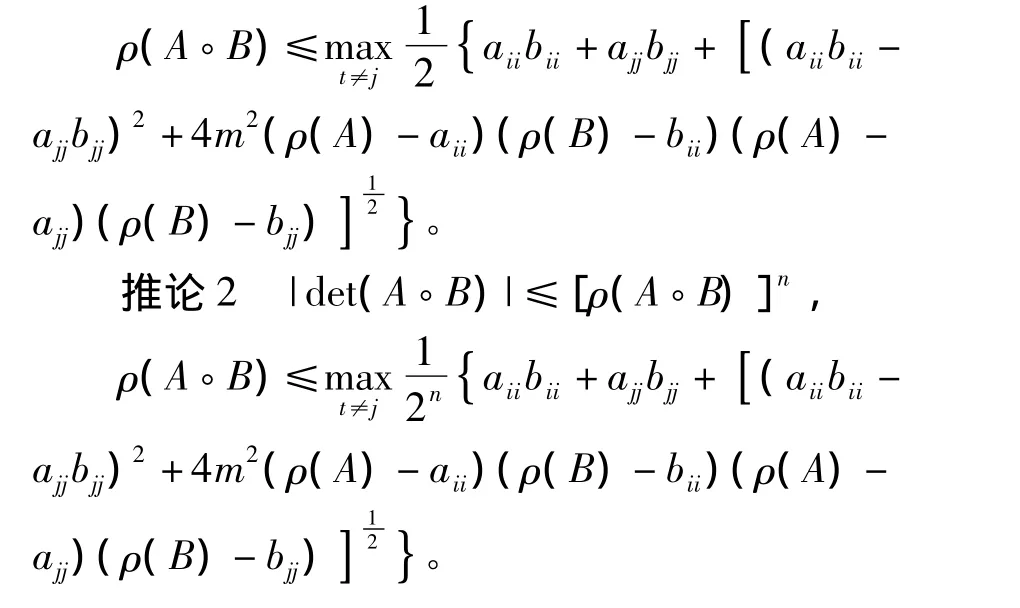
3 数值算例

应用参考文献［4］中定理4得 τ(A*B)≥0.7655。应用本文定理2得τ(A*B)≥0.8729，事实上 τ(A*B)=0.8819。

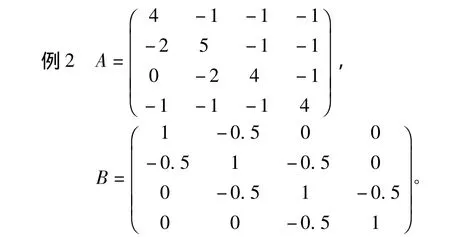
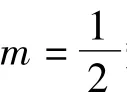
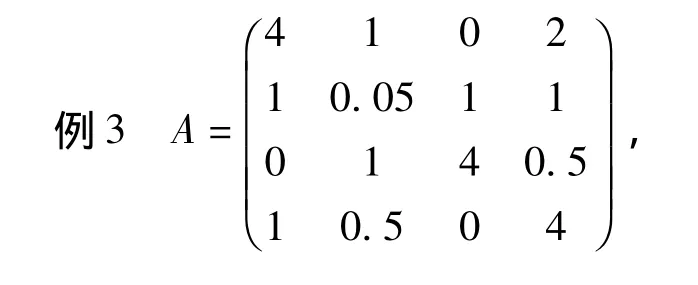
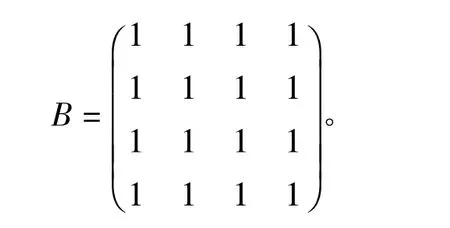
应用参考文献［4］中定理2得 ρ(A◦B)=11.6438，应用定理2得ρ(A◦B)≤6.7340，事实上ρ(A ◦B)=5.7339。

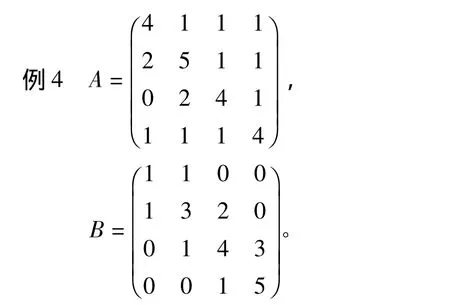
应用参考文献［4］中定理2ρ(A◦B)≥25.3634。应用定理2得ρ(A◦B)≤21.9275，事实上ρ(A◦B)=20.7439。

数值算例说明本文所得结果提高了现有的估计式，而且本文推导估计式的这种方法以前的学者所没有用到的。

［1］黄廷祝，杨传胜.特殊矩阵分析及应用［M］.北京:科学出版社，2007.

［2］陈景良，陈向晖.特殊矩阵［M］.北京:清华大学出版社，2000.

［3］李艳艳，李耀堂.矩阵Hadamard积和Fan积的特征值界的估计［J］.云南大学学报(自然科学版)，2010，32(2):125－129.

［4］LIU Qing－ bing，CHEN Guo－ liang，ZHAO Lin － lin．Some new bounds on the spectral radius of matrices［J］．Linear Algebra and its Applications，2009，432:936 －948．

［5］刘新，杨晓英.矩阵Hadamard积最小特征值的新下界［J］.重庆师范大学学报(自然科学版)，2013，30(2):53－55.