基于生物地理优化算法的数值积分方法实验
2014-02-09唐权华
张 晶, 唐权华, 贾 璐
(1. 四川宜宾学院 图书馆, 四川 宜宾 644007; 2. 江西师范大学 软件学院,江西 南昌 330022;3. 西南交通大学 峨嵋校区, 四川 峨嵋 614202)
0 引 言
数值积分计算方法是连接工程问题与科学计算的桥梁;是便于应用计算机解决实际工程问题的具体算法。在数值积分计算中,常用的有梯形法、Simpson法等很多传统计算方法[1-3]。这些传统的计算方法精度较低,可利用非数值优化方法来求解数值积分,例如粒子群算法[4]。数值积分计算方法通过不等距节点积分方法,在积分区间内任意选取一定节点,通过粒子群算法(Particle Swarm Optimization,PSO)优化这些节点,得到了比较精确的积分结果。该方法好于梯形法和Simpson法,但PSO算法收敛速度慢、收敛精度低[5-6],在一定程度也会降低数值积分的精度。因此,有必要采用更有效的智能优化算法来求解数值积分问题。
Simon依据生物种群在栖息地的分布、迁移、变异和灭绝的规律,首次提出了生物地理优化算法(Biogeography-Based Optimization,BBO)[7]。与PSO相比,BBO具有简单方便、参数少、收敛速度快、收索精度高的特点,已经被应用到很多工程技术问题[8-15]。因此,本文利用BBO算法求解数值积分问题,并与传统的计算方法和PSO算法进行对比。
1 BBO的基本原理
BBO算法通过群体中相邻个体的迁徙和特殊个体的变异来寻找全局最优解[7-10]。在BBO算法中,生物种群生活在不同的栖息地 (Habitat,H),每个栖息地根据物种种类的多少决定该栖息地的适应性特性。
定义1适合物种居住的栖息地有较高的栖息地适应性指数(Habitat Suitability Index,HSI):H→R,R表示实数,表示对解集适应度的评价[9-10]。在优化问题中,若选择HIS适应度函数量化,则好的解集具有高HIS的栖息地;反之则具有低HSI的栖息地。
定义2与HSI有关的特性如雨量、温度等,用适合指数变量(Suitability Index Variables,SIV)描述:SIV∈C,C为整数集,表示构成H的元素。若存在H∈SIVn,则由n个SIV构成的矢量表示优化问题的可能解[10]。
BBO算法的核心操作是物种的迁徙和变异。每个栖息地都有自己的迁入率和迁出率,通过栖息地之间的迁移,栖息地之间可以直接分享适应性特性,个别栖息地物种的变异能进一步提升该栖息地的适应性。设栖息地具有物种种类S的概率为PS,在t到t+Δt时间内,概率PS改变为PS(t+Δt),则有:
PS(t+Δt)=PS(t)(1-(λS+μS)Δt)+
PS-1(t)λS-1Δ(t)+PS+1(t)μS+1Δ(t)
(1)
式中:λS和μS分别表示该栖息地物种种类为S时的物种迁入率和迁出率。为了使式(1)成立,即使得t+Δt内有S类物种,必须满足相关条件[11],当Δt足够小,式(1)对时间取极限,得:
PS=-(λS+μS)PS+λS-1PS-1+μS+1PS+1
(2)
设物种种群最大数为Smax,最大迁入率为E,最大迁出率为I,并令E=I。物种迁移模型如图1所示。从图中可以看出,在迁移率为E时,μS为0,物种种类为0;当λS=μS时,物种种类达到稳定状态S0;当λS=0,uS=E时,物种种类达到最大值Smax。因此,可以得到:
迁移算子采用离散方式,即将邻近栖息地Hj中的SIV迁移给Hi中的SIV:
Hi(SIV)=Hj(SIV)
(6)
设最大变异率为mmax,栖息地个数为n,则基于线

图1 栖息地物种迁移模型
性的变异率模型如下:
m(S)=mmax(1-PS/Pmax)
(7)
式中,Pmax=arg maxPi,i=1,2,…,n。
2 BBO求解数值积分
依据不等距节点原理,BBO求解数值积分具体算法如下:
(1) 初始化BBO算法参数。首先给出栖息地数量n、栖息地最大种群数Smax、最大迁入率E和最大迁出率I,最大变异率mmax,优化问题的维度D等参数,然后随机初始化每个栖息地的HIV向量xi(i=1,2,…,n),每个HIV向量对应于优化问题的一个可能解。
(2) 计算栖息地的适应度f(xi)。根据文献[4],将xi置于积分区间的左右端点之间,并按照升序排列,积分区间总共有D+2个节点和D+1小段。先计算D+2个节点相邻节点之间的距离dj(j=1,2,…,D),再计算D+2个节点对应的函数值和D+1个小段中间节点的函数值。对比每小段左端点、中间节点和右端点积分函数值,函数值最小的记为wj,最大的记为Wj(j=1,2,…,D+1),从而得到第i个栖息地的适应度为
(8)
(3) 计算栖息地的迁入率和变异率,重新计算适应度f(xi)。计算栖息地i对应的物种种类Si,迁入率λS和迁出率uS,通过迁移和变异,重新计算栖息地i的适应度函数f(xi)。
(4) 判断是否满足停止条件,并输出数值积分结果。若达到指定精度或者迭代次数,停止迭代;否则跳转到(3),继续迭代。算法结束时,采用改进的数值积分计算公式:
(9)
式中:gj为积分区间第j个端点的积分函数值;gj+0.5为第j和j+1端点之间的积分函数值。
3 仿真实验


(a) x2
(d) sinx

(e) 1/(1+x)

(f) ex
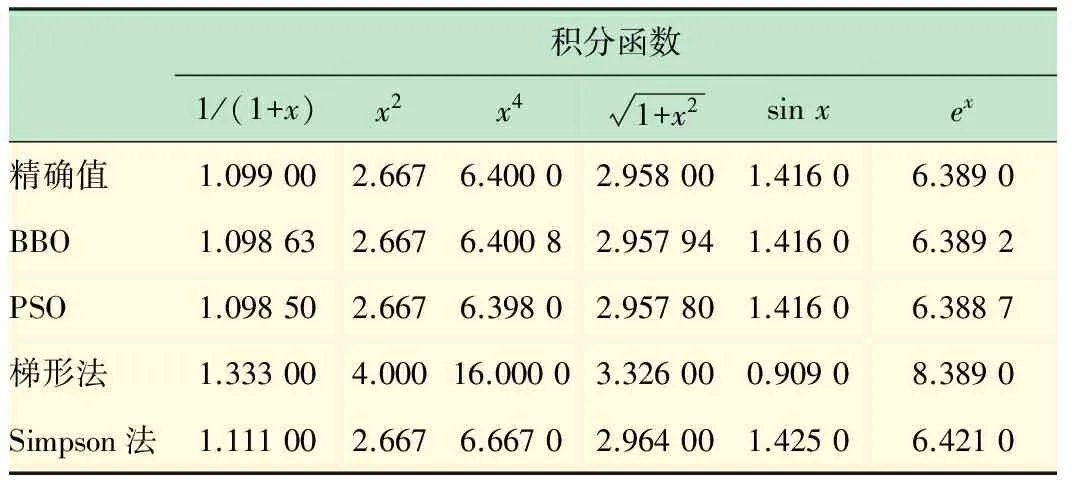
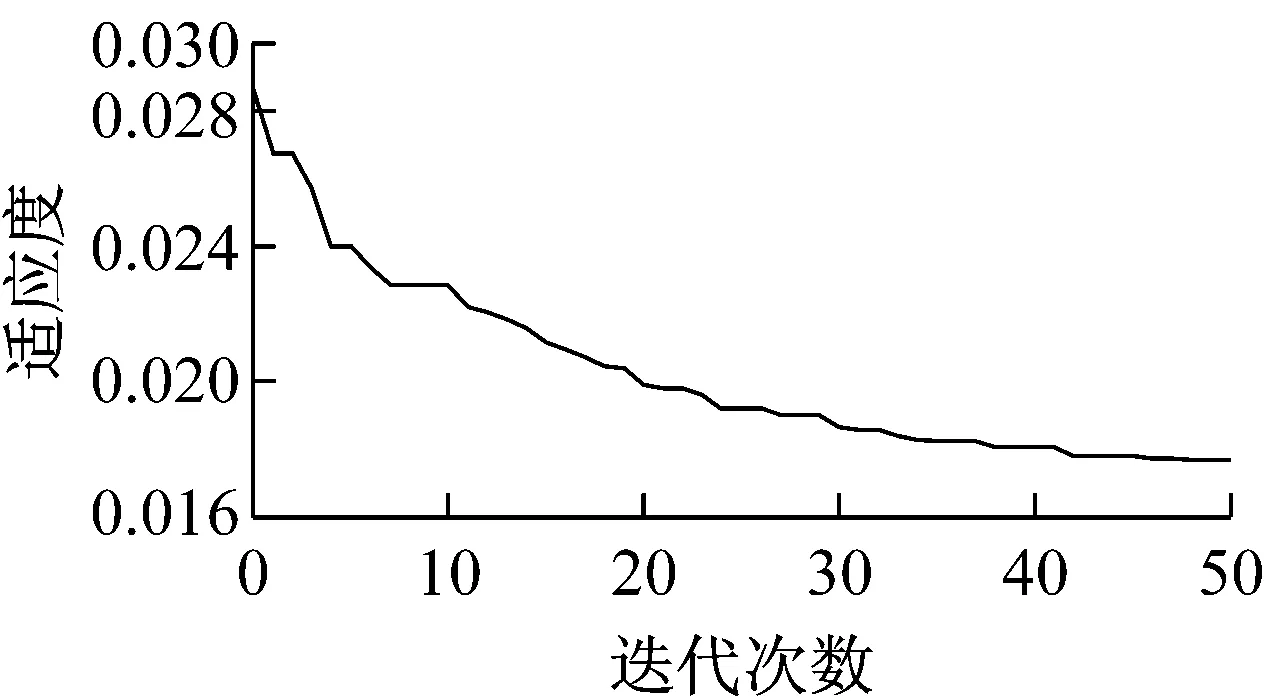
图2 积分函数的适应度变化
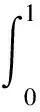

表2 基于不同积分方法的函数x/(4+x2)计算结果
图3 积分函数x/(4+x2)的适应度变化曲线
4 结 语
本文介绍了生物地理优化算法的基本原理,并给出了基于生物地理优化算法求解数值积分方法和步骤。数值积分函数算例仿真结果表明,生物地理优化算法求解数值积分精度高,自适应性强,积分结果明显好于粒子群算法、梯形法和Simpson法。
[1] 王能超.计算方法—算法设计及其Matlab实现[M ].北京:高等教育出版社, 2008:45-55.
[2] 李庆扬,王能超,易大义.数值分析[M].4版. 武汉:华中科技大学出版社,2006:86-89.
[3] 吕同富,康兆敏,方秀男.数值计算方法[M].2版. 北京:清华大学出版社,2012:258-264.
[4] 韦杏琼,周永权.基于粒子群算法的数值积分方法研究[J].微电子学与计算机,2009,26(7):118-119.
WEI Xing-qiong, ZHOU Yong-quan. Numerical Integral Method Research Based on PSO [J]. Microelectronics & Computer, 2009,26(7):118-119.
[5] Kennedy J,Eberhart R C.Particle swarm optimization[C]//Proc of the IEEE International Conference on Neural Networks.Piscataway, NJ:IEEE Service Center,1995:1942-1948.
[6] 黄少荣.粒子群优化算法综述[J].计算机工程与应用,2009,30(8):1977-1980.
HUANG Shao-rong. Survey of particle swarm optimization algorithm[J].Computer Engineering and Design, 2009,30(8):1977-1980.
[7] DAN Simon. Biogeography-based optimization[J].IEEE Transactions on Evolutionary Computation, 2008, 12(6): 702-713.
[8] 张 萍,魏 平,于鸿洋,等.基于混沌的生物地理分布优化算法[J].电子科技大学学报,2012,41(1): 65-67.
ZHANG Ping, WEI Ping, YU Hong-yang,etal. Biogeography-Based Optimization Algorithm by Using Chaotic Search[J]. Journal of University of Electronic Science and Technology of China, 2012,41(1): 65-67.
[9] 马海平,李 雪,林升东.生物地理学优化算法的迁移率模型分析[J].东南大学学报(自然科学版),2009,39(1):17-21.
MA Hai-ping, LI Xue, LIN Sheng-dong. Analysis of migration ratemodels for biogeography-based optimization[J]. Journal of Southeast University ( Natural Science Edition), 2009,39(1):17-21.
[10] 马海平,陈子栋,潘张鑫.一类基于物种迁移优化的进化算法[J].控制与决策,2009,24(11):1621-1624.
MA Hai-ping,CHEN Zi-dong, PAN Zhang-xin. Evolutionary algorithm based on species migration optimization[J]. Control and Decision, 2009,24(11):1621-1624.
[11] 张 萍,魏 平,于鸿洋.一种基于生物地理优化的快速运动估计算法[J].电子与信息学报,2011,33(5):1018-1025.
ZHANG Ping, WEI Ping, YU Hong-yang. A Biogeography-based Optimization Algorithm for Fast Motion Estimation [J]. Journal of Electronics & Information Technology, 2011,33(5):1018-1025.
[12] 王存睿,王楠楠,段晓东,等.生物地理学优化算法综述[J].计算机科学,2010,37(7):35-37.
WANG Cun-rui, WANG Nan-nan,DUAN Xiao-dong,etal. Survey of Biogeography-based Optimization[J].Computer Science, 2010,37(7):35-37.
[13] 蔡之华,龚文引,LING C X.基于进化规划的新型生物地理学优化算法研究[J].系统工程理论与实践,2010,30( 6) : 1106-1112.
CAI Zhi-hua,GONG Wen-yin,LING C X.Research on a Novel Biogeography-Based Optimization Algorithm Based on Evolutionary Programming[J].Systems Engineering-Theory & Practice,2010,30( 6) : 1106-1112.
[14] Boussad I,Chatterjee A,Siarry P,etal.Two-Stage Update Biogeography-Based Optimization Using Differential Evolution Algorithm ( DBBO)[J].Computers and Operations Research,2011,38 ( 8 ) : 1188-1198.
[15] 毕晓君,王 珏.基于混合迁移策略的生物地理学优化算法[J].模式识别与人工智能,2012,25(5):769-774.
BI Xiao-Jun,WANG Jue. Biogeography-Based Optimization Based on Hybrid Migration Strategy[J].PR & AI, 2012,25(5):769-774.
