P*(κ)线性互补问题的预估-校正内点算法

刘新泽,刘红卫,刘长河

(1.西安电子科技大学 数学系,西安 710071；2.临沧高等师范专科学校 数理系,云南 临沧 677000；3.河南科技大学 数学与统计学院,河南 洛阳 471003)

0 引 言

自从Karmarkar[1]提出线性规划的第一个内点算法后,内点算法即成为运筹学领域的研究热点之一.内点算法不仅形式简洁,而且实际执行非常有效.实践结果表明,预估-校正内点算法是求解线性规划、线性互补问题的有效方法[2-3].内点算法中大邻域算法实际计算效果较好,但理论复杂性相对较差;而小邻域算法则相反.文献[4-6]降低了大邻域算法的迭代复杂度;文献[7-8]利用预估-校正策略改进了算法的计算效果.但这些算法都是可行内点算法,即需要严格初始可行点.而在实际问题中,可能不存在严格可行点,或者不容易找到一个严格初始可行点.因此,内点算法的执行大多数采用不可行内点算法.由于不可行算法的迭代点不满足等式约束,因此算法的收敛性和复杂性分析变得十分困难.本文基于文献[5]提出的大邻域算法,给出一种求解非单调线性互补问题(LCP)的不可行二阶预估-校正算法,该算法具有O((1+κ)5/2nL)复杂度.数值实验验证了算法的有效性.

LCP的一般形式是: 求(x,s)∈n×n,使得

x≥0,s=Ax+q≥0,xs=0,

(1)

其中:A:n→n是线性算子;q∈n.如果A满足: 存在常数κ≥0,使得对任意的u∈n,都有其中:I+={i:ui(Au)i>0};I-={i:ui(Au)i<0},则称问题(1)为P*(κ)-LCP.显然,P*(κ)-LCP是单调互补问题的推广.本文记问题(1)的可行集为F={(x,s):x≥0,s≥0,s=Ax+q},解集为F*={(x*,s*)∈F: (x*)Ts*=0}.假设F*≠Ø.约定: ‖x‖(‖x‖1)表示向量x∈n的2-范数(1-范数);e=(1,…,1)T;x≥0(x>0)表示xi≥0(xi>0),i=1,2…,n,x+=max{x,0},x-=min{x,0},X=diag(x)为向量x生成的对角矩阵;xs∶=Xs.

1 算 法

假设(x*,s*)是问题(1)的任一解,则存在正数ξ>0,使得ξ≥‖(x*,s*)‖.算法的初始点为(x0,s0)=ξ(e,e).记q0=s0-Ax0.考虑问题(1)的扰动系统:

Ax-s+q=τ(q-q0),xs=μe,

(2)

其中:τ∈(0,1];μ=xTs/n.设(x(τ),s(τ))=(1-τ)(x*,s*)+τ(x0,s0),τ∈(0,1].易验证x(τ)>0,s(τ)>0是问题(1)的严格可行解.因此,对任意的(μ,τ)∈(0,∞)×(0,1],式(2)有唯一解(x(μ,τ),s(μ,τ)),这些解构成中心路径[9].当(μ,τ)→(0,0)时,中心路径的极限即为问题(1)的一个最优解.内点法用牛顿法求解方程组(2),逐渐减小μ,并使得迭代点列包含于中心路径的某个邻域内,最终得到满足允许精度的最优解.本文算法使用如下大邻域[5]:

N(β,γ)={(x,s)>0: ‖(γμe-xs)+‖1≤βγμ},

其中:γ∈(0,1/2];β∈(0,1/2].易验证: 如果(x,s)∈N(β,γ),则xs≥(1-β)γμe.

设(x,s)∈N(β,γ),τ∈(0,1].首先计算预估方向(Δxa,Δsa):

AΔxa-Δsa=(1-σ)τ(q0-q),sΔxa+xΔsa=(γμe-xs)-+n(γμe-xs)+,

(3)

其中σ∈(0,γ).其次计算校正方向:

AΔxc-Δsc=0,sΔxc+xΔsc=-ΔxaΔsa;

(4)

新迭代点:

其中α∈(0,1]是使得xTs和‖Ax-s+q‖能充分下降并使(x,s)∈N(β,γ)成立的最大步长.设

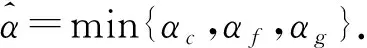
算法1输入:ε>0,γ∈(0,1/2],σ∈(0,γ),β∈(0,1/4].初始点(x0,s0)∈N(β,γ),τ0=1.令k=0.当(xk)Tsk>ε时执行如下步骤:

1) 解式(3)得到预估方向(Δxa,Δsa);

2) 解式(4)得到校正方向(Δxc,Δsc);

注1记残余为rk=Axk-sk+q,利用式(6),(7)可得

显然,(xk)Tsk→0⟹rk→0.

2 收敛性分析

引理1[2]如果LCP是P*(κ),则对任意的(x,s)>0和a,b∈n,系统:Au-v=b,su+xv=a有唯一解(u,v),并且满足:其中:

引理2设(x*,s*)∈F*,并且序列(x,s,τ)由算法1产生,则有估计:

τ((x0-x*)Ts+(s0-s*)Tx)≤(2+8κ)nμ.

证明: 显然A(τ(x0-x*)+x*-x)-(τ(s0-s*)+s*-s)=0.再注意到xTs≥τ(x0)Ts0,利用文献[2]中引理3.5的证明方法易证结论成立.

证明：因为Ax*-s*=q,Ax0-s0=q0,则A(x0-x*)-(s0-s*)=q0-q.因此,对于z=(x,s),有

又由于

其中最后一个不等式由引理2和(x,s)∈N(β,γ)可得.同理,有

因此结论成立.

引理4设(x,s)∈N(β,γ),(Δxa,Δsa)是式(3)的解,则存在常数C>1,使得:

证明：易知〈(γμe-xs)-,(γμe-xs)+〉=0.将引理1用于式(3),可得

记I={i:xisi≥γμ},可得

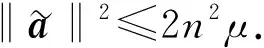
利用‖(Δxa,Δsa)‖z的定义,可知结论成立.证毕.

在上面证明中使用同一常数C≥1,后面的论述中将采用同一处理方法.

引理5设(x,s)∈N(β,γ),(Δxc,Δsc)是式(4)的解,则:

证明：由式(4)知,D-1Δxc+DΔsc=(xs)-1/2(-ΔxaΔsa).由引理1和引理4的证明,可得

推论1设(x,s)∈N(β,γ),则存在常数C≥1,使得:

1) |(Δxa)TΔsc|/n≤‖D-1Δxa‖‖DΔsc‖≤C(1+κ)5n3μ;

2) |(Δxc)TΔsa|/n≤‖D-1Δxc‖‖DΔsa‖≤C(1+κ)5n3μ;

3) |(Δxc)TΔsc|/n≤‖D-1Δxc‖‖DΔsc‖≤C(1+κ)7n4μ.

证明：仅证1),其他类似可证.首先,有

|(Δxa)TΔsc|/n=|eT(ΔxaΔsc)|/n≤‖e‖‖ΔxaΔsc‖/n≤‖ΔxaΔsc‖.

其次,由引理4和引理5,可得

‖ΔxaΔsc‖≤‖D-1Δxa‖‖DΔsc‖≤C(1+κ)5n3μ.

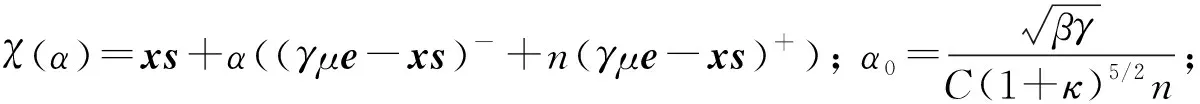
Δx(α)Δs(α)=α3(ΔxaΔsc+ΔsaΔxc)+α4ΔxcΔsc;μ(α)=x(α)Ts(α)/n.

引理6设(x,s)∈N(β,γ).如果α∈(0,α0],则‖Δx(α)Δs(α)‖1≤αnβγμ(α).

证明：由式(3),(4)可得x(α)s(α)=χ(α)+Δx(α)Δs(α).根据推论1,可得

其中第二个不等式用了Hölder不等式.注意到∑(γμe-xs)+≥0,于是

因此,由推论1可得

由式(8),(10),可得

其中h(α)=-βγ+αβγ+2α2C(1+κ)5n2+α3C(1+κ)7n3.对任意的α∈(0,α0],有

所以结论成立.由式(9),可得∑χ(α)≤nμ+α((γ-1)nμ+(n-1)βγμ)≤nμ+α(γ+βγ-1)nμ.

引理7设(x,s)∈N(β,γ),有μ(α)≤μ,α∈(0,α0].

证明：由式(10)中第一个等式及推论1知,对于α∈(0,α0],有

因为γ+βγ+1/5+1/100∈(0,1),所以对任意的α∈(0,α0],有μ(α)≤μ.

引理8设(x,s)∈N(β,γ).若μ(α)≤μ,则‖(γμ(α)e-χ(α))+‖1≤(1-nα)βγμ(α)e.

易知,χ(α)≥0.因此,

定理1设(x,s)∈N(β,γ),则由式(5)所定义的αc满足αc≥α0.

证明：由引理6和引理8知,对于α∈(0,α0],有

所以有x(α)s(α)≥(1-β)γμ(α)e>0.又因为x>0,s>0,由连续性可知α∈(0,α0],从而有x(α)>0,s(α)>0.证毕.

不失一般性,下面设σ=λ/2.

定理2设(x,s)∈N(β,γ),则有αf≥α0.

证明：由式(9),(10)及推论1,有

x(α)Ts(α)-(1-(1-σ)α)xTs≥αγnμ/2-2α3C(1+κ)5n3μ-α4C(1+κ)7n4μ∶=αnμf(α),

其中f(α)=γ/2-2α2C(1+κ)5n2-α3C(1+κ)7n3.对于α∈(0,α0],有f(α)≥f(α0)≥γ(1/2-2/C-1/C2)>0.结论成立.

定理3设(x,s)∈N(β,γ),则αg≥α0.

证明：令δ=γ+βγ+1/5+1/100.由引理7可证结论成立.

定理4算法1至多需要O((1+κ)5/2nlogε-1)次迭代终止.

3 数值结果

为检验算法的有效性,通过编写Matlab程序做如下数值实验.取γ=0.005,β=0.001,σ=0.000 1,ε≤1×10-7.

表1 例1的数值结果Table 1 Results of example 1

例2[10]取A=MTM+N-NT+D,其中:M=5-10rand(n);N=5rand(n);D是对角矩阵,且Di在(0,0.3)上平均分布,q的分量在(-500,500)上平均分布.利用算法1所得数值结果列于表2.

表2 例2的数值结果Table 2 Results of example 2

综上,本文分析了求解P*(κ)-LCP的二阶预估-校正内点算法,该算法具有目前不可行算法最好的多项式复杂度O((1+κ)5/2nL).数值实验验证了算法的有效性.

[1] Karmarkar N K.A New Polynomial-Time Algorithm for Linear Programming [J].Combinatorica,1984,4(4): 373-395.

[2] Potra F A,Stoer J.On a Class of Superlinearly Convergent Polynomial Time Interior Point Methods for Sufficient LCP [J].SIAM J Optim,2009,20(3): 1333-1363.

[3] Mehrotra S.On the Implementation of a Primal-Dual Interior Point Method [J].SIAM J Optim,1992,2(4): 575-601.

[6] Bai Y Q,Ghami M E,Roos C.A Comparative Study of Kernel Functions for Primal-Dual Interior-Point Algorithms in Linear Optimization [J].SIAM J Optim,2004,15(1): 101-128.

[9] LIU Hong-wei,LIU Xin-ze,LIU Chang-he.Mehrotra-Type Predictor-Corrector Algorithms for Sufficient Linear Complementarity Problem [J].Appl Numer Math,2012,62(12): 1685-1700.

[10] Kanzow C.Global Convergence Properties of Some Iterative Methods for Linear Complementarity Problems [J].SIAM J Optim,1996,6(2): 326-341.