船舶分段建造工程工期、成本、质量综合均衡优化研究

张 浩,张步华

(江苏科技大学 经济管理学院,江苏 镇江 212003)

工程项目管理中的工期、成本、质量管理是为了使工程项目实现所要求的质量、所规定的时限、所批准的费用预算而进行的全过程同步、全方位规划、组织控制与协调[1].船舶分段建造管理属于工程项目的范畴,因此,工程项目管理中的三大基本目标工期、成本、质量目标同时也是船舶分段建造工程的基本目标,这三个基本目标是一种相互依存、相互影响的对立统一关系,是工程项目目标成功实现的关键,只有同时考虑工期、成本、质量这三个要素才能有效的管理工程项目[2].由此可见,在工程项目管理过程中,为了实现工程项目的经济效益和社会效益,通常需要研究如何使工程项目要素优化组合、合理配置,保证工程项目资源的均衡性,从而在预算限度内实现工程项目的质量要求目标和工期目标[3].

国内学者对于船舶分段建造的工期、成本和质量目标的研究主要集中于对单个目标或两个目标之间的研究,如文献[4-5]是对工期进行的单目标研究;文献[6]则是从工期-成本优化进行的两目标研究;文献[7]则是从质量-成本进行的两目标研究；即使是在单目标或两目标的研究中,对成本方面的研究也大多是从财务核算的角度去进行研究的,如文献[8]是通过提出了双币成本控制标准管理模式和推行双币成本控制标准的策略来实现对造船企业的成本管理;而对质量的研究也更多的是从理论上研究如何控制生产质量,但与工程的质量目标相关的数学模型相对较少,如文献[9]是通过探讨造船模式转变对过程质量管理需求,研究适用于现代造船模式的质量控制技术.目前，很少有从工程项目管理的角度对船舶分段建造的工期、成本和质量目标进行综合优化研究.

船舶建造工程是一项复杂的系统工程,现代造船模式的本质是以“中间产品”导向的专业化生产,而船舶建造过程中最具有代表性的是中间产品生产区域，是对船体进行分段生产.因此,为了保障船舶建造工程项目的顺利进行,在船舶建造过程中,必须严格依照中间产品的要求,充分平衡项目的工期、成本和质量等要素,提高生产效率.

文中利用多目标优化理论对江苏省江阴市某船厂的一艘46 000 t散货船建立船舶分段建造的工期、成本质量综合优化模型,并在网络计划技术的基础上,使用粒子群算法对模型进行求解,从而得到最满意的方案和多个近似满意的备选方案,以作为船舶分段建造工程项目管理中的控制目标.

1 工期、成本、质量的相互制约关系

1.1 基本释义

1)工期

文中所述工期是指在船舶分段建造工程中的合理工期.文中对于船舶分段中工期的测定方法是由江阴市某船厂的工艺工程师和工人通过利用相似吨位的母型船的原始记录和统计资料,并参考新船的设计图纸、网络计划图、工艺规程、工人的技术水平和其它生产技术水平测算出来的各工序的标准工时、所允许的最短工时和最长工时.

2)成本

文中所述成本是指在船舶分段建造施工过程中所发生的各种费用总和，包括直接成本和间接成本,其中直接成本包括自制件、相关配套设施及原材料等费用；间接成本包括劳务费、管理费(如场地费)和专用费(如设计费、放样费)等费用.通常情况下,如果压缩工序工期,则必然需要相应的技术组织来做支撑,从而会增加一定的直接成本,因此,在限定的条件和范围内,压缩工序的工期会导致直接成本的增加;而间接成本通常是按照项目的工期来进行分摊的,因此,在特定的条件下,工期越短,间接成本就越低.文中对于船舶分段建造过程中所产生的各种直接成本的测算是通过江阴市某船厂过去建造的船舶的统计资料以及母型船的成本资料来制定估价标准表格,按标准填写重量、面积、长度、型号、规格,由船厂专业的估价人员进行估价.对于间接费用的测算则是采用分项计算方法,按有关文本(如《船舶产品价格计算标准》)并结合当前实际情况进行分项估算.

3)质量的量化

船舶建造过程中的质量管理是造船企业质量管理工作的重中之重.在实际的工程项目优化中,由于质量难以量化,因此人们通常只对工期或成本进行分析、优化,涉及到质量的数学模型通常较少.

文中为了研究船舶分段建造工程质量的量化问题,通过对船厂母型船的质量检验资料及参考文献[10]关于质量量化方法的研究,将通过采用0～1之间的数值来表示单项工作质量的可靠度,数值1表示质量可靠度最高,数值0表示质量可靠度最低.一个工程由多个工作组成,在确定整个工程项目总体质量可靠度时,必须考虑不同工作的重要性,如果因为某些工作质量的下降导致整个工程产生严重的质量问题,那么这些工作就需要分配更大的权重指标.文中做如下定义及假设:

定义1 单个工序的工作质量qi是此工作质量的可靠程度.

定义2 整个工程总的质量Q是通过对各单个工序质量进行加权得到.

假设1 单个工序的实际质量qi是实际持续时间ti的线性函数,且它们之间为正比例关系,即实际持续时间ti越小,实际质量qi越小.

通过假设1可得第i工序持续时间ti与质量qi(t-q)曲线的斜率为：

(1)

式中：βi为第i工序实际持续时间ti与实际质量qi(t-q)曲线的斜率；qni为第i工序的正常质量可靠度；qci为第i工序的最劣质量可靠度；tni为第i工序的正常持续时间；tci为第i工序的最短持续时间.

由此可得第i工序的实际质量为:

qi=qci+βi(ti-tci)

(2)

每个工序的质量qi应该介于正常质量和最劣质量之间,从而得到以下质量优化模型:

(3)

此模型表示工程总的质量可靠度是由各单个工序的质量可靠度按不同权重相加得到.式中：ωi为第i工序质量权重；qi为第i工序实际质量可靠度；Q为实际总质量可靠度；Q0为计划总质量可靠度.

1.2 质量和成本约束下的工期模型

一般情况下,如果工期缩短,则会导致成本发生变化,也可能会带来质量的下降,因此,质量、成本约束条件下的工期模型可以表述为:

目标函数:

minT

(4)

约束条件:

tci≤ti≤tni

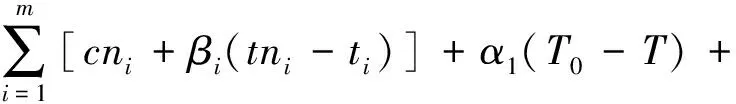
α2T≤C0

式中：T为实际总工期；T0为计划总工期；tci为第i工序最短持续时间；tni为第i工序正常持续时间；ti为第i工序实际持续时间；m为总工序数；C为实际总成本；C0为计划总成本；cni为第i工序的正常直接成本；βi为第i工序费用变化率；α1为计算工期大于或小于计划工期的奖罚系数；α2为单位时间内的间接费用.

1.3 质量和工期约束下的成本模型

船舶的订购价格一经确定,整个船舶的总成本及各个分段的成本也大致确定,在船舶的分段建造过程中只有降低建造成本,才能提高收益.但是,成本的降低不能脱离船舶的质量和工期的制约.因此,建立工期和质量约束条件下的船舶分段建造的成本优化模型.

目标函数:

minC

(5)

约束条件:

tci≤ti≤tni

T≤T0

1.4 工期和成本约束下的质量模型

对于任何船舶分段建造工程,分段的质量水平高低是和分段建造的工期和实际花费的成本相关的.为了寻求船舶分段在工期和成本约束条件下所应达到的满足项目要求的最佳质量水平,建立以下优化模型.

目标函数:

min(-Q)

(6)

约束条件:

tci≤ti≤tni

T≤T0

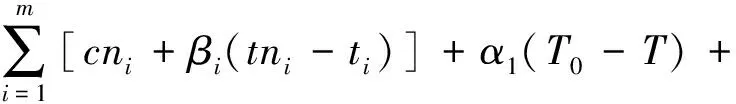
α2T≤C0

1.5 工期、成本、质量综合优化模型

当工程同时对工期、质量、成本都有要求时,那么就需要建立多目标综合优化模型.因此,建立的船舶分段建造综合均衡优化模型如下:

目标函数:

Z=min{T,C,-Q}

(7)

约束条件:

tci≤ti≤tni

T≤T0

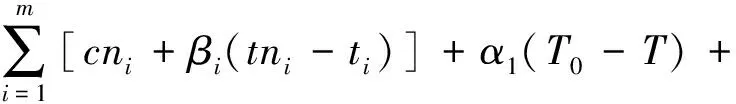
α2T≤C0

2 实例分析

2.1 工程概况

在船舶制造中,针对不同的几何形状,可以将船舶分段划分为平面分段和曲面分段.平面分段包括双层底分段、舷侧分段、甲板分段等货舱区域的分段,曲面分段包括舷部、舵部、机舱区域分段,通常来说,散货船等常规船舶的平面分段占据船体总分段数的60%以上,而对于一些大型或超大型的油轮,其平面分段所占的比例[11]更是达到80%.

此外,平面分段的结构相似性较高,加工工艺相似,通常可以采用流水线方式进行生产,文中选择以江阴某船厂的46 000 t散货船的平面分段中的一个分段作为实例来对模型进行验证.此船共有115个分段,货舱分段有96个,所以选取其中的货舱双层底中的一个分段(分段号109)来进行分析.表1为收集到的此分段统计数据表.由于该分段工期较短,因此可以认为影响工程质量的主要因素是工期和成本,而自然和社会因素对该分段的建造影响较小.船厂在建造船舶的过程中要求按照工期、成本、质量均衡的原则.该分段任务要求在70 d内完成,且要求质量可靠度不低于0.90.

表1 109分段工作相互关系以及参数估计Table 1 109 block mutual relations and working parameter estimation

2.2 参数估计

1) 质量权重的数据是由船厂质量管理专家及工艺工程师根据历史经验及本工序工作在整个分段工作中的重要性给定.

2) 假设单个工序在正常工期情况下完工的工作质量可靠度为1,单个工序最劣质量可靠度是由船厂质量管理专家根据船东对船舶的要求及母型船历史资料测算出来的最低质量可靠度极限值.

3) 根据工程实际情况及船厂相关奖罚制度设定:在赶工期情况下的奖罚系数为0.5万元/d;与实际工期有关的间接费用根据文中前述的测算方法得出为0.85万元/d.

4) 压缩工期所产生的费用变化率根据母型船历史资料统计分析得出.

2.3 计算工期、成本和质量

正常工期T0=80 d,最长工期T1=100 d,最短工期T2=59 d.

正常直接成本C1=68.25万元,最大直接成本C2=232.15万元.

正常质量可靠度Q1=1,最劣质量可靠度Q2=0.896 6.

2.4 建立模型

为了满足工程所要求的工期,并保证工程的成本和质量目标,工程管理者需要对工期进行合理的压缩,使工程实现工期-成本-质量目标的综合最优.根据表1建立其网络计划图(图1).

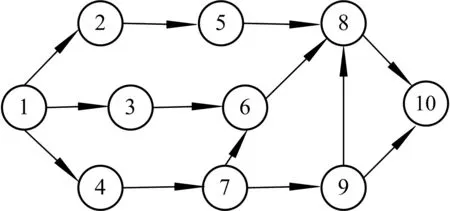
图1 109分段工程网络图Fig.1 Network planning of 109 block

本项目的综合优化模型为:

目标函数:

Z=min{T,C,-Q}

约束条件:

T≤T0

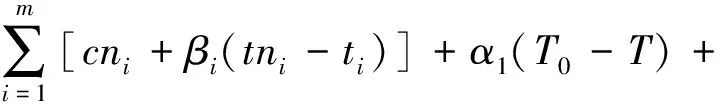
α2T≤C0

tci≤ti≤tni

求解这类模型的方法很多,如遗传算法、粒子群算法、模拟退火算法等.由于粒子群算法具有全局寻优及通用性的优势,文中采用粒子群算法对成本和质量的综合均衡优化模型进行求解.

2.5 粒子群算法的实现

在MATLAB的环境中,种群中的粒子代号及其速度都采用实数的编码格式.粒子的参数编码格式如图2.其中,dimsize表示参数的维度.粒子群编码[12]见图3,其中popSize表示粒子种群数.

X1,X2,X3,……,Xdim sizeV1,V2,V3,……,Vdim sizeF(X)粒子位置的各维表示粒子速度的各维表示适应度

图2粒子参数编码格式
Fig.2 Particle parameter encoding format

图3粒子群编码格式
Fig.3 PSO encoding format

对于粒子群算法参数的设定,因为工程共有10个工序,因此X为10维向量,且每个粒子的位置和速度都是10维的向量,学习因子设定为C1=C2=0.5,惯性权重从0.9减少到0.4,Vmax是搜索空间的宽度,算法的粒子群规模数是20,最大迭代次数为500次.应用MATLAB编程,运行100次,得最优解Z=[70,138.13,-0.931 1],即在满足工期等于70 d的情况下,工程的总成本为138.13万元,质量可靠度为0.931 1.

3 结论

文中将粒子群算法引入到船舶分段建造工程项目建造过程,并通过一个优化实例进行说明.通过实例的运算结果表明,经过工期优化及粒子群算法优化后,工期70 d,此时工程的总成本为138.13万元,质量可靠度为0.931 1,达到工程的预期要求.实例表明,粒子群算法可以准确且简单的解决船舶分段建造过程中的多目标优化问题,对船舶分段建造的多目标优化问题具有创新性的实际意义.

[1] Wysocki R K.有效的项目管理[M].北京:电子工业出版社,2009:4-50.

[2] 黄巍.项目管理中范围与时间、成本、质量的关系研究[D].上海:上海交通大学.2008,12:25-39.

[3] 李义华,王忠伟,庞燕.资源约束条件下工期、质量、成本综合均衡优化[J].中南林业科技大学学报:自然科学版,2008,28(6):101-105.

Li Yihua,Wang Zhongwei,Pang Yan.Proportional optimization of time,quality and cost under resource restriction[J].JournalofCentralSouthUniversityofForestry&Technology：NaturalScienceEdition,2008,28(6):101-105.(in Chinese)

[4] 曹大鹏,杨衡.基于JIT船舶分段建造调度问题研究[J].科学技术与工程,2010,07:4876-4881.

[5] 慕光宇,李莉,张文孝,等.基于CPM和挣值法的船舶建造项目进度控制的研究[J].科技管理研究,2011(7):206-208.

Mu Guangyu,Li Li,Zhang Wenxiao,et al.Research on the progress management in shipbuilding project based on CPM and earned value method[J].ScienceandTechnologyManagementResearch,2011(7):206-208.(in Chinese)

[6] 金朝光.船舶建造工程管理及供应链一体化研究[D].辽宁大连:大连理工大学,2002:37-57.

[7] 王社勤,李勇,罗乐,等.船舶企业质量成本分析管理[J].上海造船,2011(3):71-74.

[8] 孟凡生,尹鹏,周瑜,等.船舶企业成本控制模式研究[J].中国修船,2012,6(3):5-7.

[9] 汪稚棋,赵虹,王晓亮.现代造船模式下过程质量控制研究[J].造船技术,2011(4):1-4.

[10] 刘尔烈,张艳海.建筑施工项目进度、成本和质量目标的综合优化[J].天津理工学院学报,2001,17(2):90-93.

Liu Erlie,Zhang Yanhai.Comprehensive optimization of the time-cost quality control objectives of construction projects[J].JournalofTianjinInstituteofTechnology,2001,17(2):90-93.(in Chinese)

[11] 李宁.船舶制造平面分段流水线作业优化应用与研究[D].上海:上海交通大学,2007:1-3.

[12] 刘晓峰,陈通,张连营.基于微粒群算法的工程项目质量、费用和工期综合优化[J].土木工程学报,2006,39(10):122-125.

Liu Xiaofeng,Cheng Tong,Zhang Lianying.Applicaton of PSO to multiple objective project optimmization[J].ChinaCivilEngineeringJounal,2010,39(10):122-125.(in Chinese)