微型导弹蒙特卡洛打靶仿真研究

罗俏, 张伟, 李伟

(1.西北工业大学 航天学院, 陕西 西安 710072;2.西安长峰机电研究所, 陕西 西安 710065)

2012-10-15;

2012-12-26; < class="emphasis_bold">网络出版时间

时间:2013-04-09 09:58

罗俏(1986-)，男，湖南娄底人，硕士研究生，研究方向为飞行器动力学、制导与控制仿真。

微型导弹蒙特卡洛打靶仿真研究

罗俏1, 张伟2, 李伟1

(1.西北工业大学 航天学院, 陕西 西安 710072;2.西安长峰机电研究所, 陕西 西安 710065)

导弹在实际作战飞行中,由于环境因素和系统误差的影响,其姿态和弹道的参数与理想弹道的参数存在偏差。对一种微型导弹在飞行中受到的多种随机干扰因素进行分析,给出了各种干扰因素的处理方法,建立了导弹六自由度弹道蒙特卡洛打靶仿真模型。通过蒙特卡洛计算机打靶仿真,对导弹的命中精度进行研究,验证了仿真模型的准确性和仿真方法的有效性。

微型导弹; 六自由度仿真; 蒙特卡洛方法; 随机干扰

0 引言

近年来,战争的发展对武器打击的精确度提出了越来越高的要求,即对武器的命中精度要求越来越高,而精确打击武器首推导弹。随着现代武器的发展,导弹已经实现了从几公里到上万公里的全程精确打击,几十米到几公里的范围则基本由火炮武器来覆盖。但是,无论是传统的或是经过改进的火炮武器,其打击方式均是靠火力覆盖,不能实现精确打击。因此,为了实现对近距离小机动目标的精确打击,发展研制了一种精确制导的超近距微型导弹。本文旨在对微型导弹的命中精度进行仿真研究,以实现近距离精确打击。对导弹的命中精度进行研究,传统上依靠实弹打靶来实现,需耗费大量的人力、财力,同时在导弹预研阶段是不可能实现的;而采用计算机进行模拟打靶,能较快得到导弹的命中精度。因此,计算机仿真打靶成为研究导弹命中精度的一种重要手段[1]。采用蒙特卡洛法对超近距微型导弹进行模拟打靶,得到导弹的命中精度,为导弹的设计和性能验证提供方法和依据。

1 蒙特卡洛仿真方法

采用蒙特卡洛法进行导弹模拟打靶的基本步骤如下:

(1)根据导弹的运动特性以及典型的目标运动规律,建立导弹的六自由度弹道仿真模型;

(2)确定导弹飞行过程中受到的主要随机干扰因素及其分布规律;

(3)根据各种随机扰动因素的分布律,构造相应的数学概率模型;

(4)将随机扰动的抽样值加载到导弹六自由度弹道仿真模型,进行计算机模拟打靶,得到扰动弹道参数及弹着点参数;

(5)重复进行步骤(4),进行多次模拟打靶,获得多个随机弹道弹着点参数子样;

(6)对模拟打靶的结果进行处理,得到弹着点参数的统计特征值。

计算机模拟打靶流程如图1所示。

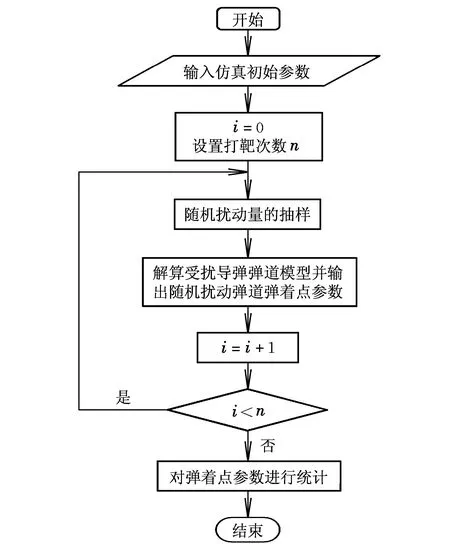
图1 计算机模拟打靶流程图Fig.1 Flow chart for computer simulated target practice

2 弹道模型及干扰因素处理

由文献[2]可知,导弹的运动方程组包括:导弹的质心动力学和运动学方程、弹体绕质心转动的动力学和运动学方程、质量变化方程以及坐标系转换角度几何关系方程等16个方程。导弹控制系统采用过载、弹体姿态角及角速率的反馈控制系统,其控制系统方程为:

(1)

将目标看作质点,目标的运动模型为:

(2)

导弹与目标的空间相对位置如图2所示。

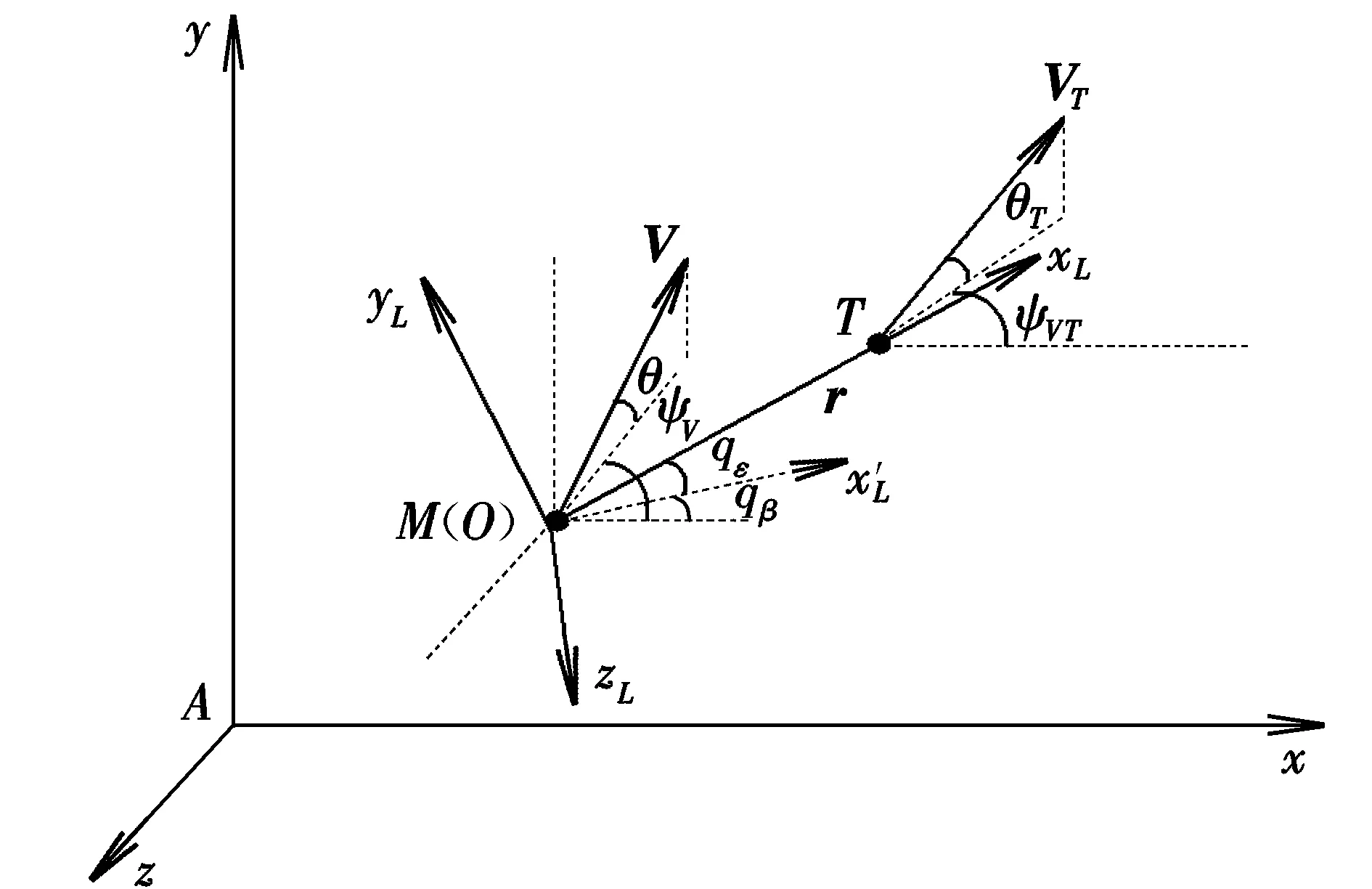
图2 导弹与目标的相对位置关系Fig.2 Relative position of missile and target

图中,OxLyLzL为视线坐标系,其原点O取在导弹的质心上;xL轴与导弹质心和目标质心连线平行,指向目标为正;yL轴位于包含xL轴的铅垂平面内,与xL轴垂直,指向上方为正;zL轴与其他两轴垂直构成右手坐标系。另定义:视线高低角qε为导弹目标连线矢量r与水平面Axz之间的夹角,若r在水平面之上,则qε为正,反之为负;视线方位角qβ为导弹目标连线矢量r在水平面Axz上的投影与Ax轴之间的夹角,沿Ay轴向下看,当Ax轴逆时针方向转到投影线上时,视线方位角qβ为正,反之为负。

由导弹与目标的空间相对位置,可推导得到导弹与目标相对运动关系方程为:

(3)

导弹制导律采用比例导引法,根据比例导引制导律定义,导引方程为:

(4)

导弹在飞行中,受到多种干扰因素作用,使得导弹的弹道参数偏离理想弹道而产生偏差。本文考虑的随机干扰因素主要有[3-4]:

(1)导弹结构参数误差,主要包括:推力大小偏差、质量偏差、转动惯量偏差;

(2)发射过程带来的干扰,不考虑导弹发射的动态过程,将发射过程造成的干扰综合成初始俯仰角偏差和初始偏航角偏差;

(3)阵风的影响,包括水平阵风Wx,Wz和垂直阵风Wy对导弹弹道的影响;

(4)弹上陀螺仪对弹体转动角速度的测量误差;

(5)控制系统向操纵系统反馈控制信号时由于系统白噪声产生的信号误差,这些反馈的控制信号包括俯仰角、偏航角和滚转角及滚转角速度的控制信号。

以上随机干扰因素均服从正态分布,在随机扰动模型中可以作如下处理[5]:(1)和(2)的干扰因素可以通过调整模型中各参数仿真初始值来实现,即在导弹弹道仿真模型中的原仿真初值m0,P0,Jx0,Jy0,Jz0,θ0,ψ0上分别加上m0r,P0r,Jx0r,Jy0r,Jz0r,θ0r,ψ0r得到蒙特卡洛打靶仿真的初始值。

阵风的干扰使得仿真模型中的气动力和气动力矩需要采用相对速度Vr、相对迎角αr和相对侧滑角βr进行计算。其中导弹的相对速度Vr=V-W。设导弹速度在地面坐标系中可以表示为V=[VxVyVz]T,风速在地面坐标系中可以表示为W=[WxWyWz]T,则Vr可由下式确定:

(5)

此时,只需将弹道仿真模型求解α,β和γV,方程中的θ和ψV替换为θr和ψVr,即可求出相对迎角αr、相对侧滑角βr和相对速度滚转角γVr。气动力和气动力矩的计算可以通过αr,βr和Vr进行求解,只需将原来求解气动力和气动力矩方程中的输入量V,α,β替换为Vr,αr,βr。此外,气动力是在速度坐标系中给出的,在将气动力投影到弹道坐标系时,需将速度滚转角γV用相对速度滚转角γVr来代替,同时还需要做适当的变换才适用于原来的动力学方程。假设在阵风干扰时的气动力为Fr=[XrYrZr]T,其中Xr,Yr,Zr分别为有阵风干扰时的气动阻力、升力和侧向力,经过变换Fr3=LT(β,α)L(βr,αr)Fr可将气动力投影到弹道坐标系中,此时的Fr3可适用于原来的动力学方程。

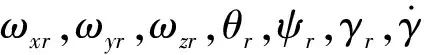
3 计算机模拟打靶及结果分析

基于建立的受扰导弹的六自由度弹道数学仿真模型,在VC++6.0环境下编写蒙特卡洛打靶仿真程序。其中,采用四阶龙格库塔方法来解算微分方程组,正态分布随机数根据中心极限定理得到。

首先将各项扰动因素设为零,打靶次数设为1,进行弹道仿真,将得到的导弹各项参数结果与理想弹道参数相比较,二者是一致的,可以验证仿真模型的正确性。再将打靶次数设为300,加载随机干扰进行蒙特卡洛打靶,得到导弹在Oxz靶平面内弹着点的分布情况如图3所示。图中,“*”为受扰导弹弹着点在靶平面的散布,“☆”为散布点的均值,即期望弹着点。

图3 导弹弹着点在Oxz靶平面内的分布情况Fig.3 Distribution of missile’s impact points on the Oxz target plane

对蒙特卡洛打靶结果进行统计分析,弹着点的数学期望值和方差计算公式为:

(6)

弹着点数学期望值和方差的参数统计值如表1所示。

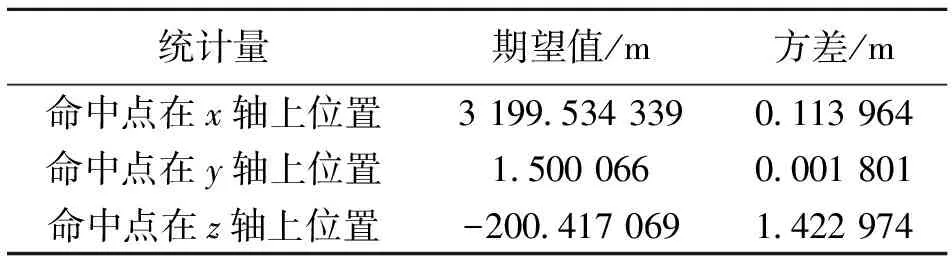
表1 导弹弹着点参数统计值Table 1 Parameters statistics of missile’s impact points

利用仿真得到的导弹弹着点散布的方差σx和σz,进一步可以获得导弹的圆概率误差(CEP),计算公式[5]为:

(7)

从计算机蒙特卡洛打靶仿真可得,采用蒙特卡洛法对导弹进行300次模拟打靶,所需机时不到2 h,所耗机时较少,能快速仿真得到导弹的命中精度;导弹的弹着点在Oxz靶平面内分布密集程度高,其散布服从正态分布规律,且平均弹着点位于靶平面的中心位置;由表1中导弹弹着点参数的统计量可知,导弹的期望弹着点与理想弹道弹着点(3199.506 081,1.499 910,-200.316 445)十分接近,且弹着点在三轴向的方差都较小,说明导弹在受到一定干扰因素作用时,在控制系统作用下,仍能达到较高的命中精度;由式(7)计算得到导弹的CEP=0.87 m,导弹的命中精度较高,相比打击相同距离目标的火炮,其精度要高出一个数量级,满足近距离精确打击的要求。

4 结束语

本文提出了考虑受到多种扰动因素作用时,导弹六自由度弹道仿真模型构建的方法,基于蒙特卡洛计算机模拟打靶,为导弹命中精度的验证和研究提供了仿真手段。基于VC++6.0平台开发的导弹蒙特卡洛打靶仿真程序具有很强的通用性和可移植性,通过改变仿真参数,可以应用于不同的导弹或火箭弹的打靶仿真,能快速仿真得到其命中精度。

通过蒙特卡洛打靶对微型导弹的命中精度进行仿真计算可知,导弹的命中精度较高,满足精确打击要求。仿真结果验证了导弹六自由度弹道仿真模型以及各扰动因素模型的准确性,同时也说明了采用蒙特卡洛方法对导弹进行计算机模拟打靶是有效、可行的。模拟打靶结果也可以为导弹研制、作战训练提供指导作用[6],具有一定的理论和实际意义。

[1] Hanson J M,Beard B B.Applying Monte Carlo simulation to launch vehicle design and requirements verification[J].Journal of Spacecraft and Rockets,2012,49(1):136-144.

[2] 李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2005.

[3] 孙艳馥,侯妮娜,郭红千.反坦克炮立靶密集度影响因素分析[J].四川兵工学报,2010,31(1):22-23.

[4] 金华,戴金海.某异型卷弧翼弹的蒙特卡洛计算机模拟打靶[J].航天控制,2007,25(2):52-56.

[5] 王华,徐军,张芸香.基于Matlab的弹道蒙特卡洛仿真研究[J].弹箭与制导学报,2005,25(1):181-183.

[6] 夏永春,刘足,张伟.基于仿真应用的火炮外弹道研究[C]//2011全国仿真技术学术会议论文集.银川,2011:105-109.

SimulationresearchofaminiaturemissilewithMonte-Carlomethod

LUO Qiao1, ZHANG Wei2, LI Wei1

(1.College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2.Xi’an Changfeng Research Institute of Mechanism and Electricity, Xi’an 710065, China)

In actual operational flight, due to the influence of environmental factors and system errors, missile’s attitude and trajectory parameters are deviated from the parameters of the ideal trajectory. The disturbances affecting the flight of missile are analyzed, and a disturbance handling method is presented. Then, a 6DOF of Monte-Carlo trajectory simulation model is established. From the simulation, the hit accuracy of the missile is studied, and the accuracy of simulation model and the validity of simulation method are verified.

miniature missile; 6DOF simulation; Monte-Carlo method; random disturbance

TJ765.4

A

1002-0853(2013)03-0265-04

(编辑：李怡)