基于规则形状模拟靶的弹着点快速计算方法

聂 凯,曾科军,栾瑞鹏

(中国人民解放军92124部队,辽宁 大连 116023)

在飞行器多发短间隔或多发齐射攻击目标的试验中,指挥员需要根据命中目标情况调整攻击诸元,快速准确地计算出弹着点位置对现场指挥决策意义十分重大。考虑安全因素,攻击过程中一般不派人员抵近测量,而是采用摄像测量系统采集实况影像的方式供指挥员决策。因此,如何基于实况影像和靶标形状快速计算出弹着点位置成为十分紧迫的问题。这里弹着点定义为飞行器命中目标的位置与靶心的相对位置关系,包含距离和方位两个要素。

传统的弹着点测量与计算多是用来测试射击密集度[1],其自动测量系统有双CCD交汇立靶[2-3]、光幕阵列天幕立靶[4-5]和声靶[6]等。这些测量和计算方法各有其应用场景和优缺点,本文讨论的弹着点计算不是针对射击密集度,而是针对大型飞行器现场准实时快速判定。摄像测量因布放简易,测量精度高,近来发展迅速[7-8]。通常摄像测量多采用多台光学设备如光电经纬仪、高速摄像机等交会测量,要求2台以上光学设备同步获取飞行器与目标遭遇图像,通过对图像进行特征提取和数据处理获得弹着点或脱靶量[9]。它采用包含多目标的图像称为同帧画幅[10],由于同帧画幅目标具有相同的测量设备角度误差、光学大气折射误差等系统误差,计算中可以抵消,因此可以获得高精度的同帧画幅目标相对位置。多台光学设备交会测量成本较高,布站条件要求复杂[3],因此也可采用单目测量的,但它需要小型雷达[11]等设备辅助,系统建造和使用也复杂。上述方法计算精度高,但很难达到实时或准实时要求,因此需要研究弹着点快速计算方法。

为了命中结果测量和计算的准确性,通常都会依地势构建规则形状如长方形、圆形等的模拟靶。这里以长方形模拟靶和靶心为十字架为例,采用实时回传图像,基于同帧画幅和标识物建立了弹着点计算模型,考虑有靶心和靶心炸毁两种情形,并给出了两种计算模型的误差快速修正方法,最后进行仿真分析和采用实际图像对计算方法进行验证。

1 规则形状模拟靶

在不需要毁伤效果测量的试验中,出于经济性等考虑,通常以规则形状模拟靶代替实体靶。在某飞行器多发短间隔攻击试验中,本文选取某山坡构建长方形模拟靶,依据地形布设单目高速摄像测量系统,并将图像实时回传至指挥中心。此时属于单目摄像测量进行定位,需要比双目测量更严格的限制和靶标保障条件。为此,对模拟靶进行了综合设计,采用长方形框架加十字架靶心,为了便于误差快速修正,长方形四条边采用红白相间隔3米的涂装。事前,需要对标识物点位、十字架纵、横边长度等进行精确测量。设飞行器在连续三帧图像上的位置为T0、T1、T,且T为靶面上的弹着点,飞行器、模拟靶和摄像机位置关系如图1所示。

2 基于靶心的弹着点快速计算方法

计算步骤:首先选取单目高速摄像测量系统回传图像中飞行器命中模拟靶时刻的特定影像,接着使用判读系统进行点位判读,将判读结果代入基于靶心的弹着点快速计算模型,经误差快速修正后得到弹着点位置。

对命中时刻图像的判读采用如图2所示坐标系形式,坐标原点O位于图像最左上角,X轴为水平方向,向右为正,Y轴为垂直方向,向下为正,T为弹着点。

2.1 基于靶心的弹着点计算模型

在计算前,已经对靶心、十字架、边框及其上标识物的位置和长度等参数进行精确测量。第一发攻击时,十字架还没有被炸毁,计算时选择十字架作为标识物。摄像机依山势布放,无法与十字架水平或垂直,所以十字架在图像中的位置不能在水平和垂直方向上,如图3所示。

计算过程为:

1)首先判读靶心O、A、B、C、D五点的像素数,通过计算A点和B点的像素差ΔX1和ΔY1,求出十字架横边的偏离角α,通过计算C点和D点的像素差ΔX2和ΔY2,求出十字架竖边的偏离角β;

2)接着判读弹着点T的像素数,计算它与靶心的像素差ΔX和ΔY;

3)假设弹着点像素数在水平、垂直方向上与AB、CD方向上的偏差为Δx和Δy,根据公式(1)计算出Δx和Δy;

(1)

4)假设十字架长和宽相等,且长度为m,弹着点T与靶心的距离在水平和垂直方向上的投影为ΔTx和ΔTy,根据公式(2),计算出ΔTx和ΔTy;

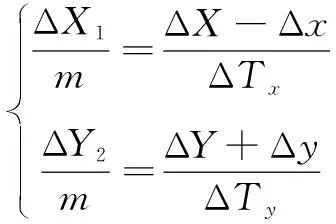
(2)

5)根据ΔTx和ΔTy的值,基于公式(3)计算出弹着点与靶心偏差的距离L和角度φ(以正北方向为0度,顺时针依次增大)。

(3)

2.2 基于靶心的误差快速修正方法

由于摄像机不是垂直正对靶面,根据摄像测量原理[7],物体在采集的影像中存在“近大远小”的误差,为了提高弹着点计算的精度,需要进行误差快速修正。

当靶心十字架还没有炸毁时,采用基于靶心十字架的误差修正方法,具体步骤为:

1)在试验前先采集一段影像,对图3上十字架的四个顶点A、B、C、D和离十字架较近竖边框的中点P、Q进行判读;

2)基于3.1节的公式(1)-(3)计算每个点位与靶心偏差的距离L和角度φ,并与实际进行对比,求出误差趋势和数值如表1所示;

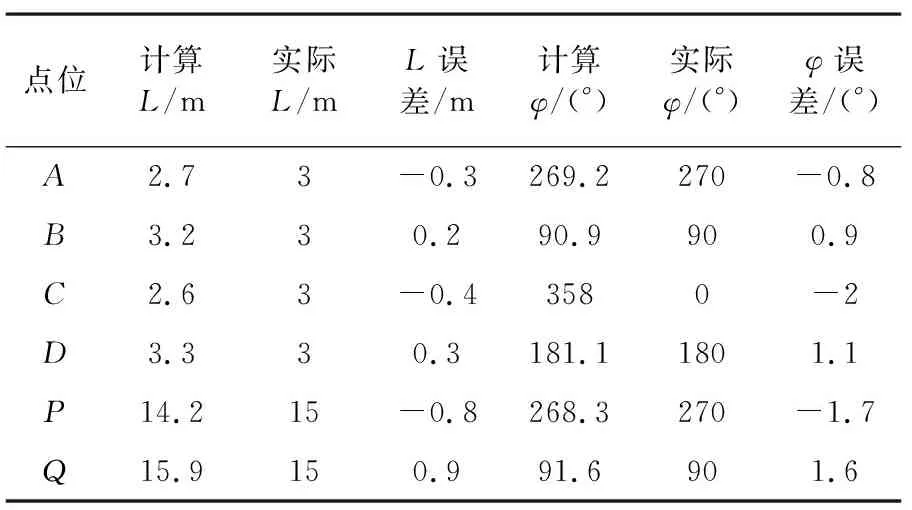
表1 基于靶心十字架的误差值

3)实际计算时,根据弹着点距离上述6个参考点的远近,基于表1对实际计算结果进行修正。如实际弹着点离B点较近,则对实际计算的L减去0.2 m,φ减去0.9°,实现误差快速修正。

3 基于边框的弹着点快速计算方法

根据历史经验,第一发飞行器通常会炸毁靶心十字架,后续的弹着点计算只能采用边框作为标识物。此时,需要调整第2节的弹着点计算模型和误差快速修正方法。

3.1 基于边框的弹着点计算模型

当十字架被破坏后,变成虚线,如图4所示,从图中可知,AB平行于两个横边框RS和WV,CD平行于两个竖边框RW和SV,以边框为标识物给出弹着点计算模型。

计算过程为:

1)首先判读R、S、W、V四点的像素数,假设弹着点离R点比较近,选择计算R点和S点的像素差ΔX1和ΔY1,求出横边框的偏离角α,通过计算S点和V点的像素差ΔX2和ΔY2,求出竖边框的偏离角β;

2)接着判读弹着点T的像素数,计算它与靶心的像素差ΔX和ΔY。因摄像机位置和角度没有发生变化,靶心像素数采用第2.1节判读结果;

3)假设弹着点像素数在水平、垂直方向上与RS、SV方向上的偏差为Δx和Δy,根据公式(1)计算出Δx和Δy;

4)当弹着点偏离靶心较远落在远处地面时,计算地面弹着点偏差Δx和Δy,还需考虑地面弹着点与靶面的高度差,采用公式(4)计算出图像上因地形起伏引起的弹着点像素位移δh,添加到Δx和Δy中[12]。其中,r为地面弹着点距离靶心的像素差,H为实况相机海拔高度,h为地面弹着点的海拔高度。

(4)

5)假设横边框长度为l,竖边框长度为n,弹着点T与靶心的距离在水平和垂直方向上的投影为ΔTx和ΔTy,根据公式(5),计算出ΔTx和ΔTy：

(5)

6)根据ΔTx和ΔTy的值,基于公式(3)计算出弹着点与靶心偏差的距离L和角度φ。

3.2 基于边框的误差快速修正方法

当靶心十字架被毁坏时,采用基于边框的误差快速修正方法,具体步骤为:

1)基于试验前采集的一段影像,对图4上边框的四个顶点R、S、W、V和离边框各6 m的点R1、S1、W1、V1进行判读;

2)基于2.1节的公式计算每个点位与靶心偏差的距离L和角度φ,并与实际进行对比,求出误差趋势和数值如表2所示;

3)实际计算时,根据弹着点距离上述8个参考点的远近,基于表2对实际计算结果进行修正。如实际弹着点离S点较近,则对实际计算的L加上2.2 m,φ加上5.6°,实现误差快速修正。

表2 基于边框的误差值

4 精度分析与验证

分析文献[8]和[13]可知,影响基于规则形状模拟靶的弹着点快速计算方法精度的主要因素有:目标像素判读误差、误差修正方法等。

4.1 目标判读精度分析

目标判读是摄像测量法的关键,其精度至关重要,计算中采用了对弹着点、十字架、边框等点位的判读结果。为研究不同目标判读结果对弹着点计算精度的影响,仿真中将目标判读精度设为0.5像素和1像素,弹着点距离偏差假设在5 m(基于十字架)、10 m(基于十字架)、15 m(基于边框)附近,摄像机标定误差等条件固定。目标判读精度对弹着点计算的影响见表3。

表3 目标判读精度对弹着点计算结果的影响

从表3可以看出,无论标识物是十字架还是边框,判读精度越高,弹着点计算精度也越高,因此计算过程中尽量采用清晰度高的图像。

4.2 误差快速修正方法分析

针对快速计算要求,在误差修正时,没有从摄像机分辨率、摄像机标定误差、布站几何等方面考虑,而是从工程实际出发,采用弹着点附近的标识物的先验误差值对实际计算结果进行修正。两种情况的误差快速修正方法,分别选择了6个标识点和8个标识点,总体来看,这些点位还是比较稀疏的,对于这种弹着点快速计算来说,能够满足精度需求。下一步,除了十字架和边框外,还计划在靶面内设置更多的标识点,形成满足粒度需求的误差修正网格,这样就能够为计算提供更详细准确的先验信息,弹着点计算的精度更高。

4.3 实际图像验证

试验中,使用本方法进行了多次弹着点快速计算,所有飞行结束后都会去靶区进行实际弹着点位置测量,把这些测量结果作为弹着点真值。本文选取两次试验的图像对本方法的精度进行验证,飞行器攻靶示意图像如图5和图6(靶心被毁坏)所示,两次弹着点计算结果精度如表4所示。

表4 两次弹着点计算结果精度

表4可以看出,无论基于靶心的还是基于边框的弹着点快速计算方法,距离偏差经误差修正后计算误差小于1 m,角度偏差经误差修正后计算误差小于5°,满足弹着点快速计算和现场指挥决策的精度需求。且从计算结果看,越靠近靶心,距离与角度偏差的计算误差越小,这与实际情况相符。从历次试验结果看,整个计算过程在5分钟之内完成,满足准实时要求。

5 结束语

针对提供结果快速的实际需求,利用单目摄像测量和飞行器命中目标时刻影像,提出了一种基于规则形状模拟靶的弹着点快速计算方法。本文以长方形加十字靶心为例,针对有靶心和靶心炸毁两种情形建立了弹着点计算模型,并给出了两种计算模型的误差快速修正方法。通过仿真分析和实际图像验证表明,这种方法相对简单,采用同帧画幅抵消了一定量的系统误差,采用弹着点附近的标识物的先验误差值对实际计算结果进行修正,提高了定位速度和精度。下一步将在靶区设置更多的标识点,形成满足粒度需求的误差修正网格,为计算提供更详细准确的先验信息,进一步提高计算精度。