混合遗传算法在最优Lambert轨道转移设计中的应用

黄勇, 李小将, 张东来, 周乃东

(1.装备学院 研究生院, 北京 101416;2.空军航空大学 飞行训练基地, 吉林 长春 130022)

2012-09-18;

2012-12-18; < class="emphasis_bold">网络出版时间

时间:2013-04-09 09:58

黄勇(1986-)，男，江苏大丰人，博士研究生，研究方向为武器系统运用与仿真。

混合遗传算法在最优Lambert轨道转移设计中的应用

黄勇1, 李小将1, 张东来1, 周乃东2

(1.装备学院 研究生院, 北京 101416;2.空军航空大学 飞行训练基地, 吉林 长春 130022)

研究了初始位置、目标位置和转移时间均不固定的双冲量Lambert转移问题,旨在实现燃料和转移时间的综合最优。在对Lambert飞行时间定理推导的基础上,提出了一种遗传算法和迭代法相结合的优化算法,并给出了算法的设计步骤;同时,对影响遗传算法寻优性能的两个参数进行了自适应调整,提高了算法的收敛性。最后,通过两个实例验证了所提算法的有效性和准确性。

轨道转移; 最优化; 混合遗传算法

0 引言

航天器最优冲量轨道转移是航天领域备受关注的一个问题,最常用的方式有Hohmann转移和Lambert转移。其中,Hohmann转移仅适用于共面或异面圆轨道转移,而Lambert转移既可用于共面轨道转移,也可用于异面椭圆轨道转移,因此,Lambert转移问题一直以来都是该领域的研究热点。

给定航天器的初始位置矢量、目标位置矢量和转移时间就可确定航天器的运行轨道,此即典型的Lambert转移,围绕这一问题已形成了多种求解方法。文献[1-2]介绍了求解航天器Lambert轨道转移常用的一些方法,主要采用迭代思想,包括Battin方法、Gauss方法和普适变量法。文献[3-4]分别给出了多圈Lambert转移的算法,解决了因航天器变轨时间较长所产生的燃料骤增问题。实际上,还可以通过优化转移的始末位置以及转移时间来获得燃料和时间的综合最优解。近年来,发展迅速的智能优化算法为获得此类问题的全局最优解提供了有效途径。文献[5]采用遗传算法计算了最优双脉冲Lambert转移,但仅限于始末轨道均为圆轨道且初始位置固定的转移。文献[6]研究了遗传算法用于求解任意形状轨道、初始位置有约束的燃料和时间综合最优转移问题,但也只考虑了共面、目标位置固定的转移。文献[7-8]分别采用自适应模拟退火算法和自适应模拟退火遗传算法解决了初始位置、目标位置和转移时间均不固定的Lambert最优转移问题。在工程实际中,通常给定初始时刻追踪航天器和目标航天器的轨道要素,并限定在一定的时间范围内实现两航天器的交会。针对此类问题,文献[9]引入调相时间,将调相时间和转移时间作为优化变量,利用引导型人工免疫算法研究了总时间约束条件下燃料最省的Lambert转移。

本文研究了初始位置、目标位置和转移时间均不固定的双冲量Lambert转移问题。

1 Lambert双冲量轨道转移数学模型

对于单圈轨道转移情况,Lambert飞行时间定理可以表述为[10]:

μ1/2Δt=a3/2[(α-sinα)-(β-sinβ)]

(1)

μ1/2Δt=a3/2[2π-(α-sinα)-(β-sinβ)]

(2)

μ1/2Δt=a3/2[(α-sinα)+(β-sinβ)]

(3)

μ1/2Δt=a3/2[2π-(α-sinα)+(β-sinβ)]

(4)

式中,μ为地球引力常数;Δt为转移时间;a为转移轨道半长轴;α和β为Lagrange参数,其几何意义见文献[11],可由下式求得:

α=arccos(1-s/a)

(5)

(6)

s=(r1+r2+c)/2

(7)

式中,c为初始点到目标点的距离;r1,r2分别为初始点和目标点的地心距。

转移轨道的半通径p同样可以用α,β表示为:

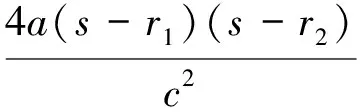
(8)

(9)

根据以上公式,可以确定转移轨道中a和p的计算公式,如表1所示。其中,Δθ为转移轨道上初始点位置矢量和目标点位置矢量之间的夹角;Δtm为对应转移轨道为最小能量椭圆时的转移时间,其具体定义参见文献[11]。

表1 a和p计算公式的选择Table 1 Selection of calculation formula of a and p

若直接利用迭代方法求解上述Lambert方程是很困难的,为便于求解,作如下变换。令:

(10)

则式(1)～式(4)可整理为:

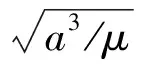
(Δθ≤π)

(11)

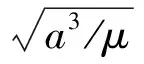
(Δθ>π)

(12)

以λ为迭代变量,对于给定的交会时间tf,有f(λ)=tf-Δt,利用牛顿迭代法可以求出λ。

图1描绘了双脉冲Lambert轨道转移问题。根据初始轨道的轨道根数H1={a1,e1,i1,Ω1,ω1,θ1}和目标轨道的轨道根数H2={a2,e2,i2,Ω2,ω2,θ2},可以求得航天器在初始点和目标点的位置矢量(r1,r2)和速度矢量(V1,V2),再选定转移时间Δt,可根据Lambert方程计算出转移轨道的轨道根数Hf,从而计算出转移轨道上初始点速度Vf1和目标点速度Vf2。因此航天器两次轨道转移所需要的总速度脉冲增量为:

ΔV=|Vf1-V1|+|V2-Vf2|

(13)

图1 双脉冲Lambert轨道转移Fig.1 Two-impulse Lambert orbital transfer

2 优化问题的描述

2.1 设计参数选取

选取初始轨道的真近点角θ1、目标轨道的真近点角θ2和Lambert轨道转移时间Δt作为优化问题的求解参数,即选择参数X={θ1,θ2,Δt},该轨道转移的优化问题就转化为参数X的优化问题。

2.2 目标函数的选取

航天器轨道转移过程中消耗的能量与时间是此消彼长的关系,节省能量和减少轨道转移时间是相互抵触的,须对二者进行折衷,是典型的多目标优化问题。这里将性能指标定为脉冲增量与转移时间的线性加权和:

J(X)=k1ΔV+k2Δt

(14)

式中,k1,k2分别为脉冲增量和转移时间的加权系数,其取值范围为[0,1],且有k1+k2=1。

2.3 约束条件

在轨道转移过程中,总要满足一定的约束条件,如参数的取值范围及工程实际的一些限制。本文主要考虑以下几点:

(1)轨道转移时间Δt的取值范围为[tLmin,tLmax],这里tLmin取为0;tLmax取相同轨道半径的圆轨道霍曼转移时间的0.4～1.0倍。

(2)初始轨道θ1、目标轨道θ2的取值范围可在(0,2π)内根据需要自行设定,从而保证航天器可以在初始轨道任意位置变轨以及在目标轨道任意位置入轨。

(3)轨道转移消耗的总能量一般存在上限约束,即ΔV≤Vmax,本文将航天器的最大脉冲消耗限制为10 km/s。

(4)工程上,Lambert轨道转移的半长轴和偏心率也有上限约束,一般而言,a≤107km,e≤0.7。

3 混合遗传算法设计

3.1 混合遗传算法设计步骤

遗传算法作为一种概率搜索算法,它的寻优结果具有一定的随机性,且随着优化参数的增多极易陷入局部最优解[12]。

为减少遗传算法的寻优参数,提高其寻优效率,本文设计了一种将遗传算法与迭代法相结合的混合遗传算法,该算法的思想是:主程序采用遗传算法初始化产生代表Δt和θ1的种群,并对其寻优,子程序运用迭代通过式(11)和式(12)计算个体适应度值。设计主程序步骤如下:

(1)采用二进制级联编码,按Δt精确到1 s,θ1精确到0.1°,分别确定各自的二进制码长,产生初始种群(Δt,θ1)。

(2)将种群中个体解码后输入到个体适应度值计算子程序进行适应度值的计算,并根据子程序得到的适应度值进行排序,保存当代适应度最高的个体。

(3)依据种群中各个体的适应度值,采用比例选择算子选择与父代规模相同的新的种群。

(4)在种群的遗传操作过程中,采用自适应交叉和变异算子,若达到设定的遗传代数,则解码输出最优个体,结束程序,否则转至步骤(2)继续进化。

个体适应度计算子程序接收到主程序产生的(Δt,θ1)后,计算出θ2,进而计算出Δθ,p1,p2及其他相关参数。根据Δθ选择p和迭代法中间变量λ的计算公式来计算Δt的最小值,并以此判断主程序任意产生的Δt是否有意义;在确保Δt有意义后,计算出a和p,进而计算出个体的适应度值,否则最小化个体的适应度值。

3.2 遗传算法的自适应调整

遗传算法运行过程中,交叉概率Pc和变异概率Pm是影响遗传算法的关键所在,直接影响算法的收敛性。Pc,Pm选取过大会使遗传算法成为随机搜索,选取过小又不易跳出局部极值点。针对此问题,文献[13]提出了自适应遗传算法,即Pc和Pm的选取能够随适应度函数自适应调整,在保证种群多样性的同时,提高遗传算法的收敛性。经过改进,遗传算法参数自适应调整表达式为:

(15)

(16)

式中,Pc1取为0.8;Pc2取为0.5;fmax为种群中的最大适应度值;favg为每代群体的平均适应度值;f′为交叉的两个个体中较大的适应度值;Pm1取为0.1;Pm2取为0.05;f为要变异的适应度值。

4 算例仿真及分析

算例1:仿真初始轨道和目标轨道参数如表2所示,二者均为圆轨道,k1=1,k2=0,求燃料最优解。这里需对初始轨道的真近点角θ1加以确定,否则对于任意的θ1,目标轨道上都存在对应的θ2,使得轨道转移所需能量最优。

表2 算例1初始轨道和目标轨道参数Table 2 Initial and target orbital elements of case 1

对于轨道半径之比小于15.58的两共面圆轨道间的转移,双脉冲Hohmann转移为最省燃料转移,将其结果与本文优化算法求得的最优解进行对比,结果如表3所示。结果表明,两种方法求得的最优解偏差很小,说明了本文优化算法的可行性和准确性。

表3 算例1优化结果比较Table 3 Comparison of optimization results of case 1

图2给出了群体适应度值随遗传代数变化的过程。由图可见,群体的最小适应度值在遗传初期变化较大,随着遗传代数的增加逐渐收敛;群体的适应度均值也随着遗传代数的增加,逐渐向最小适应度值逼近。这表明群体中适应度值较大的个体依次被淘汰,较优个体依次被保留,群体中的个体差异不断减小并逐渐趋于最优值。

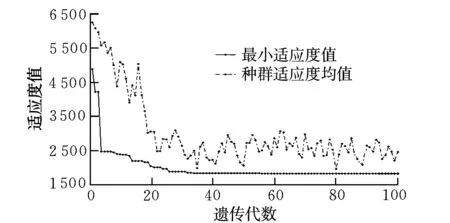
图2 适应度变化曲线Fig.2 Curve of fitness variation

算例2:仿真初始轨道和目标轨道参数如表4所示,二者位于异面椭圆轨道上。

表4 算例2初始轨道和目标轨道参数Table 4 Initial and target orbital elements of case 2

分别选取两组不同的k1,k2对算例2中的Lambert转移进行优化,表5为优化结果。其中,第1组为燃料最优解,第2组为燃料和时间综合最优解。从优化结果可以看出,随着k1减小、k2增大,时间在最优性能指标中所占比重增大,而脉冲增量所占比重减小。故最优解中脉冲增量增大、转移时间减小,且转移轨道的偏心率增大,这是符合常理的。

表5 算例2优化结果Table 5 Optimization results of case 2

需要指出的是,Lambert转移燃料和时间综合最优问题的各项优化参数,其值是介于转移燃料最优和时间最优二者之间的。而时间最优对应的转移轨道为抛物线,长半轴趋于无穷大,这对于纯粹的双脉冲Lambert转移是没有意义的,故本文未将其列出。

5 结束语

本文通过对Lambert飞行时间定理的推导,建立了适合于遗传算法和迭代法求解的Lambert双冲量转移模型,简化了问题的求解过程。所提混合遗传算法有利于双脉冲Lambert转移的快速优化设计,引入的参数自适应调整增强了算法的收敛性。通过两种不同情况下的仿真算例验证了算法的有效性和准确性,可为其他类型的优化问题提供一定的方法借鉴。

[1] Battin R H.An introduction to the mathematics and methods of astrodynamics[M].Reston,VA:AIAA,1999.

[2] Curtis H D.Orbital mechanics for engineering students [M].Elsevier,2010.

[3] Shen Haijun,Tsiotras P.Optimal two-impulse rendezvous using multiple-revolution Lambert solutions[J].Journal of Guidance,Control,and Dynamics,2003,26(1):50-61.

[4] Arlulkar P V,Naik S D.Solution based on dynamical approach for multiple-revolution Lambert problem [J].Journal of Guidance,Control,and Dynamics,2011,34(3):920-923.

[5] Spencer D B,Kim Y H.Optimal spacecraft rendezvous using genetic algorithms [J].Journal of Spacecraft and Rockets,2002,39(6):859-865.

[6] 陈统,徐世杰.基于遗传算法的最优Lambert双脉冲转移[J].北京航空航天大学学报,2007,33(3):273-277.

[7] 李小将,赵辉,赵伟.基于自适应模拟退火算法的最优Lambert双冲量转移[J].装备指挥技术学院学报,2011,22(4):50-54.

[8] 卢山,陈统,徐世杰.基于自适应模拟退火遗传算法的最优Lambert转移[J].北京航空航天大学学报,2007,33(10):1191-1195.

[9] 彭坤,徐世杰,陈统.引导型人工免疫算法的最优Lambert变轨[J].北京航空航天大学学报,2010,36(1):6-9.

[10] 李栋林,黄福铭.基于Lambert问题的精确拦截与交会策略研究[J].飞行力学,2008,26(2):57-59.

[11] 郗晓宁,王威,高玉东.近地航天器轨道基础[M].长沙:国防科学技术大学出版社,2003.

[12] 王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002.

[13] Srinivas M,Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithm [J].IEEE Transaction on Systems,Man and Cybernetics,1994, 24(4):656-666.

ApplicationofhybridgeneticalgorithminoptimalLambertorbitaltransferdesign

HUANG Yong1, LI Xiao-jiang1, ZHANG Dong-lai1, ZHOU Nai-dong2

(1.School of Graduate, Academy of Equipment, Beijing 101416, China;2.Base of Flight Training, Aviation University of Air Force, Changchun 130022, China)

The two-impulse Lambert transfer problem with unfixed initial position, final position and transfer time was studied in order to optimize combination of the fuel and transfer time. Based on the derivation of the Lambert flight time theorem, an optimization algorithm combining genetic algorithm and iteration method was presented as well as its design process. Meanwhile, two parameters affecting genetic algorithm performance were adjusted adaptively, which can improve the algorithm’s astringency. Lastly, the validity and accuracy of the hybrid genetic algorithm were validated by two examples.

orbital transfer; optimization; hybrid genetic algorithm

V448.2

A

1002-0853(2013)03-0269-04

(编辑：李怡)