基于非奇异终端滑模的复合控制导弹反演设计
2013-11-04舒燕军唐硕
舒燕军, 唐硕
(西北工业大学 航天学院, 陕西 西安 710072)
2012-10-09;
2012-12-25; < class="emphasis_bold">网络出版时间
时间:2013-04-09 09:58
国家高技术研究发展计划(863计划)基金资助(2011AA7022014)
舒燕军(1985-),男,江苏沭阳人,博士研究生,研究方向为飞行器制导与控制、建模与仿真。
基于非奇异终端滑模的复合控制导弹反演设计
舒燕军, 唐硕
(西北工业大学 航天学院, 陕西 西安 710072)
针对轨控式复合控制导弹制导末端的姿态控制问题,结合反演控制、二阶非奇异终端滑模和非线性干扰观测器技术,设计了一种新的反演滑模姿态控制方法。在反演设计的第一步采用动态面法,避免了传统反演设计存在的“计算膨胀”问题,并使姿态角跟踪误差收敛至原点附近任意小的邻域内;第二步设计引入了二阶非奇异终端滑模,使得角速率跟踪误差在有限时间内收敛至零,同时消除控制量的抖振现象。采用非线性干扰观测器补偿系统不确定性,并基于Lyapunov稳定性理论证明了闭环系统所有误差信号最终有界。仿真结果表明了所设计的轨控式复合控制导弹制导末端姿态控制方案的正确性与有效性。
反演设计; 非奇异终端滑模; 动态面; 干扰观测器; 复合控制导弹
0 引言
新一代防空导弹普遍采用直接力/气动力复合控制方式。根据直接力/气动力复合作用机理的不同,复合控制导弹分为姿控式和轨控式。前者的直接力系统作用在姿控回路,与气动力系统配合共同建立弹体姿态;后者的直接力系统作用在制导回路,提供直接过载,能够快速修正弹道偏差。轨控式复合控制导弹的直接力系统一般在与目标遭遇1 s左右开启[1],在提高导弹可用过载的同时,也给气动力姿态控制系统带来强烈的耦合干扰。此外直接力系统开启后会产生推力偏心和复杂的侧向喷流干扰效应[2]。以上三点因素会使弹体姿态在短时间受到强烈的扰动,因此轨控式复合控制导弹制导末端的控制是具有较大不确定性的非线性系统,目前主要的研究方法有基于小扰动线性化方法[3]、动态逆和神经网络结合方法[4]以及自抗扰控制方法[5],寻求更有效的非线性系统设计方法来提高导弹自动驾驶仪性能成为研究的难点。
针对传统反演控制中的“计算膨胀”问题[6],文献[7]提出了动态面法,即引入一阶积分滤波器估计虚拟控制律的导数,避免对虚拟控制律的重复求导,从而降低控制器的复杂性。针对终端滑模控制量中存在的奇异问题,文献[8]提出了非奇异终端滑模。将反演控制与滑模控制相结合成为目前的研究热点,文献[9]将反演思想与二阶线性滑模控制方法结合,消除了抖振现象,但由于线性滑模的渐近收敛特性,子系统对上一步虚拟控制量的跟踪误差不能在有限时间内收敛到零,增加了累积误差。文献[10]在反演设计的最后一步采用终端滑模控制器,使跟踪误差在有限时间内收敛,但未考虑奇异值问题。
本文针对轨控式复合控制导弹的不确定严格反馈块控非线性模型,提出了一种基于非奇异终端滑模的动态面反演姿态控制方法。
1 复合控制导弹的数学模型
本文的轨控式复合控制导弹模型描述见文献[11]。进一步可将上述模型写成严格反馈块控非线性系统的一般形式:
(1)
式中,X1=[α,β,γ]T;X2=[ωz,ωy,ωx]T;舵偏u=[δz,δy,δx]T为系统的控制输入;ψ1和ψ2为内部不确定性和外界干扰构成的复合干扰;系统输出为y=X1。忽略舵偏对气动力的影响,即令h1(X1)=0,则复合控制导弹的模型满足严格反馈块控形式。控制系统的设计目标是消除复合干扰对系统的影响,使得γ=0,且α和β能精确稳定跟踪给定的指令信号。
2 非线性干扰观测器(NDO)技术
NDO对于系统中的不确定性具有良好的估计能力,可以补偿不确定性对系统的影响,提高整个闭环系统的控制效果[12]。考虑如下含有不确定性和干扰的非线性系统:

(2)
式中,ψ=Δf(x)+Δg(x)u+d为复合干扰,d为外界扰动;x,ψ,d∈Rn,u∈Rm;f(x),Δf(x):Rn→Rn;g(x),Δg(x):Rn→Rn×m;f(x),g(x)中的各个函数充分光滑,且满足局部Lipschitz条件。
针对上述系统构造如下的非线性干扰观测器逼近复合干扰ψ:

(3)

定义NDO的观测误差为:
(4)
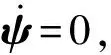
=L(x)[θ+p(x)+f(x)+g(x)u]-
L(x)[f(x)+g(x)u+ψ]
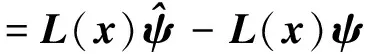
=-L(x)ed
(6)
构造如下的Lyapunov函数:
(7)
将上式两边对时间t求导得:
(8)

3 反演滑模控制器设计与稳定性分析
为便于控制律设计,首先给出如下假设和引理。
假设1:g2(X1,X2)非奇异且范数有界;
假设2:g1(X1)可逆且范数有界,即存在正常数g1l和g1h,使得g1l≤‖g1(X1)‖≤g1h。
引理1:设K:D→R为定义域为D⊂Rn且包含原点的连续正定函数,并设对于某个r>0有Br⊂D,则对于所有x∈Br,存在定义在[0,r]上的κ类函数a1和a2,满足a1(‖x‖)≤K(x)≤a2(‖x‖)。如果D=Rn且K(x)是径向无界的,则存在κ∞类函数a1和a2在[0,∞)上有定义,使得上式对于任意x∈Rn都成立。
步骤1:用动态面方法设计虚拟控制量X2d。
考虑闭环系统(1)的第1个子系统:
(12)
定义跟踪误差向量:
z1=X1-X1d=[z11,z12,z13]T
(13)
z2=X2-X2d=[z21,z22,z23]T
(14)
式中,X1d为给定的姿态角指令信号。对式(13)求导并结合式(12)得:
(15)
根据上式设计如下虚拟控制律:
(16)

(17)
由NDO原理可知,存在L1正定,且满足
(18)
为了避免下一步设计中对虚拟控制律υ1求导,从而引起“计算膨胀”问题,本文根据动态面法的要求,使用一阶低通滤波器对虚拟控制律υ1进行滤波,滤波动态方程如下:
(19)
式中,τ1>0为滤波器时间常数;滤波器输出X2d为υ1的估计值。
定义滤波误差为:
m1=X2d-υ1
(20)
对上式求导得:
(21)
将式(14)、式(16)、式(17)和式(20)代入式(15)得:
(22)
针对闭环系统式(12)构造如下的Lyapunov函数:
(23)
对V1按时间t求导并将式 (18)、式(21)和式(22)代入得:
(24)
若闭环系统的第2个子系统可以实现精确跟踪,即z2=0,则有:
(25)
由引理1知存在κ∞类函数η1和η2,使得:

(26)
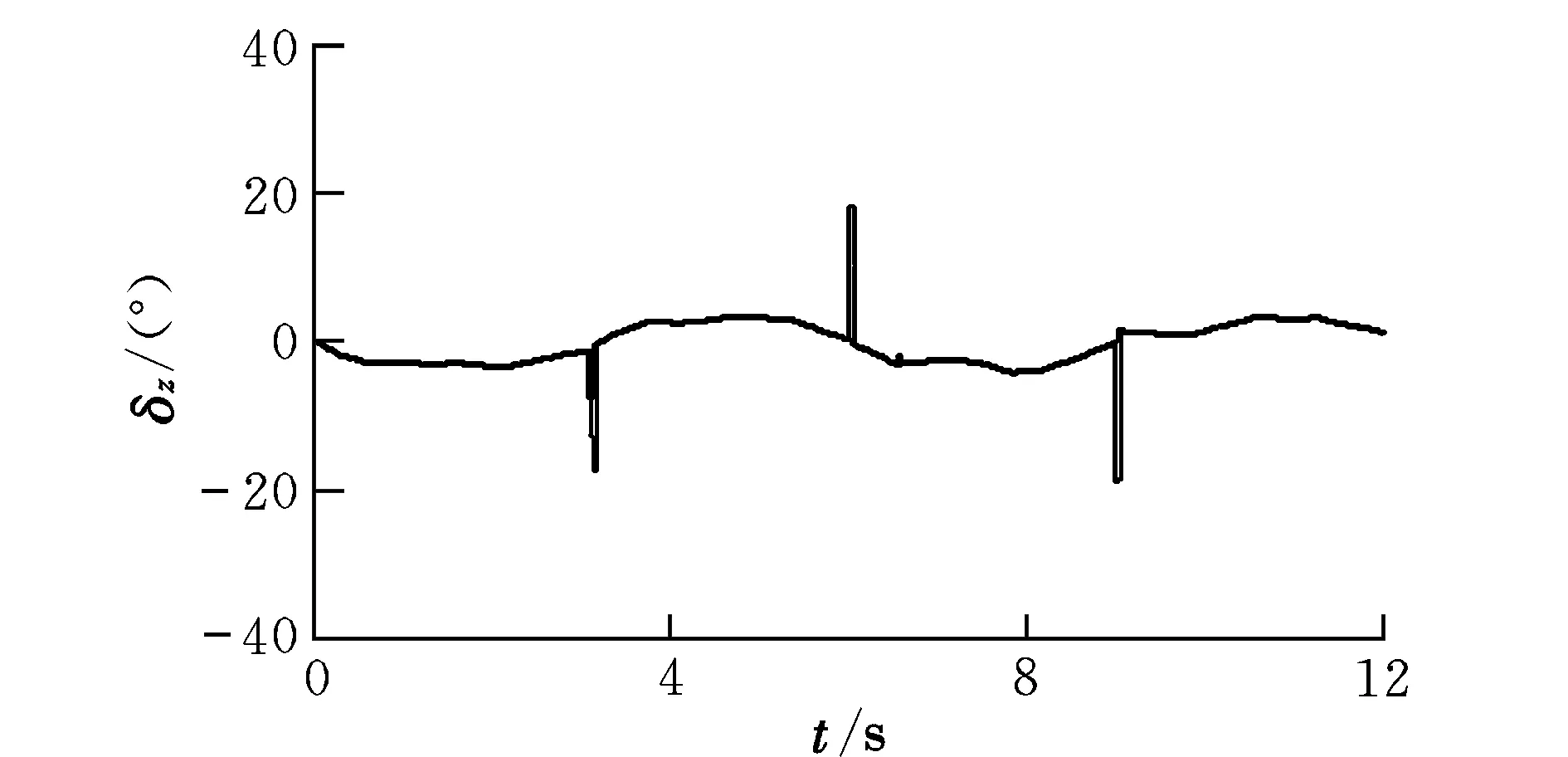
由Young不等式ab ≤-‖m1‖2/τ1+‖m1‖2/2+η2/2 (27) (28) (29) 将式(26)~式(29)代入式(25)得: (‖L1‖-1)‖e1d‖2+η2/2 (30) (31) 由式(23)易知‖z1‖≤2c0,‖m1‖≤2c0,‖e1d‖≤2c0。因此,当跟踪误差z2=0时,在虚拟控制律X2d作用下,闭环系统(2)的第1个子系统所有信号均有界,且跟踪误差z1及观测器误差e1d指数收敛至原点的一个任意小的邻域: Ω0= {z1,e1d|‖z1‖≤2c0, ‖e1d‖≤2c0,‖m1‖≤2c0} 步骤2:基于非奇异终端滑模设计控制律u,使角速率跟踪误差z2在有限时间内收敛到零。 考虑闭环系统的第2个子系统: (32) 如果采用传统的线性滑模,则只能保证误差渐近趋近原点,本文采用二阶非奇异终端滑模,可实现跟踪误差z2在有限时间内收敛至原点,并且可以避免普通终端滑模在原点附近可能发生的奇异问题。 定义如下二阶非奇异终端滑模超平面: (33) (34) 通过适当选取参数ρ1,ρ2和β可调节z2的收敛速度。 由假设1知g2可逆,因此本文采用如下控制律: (35) (36) 则由前面的NDO原理可知,存在L2正定,满足 (37) 对式(33)求导并将式(2)和式(35)代入得: (38) 定义闭环系统(2)第2个子系统的Lyapunov函数: (39) 对V2按时间t求导并将式(37)和式(38)代入得: ‖L2‖‖e2d‖2 ‖L2‖‖e2d‖2 ≤0 (41) 由Lyapunov稳定性理论可知,在控制律u作用下闭环系统的第2个子系统可实现对虚拟控制量X2d的精确跟踪,当跟踪误差z2=0后,在X2d作用下,闭环系统可实现对姿态角指令信号X1d的精确跟踪。 在系统存在复合干扰的情况下,为了验证本文设计的控制方案性能,下面将上述控制律用于某型复合控制导弹的姿态跟踪控制。 为了模拟直接力系统对自动驾驶仪的耦合干扰作用,在俯仰、偏航和滚转通道各加入300 sinπtNm的干扰力矩,并设气动参数向下摄动30%。仿真参数设置如下:导弹初始姿态角:α0=0°,β0=0°,γ0=0°;指令姿态角:αc=5°,βc=5°,γc=0°。控制器各设计参数取为:ρ1=5,ρ2=3,β=diag[1,1,1],k1=k2=[3,5,8];低通滤波器的时间常数τ1=τ2=0.01;NDO设计参数取为j11=j12=j13=3,l11=l12=l13=3。舵偏须满足限幅为±30°的物理特性要求。 图1~图3分别为有、无NDO干扰补偿情况下迎角、侧滑角和滚转角的跟踪曲线。可见由于NDO对系统不确定性的补偿作用,反演滑模控制律可实现对指令姿态角的快速精确跟踪。 图1 迎角跟踪曲线Fig.1 AOA tracking curve 图2 侧滑角跟踪曲线Fig.2 Slideslip angle tracking curve 图3 滚转角跟踪曲线Fig.3 Roll angle tracking curve 图4~图6分别为三个通道的控制舵偏曲线。可见采用二阶非奇异终端滑模设计的控制量比较平滑,有效消除了传统滑模控制存在的抖振现象,且舵偏均满足限幅要求。 图4 俯仰舵偏角曲线Fig.4 Curve of pitch rudder angle 图5 偏航舵偏角曲线Fig.5 Curve of yaw rudder angle 图6 滚转舵偏角曲线Fig.6 Curve of roll rudder angle 由仿真结果可知,本文设计的基于非奇异终端滑模的动态面反演姿态控制方案具备良好的动态性能和跟踪精度,在有外部干扰和气动参数摄动的情况下具有很好的鲁棒性,且控制量平滑无抖振,满足舵机物理特性要求。 本文针对带有不确定性的复合控制导弹严格反馈块控非线性模型,设计了一种基于非奇异终端滑模的动态面反演姿态控制器。反演设计的第一步采用动态面法设计虚拟控制律,消除传统反演设计中的“计算膨胀”问题,使姿态角跟踪误差收敛至原点附近任意小的领域内;第二步设计采用非奇异终端滑模使系统的角速率跟踪误差在有限时间内收敛至零,并利用非线性干扰观测器在线逼近系统的复合干扰,使得系统对于外部干扰和气动参数摄动具有良好的鲁棒性。 [1] 李玉林,杨树兴.先进防空导弹直接力/气动力复合控制关键技术分析[J].兵工学报,2007,28(12):1523-1527. [2] 王宇航,马克茂.直接力与气动力复合控制系统姿态稳定问题研究[J].宇航学报,2007,28(4):840-844. [3] Rui H,Koichi S.Autopilot design for a missile with reaction-jet using coefficient diagram method[R].AIAA-2001-4162,2001. [4] Choi Y S,Lee H C.Autopilot design for agile missile with aerodynamic fin and side thruster[C]//SICE Annual Conference.Fukui,2003:1476-1481. [5] 王宇航,姚郁,毕永涛.基于自抗扰的直接力与气动力复合控制系统设计[J].宇航学报,2009,30(4):1544-1550. [6] Stansky A,Hedrick J K,Yip P P.The use of sliding modes to simplify the backstepping control method[C]//Proceedings of the American Control Conference.Albuquerque,New Mexico,1997. [7] Swaroop D,Gerdes J C,Hedrick J K.Dynamic surface control of nonlinear systems[C]//Proceedings of the American Control Conference.Albuquerque,New Mexico,1997. [8] Man Zihong,Paplinski A P,Wu H R.A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators [J].IEEE Transactions on Automatic Control,1994,39(12):2464-2470. [9] 顾文锦,赵红超.反舰导弹基于反演的二阶滑模控制[J].弹箭与制导学报,2003,23(4):97-100. [10] 周丽,姜长生,都延丽.一种基于反步法的鲁棒自适应 终端滑模控制[J].控制理论与应用,2009,26(6):678-682. [11] 王宇航.基于ADRC的直接侧向力-气动力复合控制 系统设计[D]. 哈尔滨:哈尔滨工业大学,2009. [12] Chen Wenhua,Donald J B,Peter J G,et al.A nonlinear disturbance observer for robotic manipulators [J].IEEE Transactions on Industrial Electronics,2000,47(4):932-938. Backsteppingcontrolforblendedcontrolmissilebasedonnonsingularterminalslidingmode SHU Yan-jun, TANG Shuo (College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China) Based on backstepping design,second-order nonsingular terminal sliding mode control and nonlinear disturbance observer,a new backstepping sliding mode controller is proposed for the blended control missiles dynamics. In the first step of the backstepping design,the dynamic surface control strategy was employed to eliminate the “explosion of terms” by introducing a first-order filter to obtain the differentiation of virtual control inputs,and attitude tracking error is proved to converge to an arbitrary small neighborhood of the origin. Second-order nonsingular terminal sliding mode control was then utilized to drive the angular velocity tracking error to converge to the origin in a finite period of time. Nonlinear disturbance observers were adopted to compensate for the uncertainties in the system. Using the Lyapunov stability theorem,it is proved that all signals in the closed loop system are ultimately bounded. Finally, simulation results demonstrate the superiority and effectiveness of the control scheme. backstepping design;nonsingular terminal sliding mode;dynamic surface;nonlinear disturbance observer;blended control missiles TJ765 A 1002-0853(2013)03-0260-05 (编辑:崔立峰)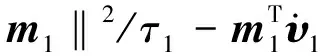






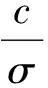






4 仿真分析





5 结束语
