论一种缘自认知心理学及教育学研究的数学认知过程

王名扬，徐沥泉，徐利治

（1.无锡市教育研究中心，江苏 无锡 214001；2.大连理工大学 数学科学学院，辽宁 大连 116024）

20世纪60年代后心理学从行为主义研究阶段发展到认知革命时期，并开始关注数学教育革新问题.无可非议，认知心理学的知识建构主义等学说，对促进数学教育研究深层次问题，已产生重要影响[1～3].

在方法论上，认知心理学从近现代计算机科学的发展中得到了重要启示，一是主要采用了信息加工的观点形成知识建构理论，二是认为一般正常人的大脑（简称“人脑”）基本上是按照计算机的模型来工作的.其实计算机模型原本都是由人脑结合实际需要按照合理的客观逻辑规律设计出来的.因此计算机也都是人脑工作的产物.

说到事物的本质，还必须返回到“科学的反映论”观点[4].按照反映论，人脑是具有以概念形式反映客观现象规律的能力的机制，这种机制及其功能都是有机生命体经历长期进化的结果.详言之，人脑本身是一种客观演化过程的产物，很自然具有客观地反映事物及其关系的本能，而且高层次的本能中还包含有“抽象概括能力”以及遵循客观逻辑法则创建关系结构（模式）的能力，甚至还具有预见事物关系的能力，即想象与猜想的能力.

正因为人脑本能中显示出层出不穷的主观能动性，以致曾有些心理学家与数学家们，都不自觉地特别强调科学创造性思维的人的内部心理过程的主观性特征，而忽视了事物的客观性本源.事实上，无论是知识的获取过程与创建过程，都是主体（人脑）与客体（事物现象关系及规律等）的反映与被反映的相互作用过程.从这一点来看，皮亚杰（J.Piaget）在发生认识论原理中提到的“同化”与“顺应”两个概念，还是十分正确的[5].

现在要来谈数学的一种认知过程，即“数学的现象、心象、抽象、操作”过程，或简称“三象一作”过程.根据反映论观点，能比较清晰地阐明这种认识过程及其在数学教育上的意义.

1 数学是探究数学现象的科学

这里不是要讨论数学的对象及其意义的问题，只是想说明数学教学是阐述并运用“数学现象规律”的科学.国内外许多数学家都是赞同“数学现象”这一说法的.例如中国已故的杰出数学家华罗庚就曾在科普讲演中，提到数学是研究数学现象的观点.德国著名数学家希尔伯特（D.Hilbert）的青年时代的同学兼好友胡塞尔（Hursserl）曾从学习数学科学开始，创始了哲学上的“现象学研究”.

很显然，现实世界中或人为设计构造中，凡出现的种种数量关系、空间形式以及一定条件下的随机性现象等，都属于数学现象.所以算术、代数、几何、概率论与统计数学等，都是论述“数学现象”的学科.从哲学上看，凡事物都有“量”的侧面，并能引出量的规定性，因此如果着眼于量的侧面考察种种事物及其间的关系时，所能见到的种种量性现象都可称之为“数学现象”.这样看来，近现代发展起来的数学诸分支，例如分形理论、小波分析、金融数学、非线性分析等等，都可以说成是探究数学现象的学科了.

值得注意的是，自然界、人世间存在着大量数学现象，而且数学现象也可以人为地创设出来.例如，各种棋类游戏都是人类设计出来的，但一经设计出来后，各种棋谱所蕴涵的量性关系，便成为客观的数学现象了，人们就只能遵循逻辑法则对其进行客观地分析研究.

2 从现象和心象到抽象

人们从儿童、少年、青年到成年，在生活实践与学习过程中，会不断地接触种种数学现象，这就会通过耳目等器官的感知在头脑中形成种种带有直观性的图像，即心智图像，简称“心象”（mental picture）.这在现代认知心理学与教育心理学里已有许多论述.

简单说来，数学心象就是数学现象在人们心目中呈现的一类未经理性分析的直觉形象.例如，少年儿童看到纸上画的一个圆周后，就会在头脑中留有该圆周的心象，当眼见许多具体的圆形事物后，脑海中就会有一种带有共性的圆的印象，这就初步走向抽象阶段了.

正因为人脑是具有抽象本能的，因此当青少年学习平面几何时，很自然就会自动完成圆的概念，即几何上圆的概念——那是一种绝对完美的由一个几何点围绕一个中心形成的理想化轨迹.古代哲学家柏拉图（Plato）甚至把这种抽象化的圆视之为超越经验的属于“理念世界”的东西.

经历许多万年的进化和遗传，固然人类的大脑都具有抽象概括的本能，但人在成长过程中，却是需要通过生活实践和学习训练才能不断唤醒和增长这种抽象能力的.事实上，由于人们的生活实践经历以及学习与工作生涯是各不相同的，所以人们之间的属于高层次的抽象能力还是颇有差别的.但是，最基本的抽象本能，确实是人人具备的.否则，人们就不可能适应通常的社会生活了.

一般说来，如果没有耳闻目睹或接触过具体的数学现象，就不可能产生直观性的数学心象，而不通过心象的积累、变化、组合及相互联结与综合等过程，也就不可能形成概括性的抽象概念.人们想获得高度总结性的科学知识，总是要经历这样的认知过程.但认知过程中还包含一个重要的“操作阶段”，那就是对知识的不断运用和不断再认识再提升的阶段.所以“三象一作”过程才是一种较完整的认知过程.

3 “三象一作”认知过程的进一步说明

以上只是按照科学反映论观点简要地解释了“三象一作”过程的含义.现代人使用计算机工具还可以有目的地去汇集和发现数学现象，为完成认知过程做准备.例如，研究“实验数论”的学者，就是有意识地利用计算机实验手段去罗致数学现象的.第二阶段就是依靠头脑的想象和默思去形成数学心象.这种心象就是数学现象在人脑中形成的映像，其间存在着“对应关系”，但这种映像往往是变动不定的，有时还是十分模糊的.第三阶段就是通过诸多心象的变动、累积、归纳和综合，使得具有提取“共性”本能的人脑形成数学概念.这样就达到了认知的“抽象阶段”.到了这一阶段，人脑还能很自然地按照事物关系的“对应原理”创制出表征数学概念实体的数学符号以及符号逻辑语法的数学名词及专用语言.最后，第四阶段就是在合乎逻辑法则的条件上操作运用抽象的数学知识与数学方法（包括数学符号及语言的运用）去处理数学问题并进一步去发展数学理论知识.

4 “三象一作”认知过程在数学教育上的意义

在数学教育上主要有如下3点意义.

（1）强调数学知识的本源是具有客观性的“数学现象”，这样就有利于使那些接受现代数学教育的青年学子，不容易受到种种唯心论思想的诱惑.

（2）对于数学的学习者而言，如能懂得或遵循“三象一作”认知过程，就能理解数学科学中的抽象知识与普遍方法的来源，实际是以数学现象为基础的.这就能启发学习者懂得创造知识的途径，就是要重视数学现象的汇集、整理和分析，从而就能乐于去处理生活中以及应用学科中出现的众多数学题材并研究实际应用问题.

（3）从教学过程来看，教师的重要职责，就是要有意识地设计一种学习情景，能促使学习者有兴趣地去发掘数学现象，主动观察数学现象，并能从中形成可以作为抽象背景的种种数学心象，最后还要鼓励学习者能从抽象过渡到操作阶段.

当然，从心象、抽象到数学操作，这其间有许多事情要做，按照知识“建构主义者”的观点，整个过程是要依靠学习者本身的自觉主动性来进行的.杰出的教师应是良好的指导者和顾问，也是讨论问题的主要设计者和参与者.

5 几个典型例子

很明显，中学数学教材中的许多题材内容，都是和广泛而丰富的“数学现象”相关联的，但是这里并不赞成把生活中的烦琐实例作为数学应用例子，写进教材中去.因为这会损伤学习者的兴趣，并不利于学习者按“三象一作”的认知过程学好数学知识与数学技艺.只有那些富于启发性的，或能引发好奇心的，或具有历史兴趣的数学现象题材，才有助于培育青少年的数学智能，从而才能考虑选入教材中去.

为了让初中学生也能理解“三象一作”的认知过程，不妨选择3个最简单而熟知的例子.一个是从商高的“勾股定理”说起，另外就是对欧拉（L.Euler）解答七桥问题的重新回顾和关于质数（“素数”——prime numbers）无穷多的论证过程.

（1）中国《周髀算经》上提到“商高答周公问”的故事，说到“勾三股四弦五”的数学现象（图1）.直角三角形之高称为“勾”，底边称为“股”，斜边为“弦”.

后人可能会问：已知勾为3、股为4，为什么弦长一定是5？为了从理性上肯定这一现象，当然是需要证明的.研究者相信，商高一定是从观察中看到了这一现象的，很可能他已察知下述特殊事实（图2）.

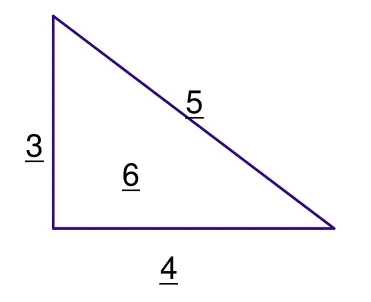
图1 勾股定理图示（一）

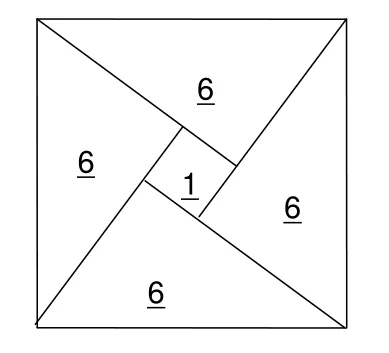
图2 勾股定理图示（二）

假设勾为3 m、股为4 m，则直角三角形之面积为6 m2.将这样4个三角形可拼合成如图2的正方形，易见中央的小正方形的面积为(4-3)2=12=1 m2.于是可知大正方形为4×6+1=25 m2，其边长（弦）当然是=5 m了.

纸上画出的如上图形，实际上已成为心目中的“几何现象”.而在几何图形中，线段有长度而无粗细，所以面积的计算是绝对精确的，这里已包含初步的数学抽象.事实上，古代欧几里得创著“几何原本”时已完成了这些数学上的初步抽象，事实上可将4个同样的直角三角形拼合成大正方形，从而可证明一般形式的“勾股定理”，又称毕达哥拉斯（Pythagoras）定理，这一技巧已被中国三国时期的学者赵爽所创用[6].

数学抽象的重要方式之一就是由特殊形式推广到一般（普遍）形式，很自然，按照赵爽的作法，可将4个同样的一般形式的直角三角形拼合成图3.

假设直角三角形的勾、股、弦长度分别为a，b，c，不妨说b>a.从图3易见小正方形面积为(b-a)2，而4个三角形的面积之和为2ab.因此总的面积为c2=(b-a)2+2ab=a2+b2.

这就是一般形式的勾股定理.它表示为3个线段长度数量间的关系，数学史上又称它为“数的勾股定理”，它比“形的勾股定理”（即以勾与股为边的两个正方形等于弦为边的大正方形面积的命题）在意义上更为宽广.

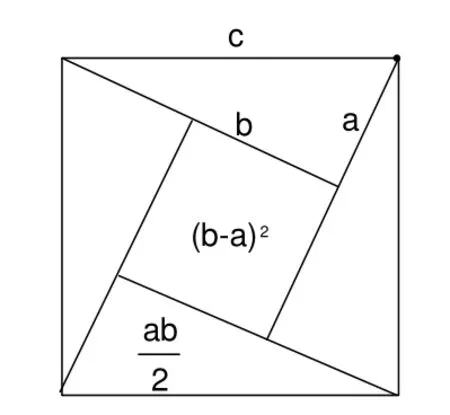
图3 勾股定理图示（三）

在数量乘法操作上，有mc2=ma2+mb2(m>0)，于是“形的勾股定理”就不必再局限于正方形面积间的关系了.例如可以有图4和图5的变形：

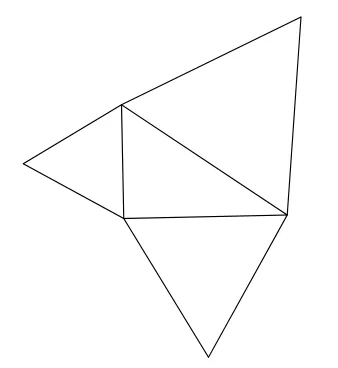
图4 勾股定理变形（一）

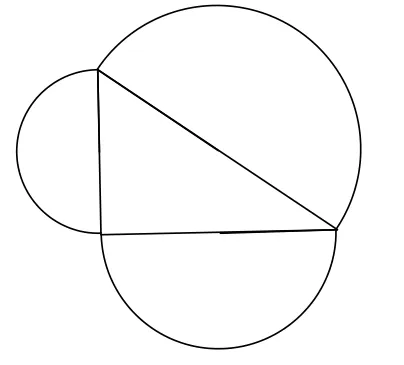
图5 勾股定理变形（二）

在这些图形面积关系中，正方形已换成正三角形与半圆，当然它们间仍保持有“两个小图形面积之和等于大图形面积”的数量关系.

上述例子说明，从特别的具体例子所显示的数学现象出发，经过观察发现关系，再经过抽象（推广）获得普遍定理，从而由操作还可得出一些异于原先命题陈述形式的新推论.

（2）在数学文献或刊物上常被引用的另一例子是18世纪出现在欧洲普鲁士哥尼斯堡（Koenigsberg）的一个故事，那就是关于“七桥问题”的故事.已有些科普文章讨论了这一数学历史故事在数学文化教育上的意义.但在这里研究者却要将它作为“三象一作”认识过程的一个例子来讨论.

据史料记载，1735年旅居俄罗斯圣彼得堡（St.Petersberg）的数学家欧拉（L.Euler）曾接到哥尼斯堡大学的学生写给他的一封信，要求解答“一次走过7座桥的事情”总是办不到的原因.

7座桥如图6所示.

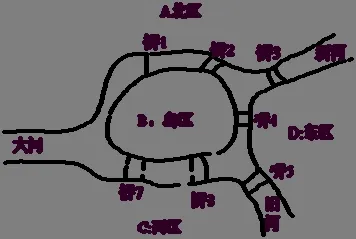
图6 哥尼斯堡七桥示意

这是涉及线路拓朴的图论问题，所以是一个属于数学现象方面的问题.当年哥尼斯堡大学的学生们虽未能解决这一问题，却知道求教于数学家，这说明他们还是高明的[7].

果然，欧拉通过抽象和操作，解决了这一问题，将“不可能性”的数学证明回信作答，使大学生们非常满意.

面对上述数学现象问题，可以想到欧拉采取的一个重要步骤，就是设法将该问题，基于“对应原则”，抽象成为一个“数学模型”问题.

不愧为杰出的数学家，欧拉立即将“桥”抽象成为“线”，将通过的地点“岛”及“半岛”及“两岸”抽象成为“点”，于是一次走过7桥的问题便对应地成为一笔画，如图7的问题.

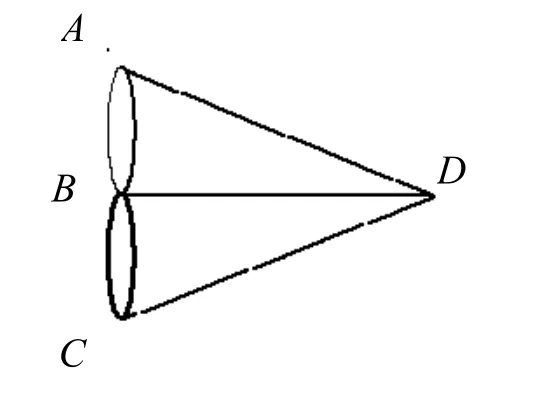
图7 哥尼斯堡七桥问题抽象转化示意图

只须证明上述图形不能一笔画出来，就能解决“七桥问题”，接下来的数学操作就是分析一笔画的特征.凡一笔画中通过的联结点，一进一走，总是通过偶数条线，故可简称之为“偶点”，只有画中的起点和终点可能是“奇点”，即通过奇数条线的点，而当起点终点重合时，就变成了封闭图形，那就不存在奇点了.

所以一笔画的特征（必要与充分条件）就是至多只可能有两个奇点.可是图7中的4个点都是奇点，并不符合一笔画的充要条件，因此答案只能是“不可能”.

显然上述解题过程，也是符合“三象一作”的过程的.在这个过程中，抽象与操作（包括推理分析）显然是最主要的步骤.

（3）中学生都知道质数（primes）有：2，3，5，7，11，13，17，23，29，31，……古代欧几里得（Euclid）曾在《几何原本》中证明了一条定理，说“质数有无穷多”.

相信每一个中学生，都会连续不断地写出一系列质数来，通过计算实践，会直观地猜想到“质数应有无穷多”.

质数从小到大会继续地出现的这种现象，就成为人们心目中的心象，心象导致猜想.于是人类心智的理性要求本能，就会促使人们去寻求“猜想事实必然成立”的证明方法.这就进入了“抽象”和“操作”阶段.欧几里得的认识过程完成了这两个阶段，才证明了“质数无穷多”定理.

首先，欧几里得认识到“无穷”是个抽象概念，质数无穷多的抽象表述为：在由小到大排列的任意n个质数2=P1，P2，P3，…，Pn，之后，一定总是存在更大的质数P>Pn.（因为n为任意，这就表明了质数确有无穷多的意思）

最后一步是“操作”：即通过逻辑推理去证明P（>Pn）的存在性，欧几里得构造了下列自然数：P1P2P3…Pn+1=m.

这里的m是个有限正整数，用P1，P2，P3，…，Pn去除m时都得余数1，因此，要么m本身是质数，当然它就大于Pn；要么m不是质数，它就会有质数因子P＞Pn.不论如何，这就证明了必有大于Pn的质数存在.因此定理获证.

关于“质数有无穷多”的客观现象，欧几里得使用数学推理方法证明了它，也就是从理性上彻底认识了这种现象的客观真实性，而表述这一客观现象的数学定理，就是“三象一作”的认知过程的产物.学生们通过这样的认知过程，也就完成了知识在头脑中的构建.

无论是在初等数学或是高等数学中，都有许多很有趣味的属于现实性的数学现象方面的疑难问题，是通过抽象和操作（包括分析、推理及论证）两大步骤获得解决的.抽象的重要作用就是提取数学现象中的关键本质，使之成为简化了的纯粹的数学模型问题，然后再通过分析推理或计算（甚至包括计算机的使用）去解决问题.

6 把“三象一作”用于中小学数学教学

由于许多数学教材，编入较多形式化的题材，并注重形式化操作性的训练，以致使不少青少年惧怕数学或厌烦数学.这其间的一个关键问题，就是忽视了数学现象与现象中出现的疑奇问题.遗忘了数学的本源——数学现象，学习者只是和抽象的形式化符号打交道，或只是背诵凝固化的数学语言，自然就会感到索然无味了.希望“三象一作”的认知方法引入数学教学后能有助于改变这些现象.

事实上数学现象是数学形式化题材的生命之源，也是数学生动直观心象的客观背景，学习者在使用数学符号作形式化推演之前，如果在头脑中已有了一系列直观心象，就会感到推理演绎是很自然的，是有兴味的，而并非是空洞无物的无意义的符号游戏.

儿童和青少年来到芸芸众生的世界后，对大千世界里的种种带有奇妙结构的客观现象，都会有情不自禁的好奇性.数学现象里就有许多美好的事物，所以在数学教学中，有意识地启示、鼓励，或促使学习者面对数学现象、观察数学现象，让数学现象成为心目中生动的心象.再让学习者学会数学中常用的抽象方法，则学习者肯定就会爱好数学，如此继续努力下去甚至可能成为善于使用数学或创造数学知识的人才.

当然，就大众化数学教育的目标而言，提倡“三象一作”的认知数学，决不是要求学习者都能成为数学专才，这是不必要的，也是不可能的.而合理的要求是希望学习者按“三象一作”的认知方法，学完中学数学后，至少能理解数学是研究客观现象规律的科学，这些现象及其规律是在大自然界、人世间处处存在且需要理性地对待和处理的.所以体现数学教育的功能之一，就是要让学习者能获得“理性精神”的熏陶.再者，通过一定层次上的教学“三象一作”的认识过程，使学习者至少能体会到科学的认知方法和知识的创新方法.这也是数学教育应产生的另一功能[8].

[1]谢明初，朱新明.认知心理学视角下的数学教育[J].数学教育学报，2007，16（1）：12-16.

[2]张洪魏.关于学生数学认知理解的思考[J].数学教育学报，2006，15（4）：14-16.

[3]涂荣豹.数学教学认识论[M].南京：南京师范大学出版社，2003.

[4]徐利治，王前.数学与思维[M].长沙：湖南教育出版社，1990.

[5]皮亚杰.发生认识论原理[M].王宪钿译.北京：商务印书馆，1995.

[6]李文林.数学史概论[M].北京：高等教育出版社，2005.

[7]徐利治.数学美学与文学[J].数学教育学报，2006，15（2）：5-8.

[8]林崇德.学习与发展——中小学生心理能力发展与培养[M].北京：北京师范大学出版社，1999.