极限概念教学的系统分析
2013-11-01付夕联张玉峰
付夕联,张玉峰
(1.山东理工大学 理学院,山东 淄博 255049; 2.中国矿业大学 理学院,江苏 徐州 221116)
1 问题提出
以极限理论为建构基础的微积分是高等院校开设的重要公共基础课程之一,而极限概念的教学一直成为人们讨论的焦点.许多学者从不同角度分析了极限概念教学的困难,并给出了相应的教学建议.文[1]从方法论的角度分析了极限的“ε−N”定义的形成过程,在此基础上,借助于类比方法推出了函数极限的“ε−M”和“ε−δ”定义.文[2]则从潜无限与实无限这对对立统一思想出发剖析了极限概念的实质,并指出传统教学过程中的三点失误.文[3]又从认知心理学的角度对极限概念学习的习得阶段、变式运用阶段以及运用和迁移阶段的认知障碍进行了研究与分析.而文[4]则对学生在初等数学学习阶段接触的无限的知识以及个体无限认识层次做出了分析与调查研究.上述各种观点对极限及其相关理论的教学具有一定的指导意义和参考价值.根据研究者多年来的教学实践及体会,特别是在数学史、数学哲学与数学教育日益密切结合的今天,研究不应单一地从某一侧面对极限概念进行分析,而应以系统化的方法做出全面的分析.首先应从历史演变过程中加强对极限概念的整体认识.其次,要从极限概念的历史发展形成的文化环境中理解极限概念.第三,从极限概念的抽象过程认识其本身的规定性,即要从组成概念整体的要素的相互联系中来把握它的整体结构、功能和性质.也就是说,按照系统论原则,要从极限概念的内部结构和外部联系,从它的存在和发展的来龙去脉以及全部真实关系的总和中加以认识.下文拟从历史的角度分析柯西与外尔斯特拉斯给出的极限定义的特点;明确指出学习极限的“ε−δ”(或“ε−N”)定义的必要性;挖掘其中的文化要素,并指出其教学意义;在此基础上给出极限精确化定义的教学策略.
2 柯西的极限定义
2.1 柯西极限定义产生的背景与过程
关于极限的朴素思想可以追溯到古希腊时代,它与古希腊时代的穷竭法有着思想上的联系.17世纪,牛顿和莱布尼茨利用实无穷小方法创立了微积分,随着微积分在实践中所获得的巨大成功,实无穷观点在这一时期占据了统治地位.但由于对无限思想(实无限和潜无限)认识上的不足,在运算过程中出现了严重的逻辑矛盾,特别是1734年大主教贝克莱在《分析学者,或致一个不信教的数学家.其中审查现代分析的对象、原则与推断是否比之宗教的神秘与信条,构思更为清楚,或推理更为明显》一文中提出了著名的贝克莱悖论,使这一矛盾更加激化,导致了第二次数学危机,使数学家不得不进一步考虑微积分理论基础的建构问题.
在探索微积分理论基础的道路上,拉格朗日、罗依里埃、拉克鲁瓦、达朗贝尔等数学家都付出了艰辛的劳动,尽管没有得到明确的结果,但潜无限思想已开始取代实无限思想,并逐步进入人们的思想.对微积分的重要概念首次作出比较系统而严格叙述的是捷克籍的意大利教士、哲学家和数学家波尔查诺,波尔查诺第一次给出了一个精确的函数连续的定义,沿用至今,并给出了导数的定义.如果把拉格朗日等数学家的工作看成是极限理论的先驱的话,波尔查诺的工作则是向柯西极限理论的过渡.
潜无限完全取代实无限的工作是由法国数学家柯西完成的.柯西于1823到1829年先后发表了3部关于分析学方面的著作《分析教程》、《无穷小计算教程概论》和《微分学计算教程》.这些著作是以严格化为其主要目标的,成为向着数学分析全面严格化的第一步.在《无穷小计算教程概论》的前言中,柯西指出:“我所遵循的方法和其它同类著作中阐述的方法在许多地方是不同的.我的主要目标是想要利用直接考虑无穷小量而产生的简单性来达到严格化,而后者则是我在《分析教程》中为自己规定的信条.”[5]柯西在《分析教程》中,摆脱了与几何图形及几何量的任何牵连,给出了极限的概念:“如果一个变量逐次所取得的值无限趋向于一个定值,最终使这个变量的值与该定值之差要多小就多小,那么该定值就称为所有其他值得极限.”
柯西以这一定义为基础重新定义了使人们感到困惑的无穷小:“如果一个变量这样无限地减小,使其收敛到零,那么我们就说这个变量是无穷小.”从无穷小量出发,柯西重新定义了微积分中一系列重要概念.正是因为如此,柯西被认为是微积分理论基础的奠基人.
2.2 分析与启示
从上述极限概念的历史演变过程可以看出,极限概念是无穷小一般化的结果,即以函数有关无穷小运算的实例为抽象原型,借助于“特性分离一般化原则”[6]抽象出来的.在《分析教程》中,柯西是把无穷小量作为极限的一种特殊情况引出来的,即无穷小是极限概念强抽象的结果.至于无穷小与极限这两个概念之间的区别和联系,柯西在给蒂美尔曼(Timmermans)著的《微积分》写的序言中有过这样一段表述[7]:“人们所采用的讲述无穷小计算(即微积分,calcul infintesimal)的方式是由兰登(Landen)和达朗贝尔(d′Alembert)提出的,并且考虑了极限,这种方法从严格性和准确性来说,比完全缺乏这两点的对手,即无穷小方法具有很大的优越性,因为前种方法只对有限数量应用算术和代数的规则,从而可以掌握其要领;而后一种方法在考虑不能估计大小的数量时,却毫无根据地认为同样的规则一定正确,从而与人们的感觉和理解相违背.因为人们寻求只从极限原理用系统的和统一的方式导出微积分计算的所有命题;但莱布尼茨的老方法在简要和简单方面具有太大的优点,以至于人们不相信能够不讲到它,这就是为什么大部分的重要的证明都有双重证明的原因.一个是为了说服人,另一个是为了使人轻松点,并且加强记忆.当化到极限没有任何困难时,有时甚至于只用无穷小作出一个证明,读者总可以通过思考,使它具有其他证明所采用的更严格的形式.”
尽管无穷小与人们当时对无限的直观理解有一定的差距,但由于无穷小具有明显的简单性和直观性,在微积分发展的初期,无穷小概念主宰着人们的思想.而到了柯西时代,无穷小与极限可以说旗鼓相当,不分优劣,其应用普遍存在.
现行教材中用动态语言描述的极限的定义正是从柯西的极限定义演变而来的.但是“Cauchy在微积分学历史上的地位,不是作为一个同旧传统决裂,清除陈旧的和腐朽的基础来给崭新的和坚固的基础腾出地盘的人,倒有点像承前启后的人物”[8].也许正是由于受到传统观念和思想的影响,在柯西的极限定义中有许多语言是极其模糊的,诸如“无限地趋近”,“要多小就多小”等这些动态语言的表达必然引起人们对运动和量的生成的模糊直觉,使人们不免把柯西的极限定义与芝诺悖论联系在一起,由此难以消除人们对无限理解上的困惑,无法把握极限概念的内在结构.按照数学抽象的基本原则——模式建构形式化原则,即“作为数学抽象物的量化模式在概念意义上就应具有一定层次上的普遍性和概括性,在表述形式上则应具有无歧义的逻辑精确性和简洁性.”[9]柯西的极限定义在内容上已具有一定意义上的普遍性和概括性,但却不具备表达形式上逻辑的精确性.而这正是特性分离一般化原则不可缺少的一个环节,即借助于明确的数学语言来表达分离出来的特性,从这种意义上来讲,柯西只完成了弱抽象的第一步.第二步则是由德国数学家外尔斯特拉斯完成的.
3 外尔斯特拉斯的极限定义及其意义
3.1 外尔斯特拉斯的极限定义
外尔斯特拉斯攻击“一个变量趋于一个极限”的说法,他认为这种说法不幸地使人们想起时间和运动.在他看来,要给出微积分一个严格的基础,必须用静态观念给出极限的定义.
外尔斯特拉斯首先把变量x解释成一个字母,该字母表示数集中的一个数,然后给出了连续变量x的静态定义“如果对某数集中任意一个x0和一系列无论怎么小的δi(i=1,2,…,n),在区间(x0−δi,x0+δi)内总有该数集中另外的值,称x为该数集中的连续变量.函数f(x)在x0点连续的定义是:如果对于任意的一个ε>0,都存在一个δ>0,对于区间(x0−δ,x0+δ)内的所有x,不等式(x)−f<ε恒成立,就说f(x)在x=x0处连续.在这一定义中用A代替f(x0),A就是f(x)当x→x0时的极限.这就是现代极限理论中所使用的“ε−δ”定义.相应地也可以得到数列的“ε−N”定义.
3.2 外尔斯特拉斯的极限定义的意义
首先,极限的“ε−δ”定义是在柯西极限定义的基础上,利用静态观点进一步抽象而得到的.极限概念的形式化定义不仅提供一种证明方法,而且成为分析统一化和一般化的必要工具.在数学史上继欧几里得之后体现数学严格化的又一光辉典范,从而打破在此之前单凭直观、运动去研究某些变量问题的传统方法.其次,该定义的实质在于把有关无限过程问题转化为有限量之间的关系,消除了各种变量极限定义中的无穷小和无穷大的因素,从而回避了极限能否达到的问题,体现出用有限方法处理无限问题的重要思想,这与柯西的极限理论有着本质的区别.柯西的理论建立在潜无限的基础之上,潜无穷小概念是其体系的核心,柯西的概念完成了无穷小分析的发展阶段;而外尔斯特拉斯的理论则以真正的无穷小为基础,在外尔斯特拉斯的体系中,分析实质上变成了一门集合论的学科.第三,由于“ε−δ”语言使用距离来刻画自变量与函数及其所讨论数值的趋近程度的,这种定义形式可以发展为邻域语言或拓扑语言,当它推广为邻域语言之后,在微积分中,许多与正数有关的抽象的理论与证明都可以找到较为直观的几何背景,这对其相关的理论的理解与应用是十分有益的[10].第四,外尔斯特拉斯的极限定义启示人们,在数学活动中,符号化的表述是绝对必须的,因为许多数学对象不能直接地去想象,符号语言不仅仅具有使思维外化和用于交流的简单功能,它对于认知功能和概念化也是不可缺少的.外尔斯特拉斯仅用ε和δ这两个符号刻画出极限概念内在的繁杂结构,也体现出数学家对简洁美、统一美和思辨美的追求.外尔斯特拉斯所给出的极限概念最突出的特征是通过“ε−δ”方法建立整个分析的理论体系.F·克莱因在1895年外尔斯特拉斯八十大寿庆典上谈到那些年分析的进展时说:“我想把所有这些进展概括为一个词:数学的算术化”,而在这方面“外尔斯特拉斯作出了高于一切的贡献”[11].D·希尔伯特认为:“外尔斯特拉斯以其酷爱批判精神和深邃的洞察力,为数学分析建立了坚实的基础.通过澄清极小、函数、导数等概念,他排除了微积分中仍在涌现的各种异议,扫清了关于无穷大和无穷小的各种混乱观念,决定性地克服了起源于无穷大和无穷小概念的困难.今天……分析达到这样和谐、可靠和完美的程度……本质上应归功于外尔斯特拉斯的科学活动.”[12]
“一个传递较多信息的陈述具有更大的价值或逻辑内容,因而它是更好的陈述.一个陈述的内容越丰富,它同我们的目标就越接近,也就是说就越接近‘真理’.”[12]在学习过程中,学生并非仅仅寻求一般的真理,而追求的应该是有益的、有启发性的真理,追求能解答有意义的问题的理论.以动态语言描述的极限定义是直观的,但太空泛太平凡.其次,由于形式逻辑只适用于静态对象的分析,即分析那些含义确定的概念及其关系.如果概念含义变化不居,那么最基本的逻辑规律(如“同一律”)也无法满足,逻辑分析工具便始终无法被协调运用了[13].因此,在动态语言描述的极限定义的基础上也就无法严格地按照演绎方法展开相关的理论了.鉴于这一定义的不足与缺陷以及外尔斯特拉斯极限定义丰富的内涵和意义,讲授极限的“ε−δ”或“ε−N”定义不仅是必要的而且是可行的.
4 概念形成过程中的文化内涵及意义
传统教材以及传统教学法的严重缺陷是学科与学科之间、领域与领域之间的孤立、分割,这个问题从杜威那个时代开始就一直受到批判.从生态学的角度看,知识的综合化、多元化是恢复数学课程内容之间生态关系、在教材内构建完整知识生态系统的重要途径.在这样的生态关系中,知识才能走向“动姿化”.在数学教学过程中,现在亟待需要加强的是数学史和数学哲学.数学教育不能割断历史,更不能脱离历史.数学史不仅能告诉人们数学思想的逻辑行程和历史行程,而且还有助于理解数学学科的社会角色和人文主义.数学哲学则被普遍认为是沟通数学与人文的桥梁,这就需要广泛利用数学史提供丰富生动的素材.研究表明,数学教师是否具有数学哲学、数学方法论、数学史、数学文化等知识储备已成为高效数学教学行为的内因之一[14].有关数学史在数学教育中的作用出现了一系列文章[15~23].概括起来有以下几个方面的作用:(1)有助于认识数学对象的性质和存在方式,形成正确的数学观.(2)考察数学在发展中遇到的障碍有助于解释今天的学生所遇到的困难.(3)有助于激发学生学习数学的热情,培养学生的浓厚兴趣,形成积极的学习态度.(4)历史问题的提出以及数学家解决问题的思考方式,特别是数学家创造性思维活动的过程有助于培养学生的思维.(5)数学史展现出数学知识的人文主义内涵.(6)数学史为教师的教学设计提供一个教学指南.如何充分发挥这些作用有待于研究者在实践中不断地探讨.
4.1 概念中的文化要素
历史是一种文化,它记载着数学思想的发生、发展的形成过程.数学发展是整个人类文化发展的重要组成部分,因此,“数学不应被等同于知识的简单汇集,而应主要地被看成是人类的一种活动,一种以‘数学共同体’为主题、并在一定文化环境中从事的创造性活动.”[24]阐述极限概念的历史发展,并不是原原本本地追寻历史,也不是在教学过程进行简单地移植和嫁接,而是对数学史材料特别是文化要素深入挖掘、提炼、改造和升华,与极限概念教学融合在一起,并在一定的文化环境中展现出来.极限概念的历史演变及形成过程体现的文化要素主要体现在以下几个方面:
(1)历史背景:由无穷小悖论引起了第二次数学危机,数学家开始由实际问题的解决转向微积分理论基础的研究,拉开了分析严格化的序幕.
(2)概念体系:函数连续的定义、函数极限的定义、无穷小与无穷大、数列极限的定义.其核心为极限的ε−语言的描述.按照逻辑建构的顺序,体现出从特殊到一般再到特殊的过程;从历史的角度,则体现出从特殊到一般再到特殊的过程.实际操作的方法则是类比方法.
(3)历史及数学意义:外尔斯特拉斯极限定义的建立是分析严格化的标志;开创了用有限、静态方法研究无限、动态现象的先河.
(4)思想观念:经历了从实无限到潜无限,从动态观念到静态观念的转变.实无限是一个现实的、完成的、存在的整体,即此外永无;而潜无限则永远处在不断构造的进程中,可不断延伸而永无尽头,即此外永有.实无限与潜无限具有与有限的不同本质属性,实无限是一种完成了的实体无限,潜无限是一种突破有限处于不断创生进程中的无限,实无限是潜无限的最终归宿,潜无限是实无限的必要构成,亦即实无限是通过潜无限表现出来的.在历史上的不同时期,实无限与潜无限是此消彼长、相互交替地统治着人们的思想,这从一个侧面说明了二者各具有合理性的客观存在.因此企图以一种无限观代替另一种无限观是不可能实现的[25].对于极限概念,从动态观念到静态观念的转化过程本质上就是从无限转化为有限,即无限的过程应借助于有限量之间特有的结构来揭示.
(5)演进及认知历程:极限概念演进是一个连续不断的过程:由不清晰的模糊概念开始,到它们的逐渐澄清,并达到一个稳定状态.柯西的思维线索按照归纳思维→抽象思维→演绎思维来进行的;外尔斯特拉斯的思维线索则是按照直觉思维→抽象思维→演绎思维而进行的.创造心理历程以辩证分析→观念选择→审美直觉→有用提取→有效组合的心理逻辑展开的.
(6)数学家的生平:坚韧不拔、孜孜不倦地追求真理的一生;柯西对年轻数学家表现出的冷漠与外尔斯特拉斯对后起之秀的热心帮助形成了鲜明的对比,造成了二者晚年精神生活的巨大反差.
(7)人格品质:深厚的数学修养和统一化的数学信念;对传统观念怀疑、批判的态度,合理继承前人成果的包容精神,善于挑战、敢于创新的精神;数学的严格化、简洁美、统一美和思辨美的追求.
4.2 文化驱动极限概念教学的意义
上述要素有机地结合在一起便构成了一个完整的文化系统,以此驱动极限概念的教学有重要意义.首先,中学生的数学观往往是静态的、绝对的、片面的和实用主义的.极限是中学生进入大学后不久就接触的重要概念,这正是处理中学与大学衔接问题的重要阶段,更是有利的时机.微积分的创立结束了古希腊几何学统治数学发展的历史,出现了带有思维创造特征而非直接立足于直观经验的数学对象,这有助于学生正确理解数学对象的演变及来源;而第二次数学危机的出现以及极限概念漫长的建构过程验证了数学发展的曲折性和数学真理的相对性等等.因此,在这一特殊的关键时期,利用极限概念形成过程中广泛的文化要素培养学生正确的数学观无疑是非常重要的.其次,微分学、积分学产生在前、极限理论建立在后,这一历史发展过程体现出逻辑与历史有时是不一致的;在数学发展过程中,先有实践,后建立或完善理论,或先建立理论,后有实践应用都有其合理性.这些史料对于充实课堂教学内容、开阔学生知识视野同样是有益的.第三,“质疑是科学研究的始点,培养创新精神,离不开对学生质疑思维的激发和保护.在我国,质疑思维是重要的,但质疑精神更重要.”[26]从实无限到潜无限,从动态观念到静态观念,无不体现出数学家不畏权威、敢于向传统思想观念进行挑战的勇气,这同样是激发学生质疑思维、培养学生质疑精神的重要素材.第四,极限概念形成过程中涌现出的数学家的崇高的信念、知识结构、思维方式、认知历程、学校教育、治学经验、个性品质以及思想活动特别是创造性思维活动的过程又会成为培养学生数学能力的极具启发性的资源,把这些资源融入到课堂教学中,可以创造一个良好的学习情境,为学生进行创造性的学习奠定了基础.第五,数学学科的教育应该是一种完整教育,既要传授理性知识、培养学生的逻辑思维能力和逻辑实践能力,又要重视培养学生的形成目的和动机能力、灵感和直觉能力、猜测能力、表象能力、幻想能力、情感体验能力等非理性精神能力,以及意向、情感、意志、信念、信仰等非理性精神力量.而非理性精神力量的各种要素的有机结合,便构成一个既对立又统一,又相对稳定并不断变化的极其复杂的动力结构系统,这是一个具有始动、维持、调节、定向多种功能的动力系统,一个能使智慧潜能有效地转化为智慧行为的动力结构系统.认知心理学认为,这种动力是在内外诱因的诱使下内化为一种心理需求,这种需求同一定的目标相结合,就产生了为此目标而努力的动机,激励学生去积极行动.上述有机组合的文化要素为学生提供了丰富的信息资源,直接刺激学生学习过程的心理环境,对学生的理性精神世界和非理性精神世界的形成和发展都会产生积极的影响.
5 概念教学困难的突破
5.1 借助具体数列直观把握极限概念的内在结构
(1)观察、归纳、抽象.观察不同数列变化的趋势,归纳其共有性质,抽象出极限如下的定义:如果当n无限增大时,an无限趋近于某一确定的常数a,则称a为数列{an}当n→∞时的极限.这一概念无疑是抽象思维的产物.马克思指出:“在人类认识过程中存在着两条方向相反的道路,在第一条道路上,完整的表象蒸发为抽象的规定;在第二条道路上,抽象的规定在思维的过程中导致具体的再现.”[27]这也就是说,在这两条相互连结的道路上,认识开始由感性的具体表象通过思维活动分析出各种单向的、孤立的抽象规定;尔后,这些单向的、孤立的抽象规定又在思维的行动中被连结起来,综合成思维的具体再现出来.这一过程中,认识必须经历感性具体、概念的抽象规定和概念在思维中的具体3种状态.感性具体又指概念的感性映象,即通过感觉、知觉形成对常识性材料的初步心理表征,具有直接性、生动性和具体性的特点,是连接人的意识和外部世界的通道.抽象规定是从事物整体中抽取出来的个别成分.它包括两个阶段:即经过初级抽象得到的单纯知性的抽象规定,这是抽象的一般.再经过高级抽象得到理性的规定,其内部包含着若干要素的关联耦合或辩证矛盾,这是具体的一般.在上述定义中,体现出双重对应变化关系:对每一个确定的正整数n都唯一地对应着一个有限常量an,当n变化时,an是变化的;当n无限增大时,an无限趋近于某一个确定的常量a.而在n无限增大的过程中,依次取1,2,3,…,n所得到的一列数a1,a2,…,an体现出an的无限变化过程,蕴含着潜无限思想,数列{an}无法真实地写出,该定义就无法暴露其内部要素n、an及a之间的耦合关系,也就是说不可能达到极限概念最深层的矛盾结构,也就无法理解“an无限地趋近于某一确定的常数a”的本质含义.因此上述定义从认识过程来看只能属于抽象规定的第一个阶段,即抽象的一般,必须进行进一步的高级抽象才能使其上升到具体的一般.
(2)由抽象到具体,化一般为特殊.按照历史相似性理论,学生对于学习难点的理解以及转化过程与历史存在相似性.数学家在创造过程中遇到的困难或出现的错误,在学生身上也会重新发生.因此回顾数学知识的历史、分析数学家在做出创造时的失败与挫折对于预见、解释学生的认知困难有着极强的启发效果.极限概念教学难点的突破本质上就是思想观念的突破,这与极限概念的历史发展是一致的.按照徐利治先生所创立的抽象度分析理论[28],小难度和中难度的抽象思维适用于已有理论的补充与完善,而大难度和特大难度的抽象思维则往往适用于新概念或新理论的创立,需要人们改变以往传统观念,引起思想上的质的飞跃.从历史角度可以看出,柯西与外尔斯特拉斯所给出的极限概念至少具有大难度.在教学过程中,如何把体现潜无限思想的无限过程转化为有限量的关系也就成为极限概念的动态描述转化为静态刻画的一个主要环节.
化难为易、化繁为简、化抽象为具体、化一般为特殊(或化特殊为一般)等都是学习过程中经常使用的化归方法.可以选择具体数列如
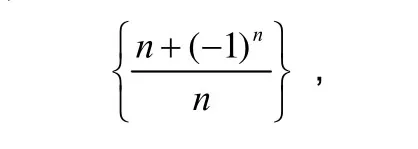
显然,当n→∞时,
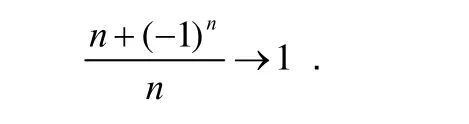
又可以转化为当n→∞时,
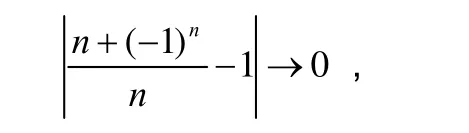
即当n→∞时,→0.这实质上把数列
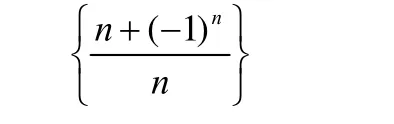
(3)试验分析,直观把握.对数学概念真正的理解、真正的懂离不开数学直观.徐利治先生指出:“只有把它理解的非常自然,非常直观,直至成为你心目中一目了然的东西,那才真正变成你自己的知识财富,这时候,你就能使用自己的语言很自然地而不是背诵式地去表述你所理解的一切.”[29]取一系列的很小的数ε1,ε2,…,εk等,由以上分析有

于是得到相应地N1,N2,…,Nk,使得当n>Ni(i=1,2,…,k)时,必有

在数轴上作出以原点为中心的εi(i=ε1,ε2,…,εk)邻域,则在该邻域内包含了从
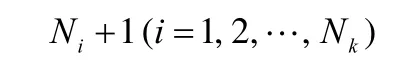
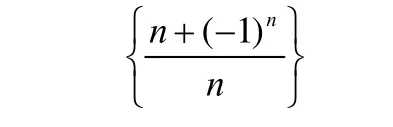
中满足n>N的所有项都落在1的ε邻域内.也就是对任意的正数ε,都能找到正整数N,对满足n>N的一切n,都有
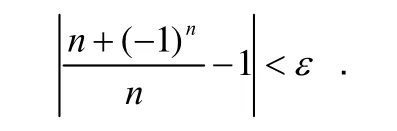
由上述特殊数列的极限定义的直观理解,不难得出当n→ ∞时,an→a的“ε−N”定义.有了数列极限的定义,可以借助于类比法推出函数极限等的精确化的定义,文[1]给出的建议值得借鉴.
5.2 由连续函数的几何图形直观把握极限概念的本质
考察极限概念的发展历史,既要把握极限概念的整体演变历程,又要分析数学家的具体认识过程.1799年,为了给出代数基本定理的一个单从算术、代数和分析相结合的证明,波尔查诺首先阐明函数连续性的定义,第一次明确指出连续观念的基础存在于极限之中.而外尔斯特拉斯同样先给出了函数在某一点连续的精确定义.函数的整体连续性具有现实原型的,与学生的实际生活密切相关的,在某一区间上的连续函数就是一条连续不断的曲线,具有相当明显的直观性.M·克莱因指出,任何一门学科最初都是通过直观方法建立的,每一位数学家都是直观地思考问题,然后才用演绎形式表达结论.所以数学理解是通过直观方法获得的,逻辑表达不过是学习的辅助工具[30].受此启发,在极限概念的教学设计中,以函数f(x)在区间I上的整体连续性为突破口,直观地观察到x→x0时,f(x)无限趋近于f(x0)的.亦即当x→x0时,(x)−f(x0→0;也就是(x)−f(x0可以做到足够的小,只要x与x0足够接近.再次借助于直观,作出直线
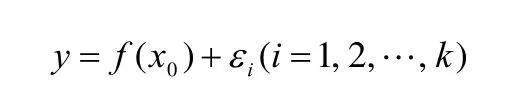
和
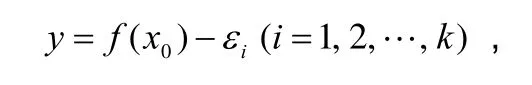
则可以得到

直观地可以找出相应的δi(i=1,2,…,k),极限的本质暴露无遗.再按照类比法推出一般函数极限的定义,最后得到数列极限的定义,这也不失为一条有效的教学策略.
6 极限定义内在规定性的辩证分析
极限定义中包含着丰富的辩证法,如ε的任意与确定的二重性、N的存在性与不唯一性,ε与N决定与被决定的关系、极限定义中常量与变量、过程与结果、精确与近似的对立统一关系等内容的挖掘对丰富学生的知识、进一步理解极限的定义无疑是有意义的,在此就不再赘述.
[1]常瑞玲.用数学方法论指导极限概念教学的尝试[J].数学教育学报,2000,9(1):78–80.
[2]顾光辉,吕朝阳.实无限与潜无限视角下的极限概念[J].数学教育学报,2004,13(3):66–67.
[3]李莉,谢琳.关于学习极限概念认知障碍的研究与分析[J].数学教育学报,2006,15(1):42–44.
[4]张卫平.文科学生学习微积分前对无限的认识层次分析[J].数学教育学报,2006,15(3):54–57.
[5]爱德华.微积分发展史[M].张鸿林译.北京:北京出版社,1987.
[6]徐利治,朱梧槚,郑毓信.数学方法论教程[M].南京:江苏出版社,1992.
[7]李家宏.关于无穷小概念的历史注记[J].自然科学史研究,1998,17(2):129–138.
[8]戈登·迈·菲希尔.柯西和无穷小[M].郭书春译.上海:上海科技出版社,1985.
[9]徐利治,朱梧槚,郑毓信.数学方法论教程[M].南京:江苏出版社,1992.
[10]李莉,谢琳,王诗云.关于两种极限定义方式在教学中的比较[J].数学教育学报,2002,11(4):31–33.
[11]吴文俊.世界著名数学家传记[M].北京:科学出版社,1995.
[12]波普尔.客观知识[M].舒伟光,卓如飞,周柏乔,等译.上海:上海译文出版社,1987.
[13]谢琳,战玲.极限概念的意义与数学发展的语言转向[J].数学教育学报,2010,19(5):90–92.
[14]王光明.高效数学教学行为的归因[J].数学教育学报,2010,19(5):75–79.
[15]汪晓勤,林永伟.古为今用:美国学者眼中数学史的教育价值[J].自然辩证法研究,2004,20(6):73–77.
[16]王青建.数学史:丛书斋到课堂[J].自然科学史研究,2004,23(2):148–154.
[17]薛红霞.在数学教学中渗透数学史的作用[J].教育理论与实践,2005,25(12):40–42.
[18]杨宝珊,杨刚.于数学史与数学教育思维研究[J].西北大学学报,2005,35(5):657–660.
[19]张维忠.传统与数学教育现代化[J].教育研究,2005,(8):36–41.
[20]张楠,罗增儒.对数学史与数学教育的思考[J].数学教育学报,2006,15(3):72–75.
[21]沈南山,黄翔.明理、哲思、求真:数学史教育价值三重性[J].西南大学学报,2010,36(3):141–145.
[22]杨渭清.数学史在数学教育中的教育价值[J].数学教育学报,2009,18(4):31–33.
[23]徐利治,王前.数学哲学、数学史与数学教育的结合——数学教育改革的一个重要方向[J].数学教育学报,1994,3(1):3–8.
[24]郑毓信,王宪昌,蔡仲.数学文化学[M].成都:四川教育出版社,2000.
[25]杜国平.潜无穷、实无穷探析[J].自然辩证法通讯,2009,181(3):18–25.
[26]王光明.数学教育需要重视的两个问题[J].数学教育学报,2005,14(1):31–33.
[27]马克思,恩格斯.《马克思、恩格斯》选集(第二卷)[M].北京:人民出版社,1975.
[28]徐利治,郑毓信.数学抽象方法与抽象度分析法[M].南京:江苏教育出版社,1990.
[29]徐利治.漫谈数学的学习和研究方法[M].大连:大连理工大学出版社,1989.
[30]汪晓勤,张小明.HPM研究的内容与方法[J].数学教育学报,2006,15(1):16–18.
