试论数学文化视域中的数学学习

徐文彬

（南京师范大学 课程与教学研究所，江苏 南京 210097）

数学学习，在小学生们的眼里大多就是计算，即便是所谓的应用题也不过是把其中的“数量关系”转变成计算的式子，最后给出计算的结果，并附上“必不可少的”“答：……”，即使是现在一年级就有的“统计内容”也是少不了要“数数”，而几何知识则更是变成了“点、线段的个数，边长、周长和面积的计算”.在初中生们的心里，几何学习就是要给明白无误的“定理、性质、公式和规则”找出各种各样的理由，以形成所谓的“证明”，而代数学学习则是要记住一大堆原理、规则和公式，然后就是把它们应用于解决“多如牛毛、怎么也做不完”的习题当中去.而高中生的数学学习则由于“高考压力”的存在更不待言……之所以会造成上述所描述的“普遍现象”，研究者认为主要是由于“数学科学教学（论）”忽视了基于“数学文化”[1～2]视域分析下数学创造、发明与学习中普遍存在的游戏性、流变性和融贯性.

1 数学学习的游戏性

游戏有“有待之游和无待之游.有待是有所依靠的，无待是无所依靠的”[3].但学校（数学）学习，如所周知，它必是“有待的”，至于是否游戏则需另议.另一方面，游戏“始终被理解为其自身之外没有其它任何根据的活动”[3].而学校（数学）学习却不仅“有所根据”，而且还有着众多的“根据”.由此看来，要使学校数学学习成为“游戏”尤其是“无待之游”恐怕有点勉为其难.但这只是学校数学学习的一个方面的特点，而如果能够从数学文化的内在尺度来分析学校数学学习，那么就很可能会得出一些“相反的”看法或结论.

数学在古代中西方传统中都充满着一些游戏的味道.譬如，算术数论之中像“完全数”、“亲和数”、“孪生素数”等概念的提出和对它们的研究就是“游戏中的事情”；几何中的“三大作图问题”更是古希腊人“茶余饭后”的游戏活动.甚至可以说，“数学只是古希腊人的一个高级玩具，而非一个有用的工具”[4].出现于《张丘建算经》中的“百鸡问题”（即“今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一.凡百钱买鸡百只，问鸡翁母雏各几何？”）可谓也是一个“数学游戏”中的上品.

爱因斯坦曾说：“许多人爱好科学，是因为科学给了他们异乎寻常的智力上的快感.对于这些人科学是一种特殊的娱乐；还有许多人之所以把他们的智力奉献给科学祭坛，为的是纯粹的功利.如果把这两类人都赶出神圣的殿堂，那么，这里的人就会大为减少……”[4]由此可以想见，现代的学校数学教育存在着要把学生都赶往为“纯粹的功利”而学习数学的轨道上去的危机.执着于数学的“纯粹的功利”是现代数学教育的一个“顽固的症结”，必须用“游戏的精神”才有可能加以稀释乃至根除.

从总体上来说，（纯粹）数学就是人类“前赴后继的”游戏精神的创造物.希尔伯特的“有限数学”计划就是想探明“数学游戏”的所有“有待的”根据，而歌德尔的“不完全性定理”则表明，数学从总体上来说，是一个犹如德里达所说的“无底棋盘上的游戏”一样，是一个“无待之游”.也就是说，数学的绝对真理是不可企求的，而它的相对真理则是“边界内的游戏”或“有底棋盘上的游戏”，自由但“有待”.维特根斯坦则从“语言游戏”的角度对数学的“游戏”本性进行了分析：“数学是特殊的，但其特殊性不在于它拥有比人类其它活动更高贵的特权，而只在于它是一种特殊的语言游戏.”但“‘一个数学命题的理解不能像大多数非数学命题那样，由它的词语形式来保证’.也就是说，在其它许多语言游戏中，词的理解可能有关键的意义，而在数学中，词只在关系中意义才凸现出来，由此，‘在数学中，一般与特殊的关系与在其它地方的这种关系是不同的’.因而，证明才在古往今来的几乎所有数学中占据决定性的位置.”因此，“数学也仅只作为诸多语言游戏、语言模式之一种而有其独立的存在.这样，它就不再位于生活之外或之上，而是在生活之中.”[5]

由此可见，根植于“数学文化”的（学校）数学教育就应该重视通过游戏来促进学生对数学的学习.如果说“无待之游”的数学游戏比较超然，而不易于被引进学校数学学习当中的话，那么，“有待之游”的数学游戏则必然是现实可行的绝好学习活动：“唤醒学生的最好的办法是向他们提供有吸引力的数学游戏、智力题、魔术、笑话、悖论、打油诗或那些呆板的教师认为无意义而避开的其它东西.”（马丁·加德纳语）[4]

如此而来的结果可能就是，如果从“数学游戏”的角度来看待小学数学中的“计算”学习，那么，“计算”就只不过是整数运算规律下的“数字游戏”而已.而这里的运算规律则也只是“十进制下的”加法的结合律和交换律、乘法的结合律和交换律、乘法对加法的分配律——即“数字游戏”的规则.因此，在学生学会基本的自然数知识与简单计算技能的基础上，有关“自然数的四则混合运算”的学习就完全可以成为学生自己的“游戏活动”——类似于幼儿的“积木”游戏.而以上述“运算规律”为基础的一系列导出规则——类似于“积木组块”，也就必然会成为他们玩“数字游戏”的自由探索之所得.因此，还需要用原计划的“8个课时”来“按部就班”地施教或学习吗？研究者曾通过在一个班级的实验发现，学生只需要3～4个课时的时间就可以完全独立、自主地探索出“导出规则”，并能够运用它们和基本运算规律一起来解决“计算问题”.而余下的4～5个课时的时间则用可来拓展二进制、八进制、十六进制等“规则”下的“整数的计算”游戏活动.通过这样的处理之后，可以发现，学生们可以隐约体会到：他们所学习的整数的计算不过是“整数”在一种“规定的”特殊进制（即十进制）下的“必然结果”，而且还存在着许多这样“规定的”特殊进制下的“运算规律”及其必然结果.所以，通常所说的“1+1=2”实际上就是省略掉了“十进制”这样一类“规定”而得自于“文化”的“约定限制”的必然结论，并因此而被认为是理所当然的“数学事实”，无须质疑.可以说，如果没有这样一类文化的约定限制，那么，人们的生活将会毫无着落，虚幻而不可捉摸.但是，发明创造却要在某种程度打破这种文化的约定限制，否则，进步就将会成为“不可能事件”.众所周知，中国的《周易》中就蕴藏着“二进制”思想，但发明二进制的人却不是中国人，而是与牛顿一同发明微积分的德国数学家、哲学家G·W·莱布尼茨（Leibniz，1789—1857）.为什么会出现这种情况呢？这难道还不值得深思吗？

其实，就是高中生的数学学习也存在着类似的问题[6].譬如，无论是在传统综合几何思想指导中，还是在现行“向量几何”思想指导下的“空间两条直线的位置关系”的学习，都没有摆脱“共面与异面”（所谓两条直线“异面”就是指，无论如何，这两条直线都不可能同在某一个平面内；而所谓两条直线“共面”则是指，无论如何，这两条直线都可以同在某一个平面内，而共面又可分为“平行”与“相交”）这一传统的分类或区分.但事实上，如果能够运用综合的“数学文化”观下的整体思想与“平移运动”于数学学习的指导当中，学生就很有可能发现另一种分类或区分：“重合与相交”.所谓“重合”就是指，在“平移运动”下能够完全“重叠”的两条直线，而所谓“相交”则是指，在“平移运动”下不能够完全“重叠”的两条直线（因而只有一个“交点”），而“相交”则又可分为“共面的相交”与“异面的相交”；更为重要的是，数学中的“转换/转化”思想在此体现无疑：不论是在综合几何还是在“向量几何”当中，有关“异面”的问题解决总是要转换/转化为“共面的相交”来思考.由此可见，“共面的相交”与“异面的相交”之间存在着诸多共性，故，依此“共性”可以归为一类矣！

2 数学学习的流变性

流变性主要来自数学文化的整体性和统一性，也来自儿童的整体性和统一性.“流变”可以说是世界存在的基本形式，也是世界普遍联系和永恒发展的必由之路.

当代数学文化发展的整体特征之一便是它的整体性与统一性.尽管数学文化的各学科之专业化和职业化对这整体性与统一性潜藏着“割裂”的危害，但综合的“数学文化”观却既是为克服这“割裂”而又不完全排除“专业化和职业化”所做出的努力.近年来，由于高考与就业压力的增大和“望子成龙”或“望女成凤”这一怎么也挥之不去的“育儿成才”或“教学成才”情节之原由，在某些高中甚至喊出了“一步到位”的主张，而在某些小学则甚至从二、三年级就开始以“奥数”为标准而把学生分成“三、六、九等”以为“因材施教”铺平道路.不论是“一步到位”还是“因材施教”，其实都是违背儿童或学生的整体性和统一性之流变的“强硬”态度之反映.且不说，在“数学学习”中概念的含义只有在关系中才能显现出来，就儿童学习数学时的“整体投入”而言，他们也不可能在数学课堂上只能“数学地思维”，更不用说，在算术课上只能运用“计算程序或步骤”来“算术地”思考.所以，流变性应该是数学学习的一个“天然的”特性，而不是像“数学科学教学论”所认为的那样：这是注意力不集中的表现.下面便是一个来自“幼儿园”的观察，应该很能够说明该问题之所在：

背景：一位数学教师（幼儿园阿姨）和4位5岁左右的儿童在上“5的认识与书写”一课，其重点是“正确地”书写“5”而不是认识“5”，因为“对5的认识”对于5岁左右的儿童来说早已不成问题.“男生”中有一位是加拿大华侨，很独立且“自私”（记为“A”），还有两位是中国人，其中有一位被老师认为“有点笨”（记为“B”，另一位记为“C”）；还有一位“女生”（记为“D”），来自韩国，不会说汉语.该教师还兼教小学二年级一个班的数学课，不会说韩语.上课时间为40分钟.上课地点为儿童活动室.

上课：每位学生面前放着一个方格本，上面记录着“学生的数学成长痕迹”——1、2、3、4的书写，老师讲解黑板上早已在上课前“写好”的一排方格中的“5”.讲解完后，教师请同学们在自己的方格本上照着黑板上的样子.写一页“5”（有近50个方格）.老师则看着“学生们”写，并不停地“手把手地”认真地指点着学生.“老师”，A说话了：“D在地上爬，她还抠墙上的‘地板模’.”“老师”，B也说话了：“A不把橡皮给我.”“这是我的，就不给.”A说.老师对他说，同学之间要互相帮助，但没有丝毫“作用”.A好奇地瞪着两只大眼睛看着老师，也不说话.“还是用我的吧！”C好心也是“讨好地”说.“老师，我们喝奶吧？”这时牛奶已经送到了教室门口.正感无赖的老师闻之一惊，“机智地”抓住了这个“教育机遇”：“谁先写完就喝奶.”于是，学生们在牛奶的诱惑下“认真地”完成了这一节课的教学任务，老师还当堂给予了同样是“认真的”批阅.牛奶喝完后，学生们却各自专心地玩起了自己的游戏.D在这节课上还有一个意外的收获，那就是学会了说：“wu”……

课后：老师感叹：“教他们还真不如教二年级的学生，B还总是忘记带‘东西’，真苯！”“A很聪明，但很自私，他的什么东西都不让人动.”“D不会说汉语，可费劲了！”“不这么教不行，否则到一年级他们就不会‘写（数）’，家长和老师还会怪我们呢！”……

这里，研究者丝毫未见算术中数的整体性和统一性：“按照传统的教学方法行事，10以内的每一个数是单个地学习的.学习每一个数都要花费相当多的时间，而且，数是应用在各种事物上出现的，后一个数的学习，联系前一个数.例如，3这个数被说成是2和1两个数组成的.以后的每一个数也都是这样来学习.这里似乎有着后一个数和前一个数的联系.这在某种程度上确实如此.可是，这种联系是狭窄的和片面的，因为从1～10的整个数列，作为某种统一的整体，完全没有提到.”[7]而儿童的“数学学习的”流变性倒是被注意到了，但却被视为是“影响正常教学的不利因素”.

其实，不仅如此，就是在算术和代数之间也存在着内在的、统一的整体性.尽管现行数学课程标准把“数与代数”合并成一个内容标准（据说，这也是一种“国际接轨”，因为在美国和英国就都是把“数与代数”作为一个“整体”而构成其数学课程标准或教学标准的一个课程或教学目标），但是，“代数”（即“式与方程”）却只是在第二学段（4～6年级）偶尔“以算术的形式”出现，而“代数思维”（即“数与式”、“方程与不等式”、“函数”等）则只有到了第三学段（7～9年级）才会大量地涌现.应该说，这种想法有其可取之处，但现实的学校数学学习却并不是这么回事.即使学生在学习算术时自发地流变出“代数思维”的创造，也会被视为“不正常”而遭受漠视，以至被扼杀.譬如，当一个二年级的小学生“正在”说计算“71-54=?”的过程：“70减去50得20，4减1得3，20减3得17就是答案”时，甚至在学生还没有说完的情况下，老师就迫不及待地好心“引导”：这样不对，还是想想别的办法吧！

为什么会出现这种“反教育”的教学现象呢？研究者可以负责任地说，出现这种现象的主要原因不在教师方面，而在教材的体系结构和“数学科学教学论”、甚至数学学习（科学）心理学研究方面.首先，就教材的体系结构而言，已有研究表明：不同的教材体系结构影响小学生的数学认知发展[8].其次，就“数学科学教学论”研究而言，它不仅存在着自身不可克服的内在困境，而且，在现实的研究当中，幼儿数学学习、小学生数学学习和初中生数学学习（就更不用说高中生数学学习了）的教学研究是一个割裂的、由不同人群各自研究、鲜有纵向联系和合作的一个“部类”.就数学学习（科学）心理学研究而言，“由于心理学家研究数学学习时，可能由于自身数学知识结构的关系，在数学知识选材时广度和深度就要受到限制，研究难以反映数学学习的全貌.”[9]

这位小学生的“说”当中隐藏着“代数思维”：71-54=(70-50)-(4-1)＝17，或者，更为一般地有，ab-cd=(10a-10c)-(b-d).前者在小学数学中常常被称为“巧算或速算”，而体现在低年级的“奥数”当中，而后者则常常是高年级的“奥数”内容.显然，在小学二年级教师不可能教授后者（这是“代数”），甚至也不可能在现有的教材体系下传授前者，但是，那种“未完成”的“说”却是允许的，也是值得肯定和鼓励的.其实，就前者而言，在改造教材体系之后也不是不可能的普遍事情.而这“说”和类似“71-54=(70-50)-(4-1)=17”这样的式子（譬如，71-54=71-60+6=17）就是所谓的“准变量思维”和“准变量表达式”.它们的存在说明，可以在小学数学教育中进行“代数学习”.因为“算术和代数之间的人为割裂不仅剥夺了学生在小学低年级思考数学的有效图式，而且这还给他们在后续学习代数时造成了更大的困难”[10].所以，为了理解和运用算术中的“代数思维”来促进学生的数学学习，小学数学教师尤其需要培养“代数的耳朵和眼睛”[11].在“代数的耳朵和眼睛”的倾听和透视下，算术之中就会充满着流变的“关系和变量”.由此看来，所谓小学“奥数”并不像人们通常所认为的那样“深奥难懂”，只能为少数具有“数学天分”的学生所独享，而且，在用“代数的耳朵和眼睛”改造后的小学数学学习当中，“奥数”就应该而且也可以成为更多学生的“家常便饭”.

3 数学学习的融贯性

融贯性是指整体和统一的儿童投身于同样是整体和统一的数学文化（学习）当中所应该而且也能够感悟到的数学文化的“内在一致性”.它需要以“游戏性”和“流变性”为其存在的先决条件.如果说数学学习的“游戏性”和“流变性”是“综合文化数学观”下数学学习所应该具有的基本特性的话，那么，数学学习的“融贯性”则就应该是“综合数学文化观”所应追求的一种“超越”有限规则，并体验“无限”规则的创造或自由.

与当代数学文化发展的整体性和统一性特征相伴而生的是数学各学科研究的专门化趋势.而这种“专门化趋势”的发展却也存在着可能的危害，即，在这个崇尚制作，人人都忙于自己的制作，以致于制作产品是否有意义或是否隐藏着谬误却已是无人问津了的“后现代”“社会—文化”氛围当中.数学家和数学工作者的数学研究也存在着“制作的表现”：空洞性——为获得特定结论而有意设置条件以致形成条件堆砌下的一具空壳；雕砌性——随意对一种数学理论进行改造，精雕细琢以构建新理论，即“无聊和无关紧要的理论的形式发展”；批量性——在如同社会上广为流行的“写作秘诀”、“作文大全”、“谈判技巧”和“人生指南”一样的“数学作文法”指导下批量生产或复制“数学研究”论文[12].数学研究中的这种“制作风尚”显而易见是数学教学（研究）所不能解决的一个“大问题”.但是，“综合数学文化观”在数学教学（研究）中的贯彻却要求研究者应以“超越的眼光”来过滤这“有限规则的游戏”，以寻求“无限规则的自由”.

譬如，在智商测试和“探索规律”数学学习中经常出现的“按规律填数字”就既能够说明这“规律”的“制作性”，又能够表明这“规律”也可以成为“无待之游”中的“待”——从游戏的角度来看；也可以成为一切“变化规律”中的“总规律”——从“流变性”角度来看.下面看两个具体的“按规律填数字”的例子.

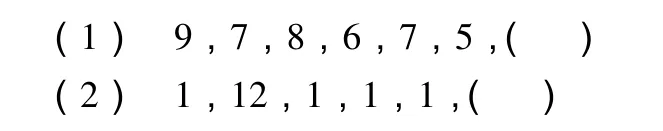
在一本专讲“创造性”的书[13]中是这样分析的：就第一小题而言，“大家都知道括号内应该填6，即按照减2加1的规律.”——你知道“减2加1”是什么规律吗？就第二小题而言，“如果仅仅从抽象的数字符号想下去很难有结果，但只要跳出去，越过它的一般属性去联想，就豁然开朗，答案是2.”——知道了“答案是2”，可还是不知道这“规律”是什么？“生活中我们都见过挂钟，它在整点时几点打几下，半点时都是只响一下.原来是从11点半到下午2点的排列.”——“性质跃迁”式的创造性思维的重要形式之一.

其实，如果研究者对“规律”做一简单的分析，就会知道，所谓“规律”它必定是时间的函数，是变化中的“不变”，是历史、过程、经历的“痕迹”，它还是未来时间里的“变化趋势”.因此，就可以就“未来”来“制作”规律.

就第一小题来说，“减2加1”可能是指：……，?=(7-2)+1，而5=6-2+1、7=8-2+1、6=7-2+1、8=(9-2)+1，至于前面的两个数7和9，如果它们前面还有数字的话，就可以把这“减2加1”的规律向前续下去——7＝(8?-2)+1、9=(10?-2)+1、……于是，就得到了一个符合“减2加1”规律的“无穷数列”：

……，10，8，9，7，8，6，7，5，6，……

就第一题而言，“减2加1”还可能是指：……，7=9-2，8=7+1，6=8-2，7=6+1，5=7-2，?=5+1，至于前面9，如果它前面还有数字的话，就可以把这“减2加1”的规律向前续下去——9=8?+1、8=(10?-2)、……于是，就得到了一个符合“减2加1”规律的“无穷数列”：

……，10，8，9，7，8，6，7，5，6，……

……

如此而言，难道下面的“无穷数列”不也是“一系列规律”吗？而且还很“优美”——周期性变化，犹如一年四季——“春有百花秋有月，夏有凉风冬有雪.”

……，a/x，9，7，8，6，7，5，a/x，9，7，8，6，7，5，a/x，……

由此可见，“减2加1”规律的“制作性”，以及“a/x”的“制作性”和“超越性”的统一.如果认为仅此（即“9，7，8，6，7，5，6”）而已，“前无古人，后无来者”，那么，暂且不说这“规律”无以成为规律——因为“规律”来自人们对无穷或无法把握的世界的人类“心灵的”、“共同的”“约定”或“认定”或“信仰”——“仅此而已”无须“规律”就已一览无余，倒是这“仅此而已”反而更说明了这“减2加1”规律的“制作性”特点或特征.

就第二个小题而言，完全可以模仿第一小题来制作“周期性规律”.当然，前面的“答案规律”跳出了“抽象的数字符号”而获得了某种“生活的意义”.但是，那周期性规律难道还不能成为“最大的”生活意义吗？——谁又能逃脱这“周而复始”的“周期性循环”呢？

不仅如上所言，而且，那括号内的数字可以填下你所能想象得到或无法想象得到、或者你所喜欢或不喜欢的任何“数”.只要你填上了，就可以从“抽象的数字符号”的角度来“制作”“合身的”规律——这难道不也是一种“生活的意义”吗？——数学学习为什么不能进入这无穷的创造天地呢？

其实，在数学各科的学习当中都存在着这片“无穷的创造天地”，而这各学科的“无穷创造天地”之间的“沟通”所形成的“无穷创造天地”将是无法用语言来描述的“无待之游”.由此看来，制作并不是什么可怕的东西或活动，重要的是要以“一以贯之”的精神去制作，并以“一以贯之”的精神去研究这制成品，以形成……

譬如，在初中平面几何的学习当中，就“四边形”这一单元而言，学生们不仅在此前学习了三角形等，而且在此中还要学习各种“规整”四边形：正方形（正四边形）、长方形（矩形）、菱形、鸢形（针形）、梯形、直角梯形、等腰梯形、平行四边形、……、一般四边形.一般的教材都是从平行四边形入手来组织学生的学习，然后再把从幼儿园就开始学习的正方形和长方形纳入到这里的体系当中，接着就是其它四边形的逐个学习，在这个过程结束后，学生们几乎完全忘记了最开始所被给予的“一般四边形的定义”：请他们画出一个四边形时，几乎都是已学过的某一种特殊的四边形.其实，在这里，为了追求数学学习的融贯性，完全可以让学生们从任何一个“特殊的四边形”甚至三角形“出发”，来展开自己的“四边形学习”.不仅如此，而且还可以在此基础上把三角形、四边形和其它多边形甚至“圆周”和“空间图形”等统一起来，在图形、性质、公式等几个方面形成更大范围的统一的融贯性.

当然，以上所描述的数学文化视域中的数学学习首先需要数学教师们自己去这样来学习数学或看待数学学习，以体会其游戏性、流变性和融贯性.否则，没有“一以贯之”的身体力行就不可能带来同样是“一以贯之”的数学文化的学习.正所谓“要想教他人学习，就得首先自己学会学习”.

[1]谭晓泽.古希腊数学文化的精神遗产及其教育价值——以毕达哥拉斯为中心的考察[J].数学教育学报，2010，19（2）：27-29.

[2]徐乃楠，刘鹏飞，王宪昌.中国数学文化发展与数学文化学构建[J].数学教育学报，2011，20（2）：4-9.

[3]彭富春.说游戏说[J].哲学研究，2003，（2）：39-45.

[4]王幼军.数学中的游戏因素及其对于数学的影响[J].自然辩证法通讯，2002，（2）：12-17.

[5]叶闯.数学：一种特殊的语言游戏——评维特根斯坦后期数学哲学[J].自然辩证法通讯，1992，（4）：26-32.

[6]陈克胜，代钦.融入还是包容——关于《普通高中数学课程标准（实验）》中的“数学文化”的思考[J].数学教育学报，2011，20（5）：90-92.

[7]Л.В.赞可夫.论小学教学[M].北京：教育科学出版社，2001.

[8]何纪全.关于小学生对应用题结构认知发展的初步研究（Ⅰ）[J].心理学报，1988，（1）：8-14.

[9]徐速.国内数学学习心理研究的综述[J].心理科学，2003，（5）：877-881.

[10]Carpenter T P, Levi L.Developing Conceptions of Algebraic Reasoning in the Primary Grades [C].Paper Presented at the Annual Meeting of American Educational Research Association, Montreal, Canada, 1999.

[11]Blanton M, Kaput J J.Algebraifying the Elementary Mathematics Experience PartII: Transforming Practice on a District-wide Scale [A].In: Chick H, Stacey K, Vincent J, et al.Proceedings of the 12thICMI Study Conference [C].The Future of the Teaching and Learning of Algebra.Melbourne: University of Melbourne.2001.

[12]黄力民.后现代文化思潮在数学中的影响[J].社会科学战线，2000，（5）：56-63.

[13]王健.创新启示录：超越性思维[M].上海：复旦大学出版社，2003.