大学生对微分概念的理解及认知方式分析

高雪芬，鲍建生

（1.浙江理工大学 数学系，浙江 杭州 310018；2.华东师范大学 数学系，上海 200241）

1 问题提出

历史上，微分是一个非常重要的概念，微分学有两类基本问题：变化率问题与增量问题.为了研究前者，引进了导数概念；为了研究后者，引入了微分概念.而当前高等数学教材[1]中一般是先讲导数，再讲微分，并且微分所占的篇幅较少，所以学生常常认为只要掌握好导数的概念和算法，就可以进行微分的运算，从而忽视了微分概念的学习.如果学生对微分概念没有理解，也就无法对导数、积分等重要概念及其间的关系有深入的认识，更无法掌握微积分思想的精髓.

近年来，各国出现了一些与微积分概念有关的研究.如以色列的Ivy Kidron[2]和西班牙的Joaquim Barbé[3]等人对“极限”概念理解的讨论，英国的Erhan Bingolbali[4]、美国的Ed Dubinsky[5]对导数概念理解的研究等.研究表明，很多学生对连续性、可导性、二阶导数等缺乏正确的理解[6].一些学生对极限、连续、导数的概念意象是片面的、冲突的、甚至是缺乏的，不理解它们两两之间的联系[7].微分尤其是全微分的概念较为抽象，学生往往理解不透[8].纵观现有文献，主要有以下特征及问题：对极限和导数的研究居多，对微分的研究很少；对一元微积分的研究居多，对多元的很少；对于学生的学习困难以经验型的描述居多（如文[8]）而科学系统地分析的较少；鲜有文献论及大学生对全微分及偏导数系列概念的理解情况.故而，研究者以微分概念为核心对学生进行了测试与访谈，研究了大学生对微分概念的理解情况，并分析了关于微分的概念误解及学生的认知方式，指出学生对概念的理解和其认知方式的关系，提出了相应的教学建议.

2 研究方法

2.1 研究对象

主要采用目的抽样选取研究参与者.在综合考虑了学生的专业、任课教师、学习成绩后，选取了浙江省一所综合性大学5个专业的10名大一学生作为研究对象，分别简记为S1，S2，……，S10（如表1）.表1中的成绩指的是大一上学期的期中与期末的高等数学成绩平均分.

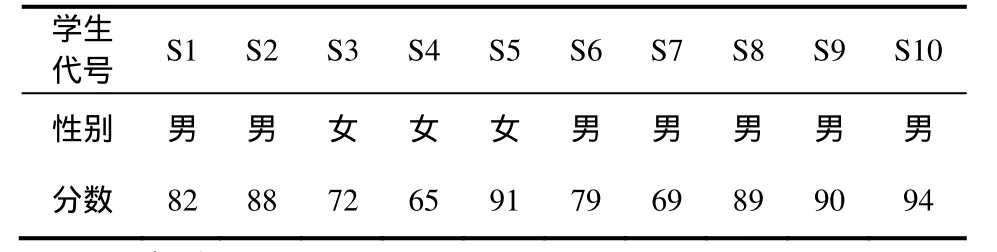
表1 学生情况简表

2.2 研究过程

采用质的研究方法，通过测试和访谈的途径来进行，主要包括5个问题，除微分外，还涉及到与微分有关的概念，如偏导数、切平面等.所有访谈均被录音并随后实录成文本以备分析.

3 研究结果

3.1 关于微分的计算

第1题：设函数z=esinx−2y，求dz.

10名同学都是按照公式dz=dx+dy来求dz.除了S9求得2esinx−2y而出错外，其余9位同学全部解对.

第2题：求球面x2+y2+z2=14在点（1, 2, 3）处的切平面方程.

10个同学全部通过求偏导数的方法，给出了正确的方程.

3.2 关于偏导数

第3题：什么是偏导数？

学生的回答见表2.

表2 大学生给出的偏导数概念

学生的答案中最多的实际上是偏导数的求法，如S9：“某一个函数有3个自变量x、y、z，如果对x求偏导的话，那么可以把y和z看作常量，然后对x求导数.”一些答案并不严格，如S1：“保持一个变量不变来求另一个变量对函数的导数.”但是，可以看出这些学生对偏导数的求法记忆深刻.

两位同学提到了符号化的定义.S8给出了非常准确的定义；S3给出了增量的比值形式，但是没有极限过程.S5指出“对立体作平行于xoy面或yoz面或xoz面的切面，偏导数即表示该切面与立体的交线的切线斜率”，并画出了示意图.只有S7提到了速率：“偏导数是（函数）沿x轴、y轴方向的增加速率.”S10提到：“当一个变量经过微小变化时，因变量的变化与自变量变化的商.”

3.3 关于全微分

第4题：请用尽可能多的方式给出全微分的定义，并解释你所给出的定义（如果你觉得有困难可以通过一元函数微分的几何意义来解释），答案见表3.

表3 大学生给出的全微分概念

尽管此题明确要求学生给出全微分的定义，但还是有学生用全微分的求法即dz=dx+dy来代替全微分的定 义，学生关注的更多的是如何求，而不是全微分的含义.事实上，只有在函数可微的前提下dz=dx+dy才表示z的全微分.

没有同学能够借助图形或用语言来描述二元函数全微分的几何意义，只有S2、S7、S10正确地指出一元函数微分的几何意义，并画出示意图；S5试图在点(x+Δx)画切线来表示函数f(x)在点x的微分；S3用f(x)在点x与(x+Δx)点的两条切线的增量差来表示微分.S9、S4想用教材中的y=x2增量的例子来说明微分的概念，但是他们不能指出究竟是哪一块面积代表的是函数的微分.S2没有给出全微分的定义.但是对于一元函数给出了一元微分的表达式dy=f'(x)dx，并画出了正确的示意图.S8没有给出全微分的定义，而是给出了一元函数的导数的定义，并将一元函数的导数和微分混淆.

第5题：请以概念图的形式尽可能多地写出与全微分有关的概念，并画出概念间的关系.

给出4个概念的有S2、S3、S6、S8、S9.S9给出了一元函数可导、可微、连续、极限存在之间的关系；S3在概念图旁用公式写出了一元、三元函数的微分求法、复合函数微分法则、二阶混合偏导数交换顺序的条件、二元函数极值点的判定规则，她记住了很多规则，而不是概念.S5给出了“极限、偏导、连续性、方向导数、梯度、偏微分、格林公式、高斯公式、与路径无关”；S1给出了“非线性问题的解决、不规则曲面的面积、微分中值定理、全增量、可微、可导、可偏导、复合函数求偏导法则”；S10的概念图最为丰富，共有15个概念，包括曲线的光滑性、凹凸性等.

4 关于学生概念认知类型的个案分析

Keith Weber[9]等人曾对学生的概念认知方式进行了研究，他们将学生的认知类型分为3类：

自然型：学生能对数学概念给予一个直观的描述，并且能由直观的描述导向形式化的思维，例如借助直观的描述来回忆、给出概念或进行证明.

形式化型：学生很少会直观想象他所使用的概念，也不会借助直观来推理，不过他能从逻辑的角度判断自己的证明是否正确.

程序型：学生通过记住解题程序来学习，当被问及为什么这样做时，他们无法给出准确的解释.

从研究结果来看，学生对概念的描述至少有4种，分别是几何意义、形式化的定义、解题程序和语言描述.因此，除了上述3种概念认知类型外，还有一种语义型.

语义型：学生不是借助直观图形，亦非记住形式化的定义，而是将形式化的定义转换为一种自然的语言来进行描述，从而将概念内化.

下文结合访谈情况对学生的认知类型进行分析.

（1）自然型：S5，S10.

S5喜欢借助图形来表示偏导数和微分的概念，在思考问题时她喜欢画一些几何图形.她说：“我不太懂抽象的关系.对概念一般都要先具象化，只有画出来才能想象.这可能与我的专业有关，因为机械制图都要画出来.”

S10对数学概念有比较深入和广泛的理解，在微分的概念图中他给出的概念最多，并能用语言准确地描述这些概念间的关系，能发现诸如“微分是泰勒公式的一阶形式”这样的关系.S10说他常常通过画图首先理解定义的几何意义，然后理解概念的形式化的定义.当理解、记住了形式化定义后，就不用借助画图来回想定义了.他喜欢在学习中思考概念间的联系.

（2）形式化型.

在本研究中，学生多借助于几何直观及运算程序来理解概念，而没有单纯依靠形式推理的情况，所以研究中没有发现形式化型的学生.

（3）程序型：S1、S3、S4、S8、S9.

研究中，通过“记住解题程序来学习”的学生最多，他们的共同点是记住了很多公式和结论，却并不一定理解.对S9的访谈共进行了70分钟.对于概念性的问题，他经常长时间地沉默思考.他更喜欢用解题方法来代替定义，而非定义本身.在访谈中，他反复要求研究者给他具体的题做，而不是回答概念，他说对于概念他只是“看一下”，主要看公式和例题.他认为画图的问题尤其是有关空间图形的问题比较难理解.

S8在回答全微分的定义时，他首先认为微分就是导数，接下来他描述微分过程时，又无法指出是对哪个量的微分；他记住了积分与微分关系的口诀，却无法理解二者是互逆的运算.以下为访谈片段，T表示访谈老师.

片段1：

（S8写了一元函数导数的定义来表示微分的定义.）

S8：导数和微分不一样？

T：你认为导数和微分是一样的？

S8：哦，差一点点.

T：差什么？

S8：我说的是导数，微分应该是导数乘以dx.

片段2：

T：全微分是怎样定义的，它有什么含义？

S8：这个不会.

而在《十日谈》中，薄伽丘正是在很多时候摆脱了这种二元对立[11]的简单结构，如第七天故事的主题为“妻子捉弄丈夫的故事”，而第八天的故事主题为“互相捉弄的故事”。这二十个故事足足占了整部作品五分之一的笔墨。仔细品味作家的语言，会发现薄伽丘笔下的那些捉弄丈夫的妻子，并非“魔鬼”，她们的结局也不都是悲惨的。相反，她们中有人凭借智慧得到了自己想要的东西，有人沉湎于婚外情中，却无法引起读者的愤恨，有人为自己的蠢笨付出代价，却只是为了博读者一笑。作品中，更多的女性像男性一样享受肉欲满足所带来的快感。可以说，薄伽丘并没有以一种胜利者的姿态对女性抱有同情的态度，在很多时候，他笔下的女性与男性并无差别。

T：全微分的几何意义是什么？如果你觉得很难解释的话，你可以用一元函数来说明.

S8：是不是就是把它分成n个，然后每个看成矩形，这个就是微分吧.（注：S8画了一个曲边梯形，然后分割，取了其中的一个小矩形.）

T：那这一块面积是对哪个函数的微分？

S8：是对曲线f(x)的微分.

（显然，S8回答错了，小矩形的面积应是面积函数F(x)的微分.）

片段3：

T：你认为在高等数学中引入全微分的概念有什么意义？

S8：引入全微分是积分的关键.

T：为什么？

S8：我现在还不明白积分和微分有什么不同.

T：没有学过吗？

S8：对，老师讲过，这两个有区别，一个有个常数，一个少了个常数.

T：先积后微和先微后积？

S8：对，先积后微形式不变，先微后积差个常数.我就知道这个.

T：那微分运算和积分运算是什么关系呢？

S8：不知道.

（4）语义型：S7.

S7喜欢用描述的语言接近概念的本质，对概念有大体的了解，但有时不够准确：“全微分是函数在定义域内各个方向上的微分之和”；“偏导数就是沿一个方向的导数，如沿x、y、z轴方向的方向导数”；偏导数就是“像速度一样的量”；“微分就是很小的变化量，导数就是变化速率”.数列的极限是“不管ε怎么小，都可以找出一个界点，在那个界点之后的数的差值都在那个范围之内”.

5 结论与建议

（1）学生对微分概念存在很多误解，建议加强概念尤其是核心概念的教学.

从研究结果来看，虽然9位同学都能计算具体函数的全微分，却只有两位同学能够给出全微分的形式化的定义；10位同学都能准确地计算出给定函数在一点的切平面，却没有同学能够通过图形或用语言来描述二元函数全微分的几何意义.一些同学知道微分的几何意义和切线有关，但是却不知究竟是哪条切线、切线上的哪个量表示微分，更不知用一次函数来近似代替f(x)的意义.在画微分概念图时，学生只能想出几个基本的概念却无法给出概念间的广泛的、准确的联系，一些同学只是像背口诀一样背出一元函数可导、可微、连续的关系，却无法解释为什么对于多元函数来说偏导数存在却不一定可微.建议在教学中，除了教授具体的计算方法之外，应加强概念，尤其是核心概念的教学，强调概念理解，从本质上揭示核心概念间的联系，这样才有助于学生形成关系性[10]概念理解的高质量图示，而非仅仅记住如“可导必连续”这样的命题，停留在工具性理解[10]的表面.研究表明[11]，对于数学专业和理工科的学生来说，在教学中加强概念理解，不仅不会削弱学生的解题能力，而且还会在加深学生对数学概念的认识的同时，提高其解题能力.

（2）学生具有多种概念认知模式，建议以多种表征进行概念教学.

从研究结果来看，学生具有多种概念认知模式，有的喜欢将形式化的定义用图像表示来帮助理解，有的喜欢用自然的语言而非数学的语言来描述.学生的认知类型，虽然不是一成不变的，会随着所学内容的不同而转化，但每个学生都会有一定的认知偏好.Ramond Duval[12]认为，从认知角度来看，一个表征不足以完成数学教学过程.在数学活动中，多种表征同时发挥作用，对数学的理解起源于不同类型表征的配合与协调过程，而数学教学的首要任务也是培养学生在不同表征间进行转化的能力.所以在微积分概念教学中，应注意加强概念的几何意义的教学，并多用自然的解释性的语言而非抽象的语言来阐述.这一点上，美国的一些做法值得借鉴.20世纪80年代末期兴起的微积分教学改革中提出了3原则，认为微积分的3个侧面：图像、数值和符号应贯穿始终，学生应在充分展现这3种形式的环境里体验微积分的概念[13].这些原则在一些美国教材[14]中得到了很好的体现.而目前我国的教学中还是比较注重形式化与程序化的知识，对概念的图像和数值的表征方式重视不够，这不利于学生的微积分学习.

（3）计算题难以对学生进行全面考核，建议改进考核方式.

本研究中，虽然不乏如S5、S10这样概念理解水平高、考试成绩也好的学生，但是也存在一些考试悖论：S8、S9的对微分概念存在误解，但是由于他们记住了一些具体的算法，考试成绩都在90分左右；S7的考试成绩为69分，他却能用自己的语言（虽然不是完全正确）阐述微积分概念的内涵.教学实践表明，凡是学生能用自己的语言复述概念的定义和解释概念所揭示的本质属性，那么他们对概念的理解就深刻[15]，也就能够记忆得更持久，更容易迁移.建议在高等数学考试中增加一些考查学生对概念理解的题目，这样可以提高学生学习概念的积极性，从而加深对数学的理解，形成高水平的关系型概念图示.

致谢：感谢浙江理工大学周远同学协助进行了繁琐的录音实录等工作！

[1]同济大学数学系.高等数学（第6版）[M].北京：高等教育出版社，2007.

[2]Kidron I.Abstraction and Consolidation of the Limit Procept by Means of Instrumented Schemes: The Complementary Role of Three Different Frameworks [J].Educational Studies in Mathematics, 2008, 69(3): 197−216.

[3]Barbé J, Bosch M, Espinoza L, et al.Didactic Restrictions on the Teacher’s Practice: The Case of Limits of Functions in Spanish High Schools [M].Beyond the Apparent Banality of the Mathematics Classroom, 2005.

[4]Bingolbali E, Monaghan J, Roper T.Engineering Students’ Conceptions of the Derivative and Some Implications for Their Mathematical Education [J].International Journal of Mathematical Education in Science and Technology, 2007,38(6), 763−777.

[5]Dubinsky E, Asiala M, Cottrill J, et al.The Development of Students Graphical Understanding of the Derivative [J].Journal of Mathematical Behavior, 1997, 16(4): 399−431.

[6]Baker B, Cooley L, Triguerous M.A Calculus Graphing Schema [J].Journal for Research in Mathematics Education,2000, 31(5), 557−578.

[7]朱卫平.大学一年级学生对微积分基本概念的理解[D].华东师范大学，2006.

[8]芦伟，陈浩.全微分概念的表征及教学对策[J].巢湖学院学报，2005，7（3）：50−51.

[9]Weber K.Traditional Instruction in Advanced Mathematics Courses: A Case Study of One Professor’s Lectures and Proofs in an Introductory Real Analysis Course [J].Journal of Mathematical Behavior, 2004, 23(2): 115−133.

[10]Skemp, Richard R.Relational Understanding and Instrumental Understanding [J].Mathematics Teaching, 1977, (1):20−26.

[11]Chappell K K.Effects of Concept-Based Instruction on Calculus Students’ Acquisition of Conceptual Understanding and Procedural Skill [A].In: Hitt F, Harel G, Selden A.Research in Collegiate Mathematics Education VI [C].Washington,D C: American Mathematical Society, 2006.

[12]Duval R.A Cognitive Analysis of Problems of Comprehension in a Learning of Mathematics [J].Educational Studies in Mathematics, 2006, 61(1), 103−131.

[13]王高峡，唐瑞芬.再谈美国的微积分教学改革[J].数学教育学报，2000，9（4）：54.

[14]芬尼，韦尔，焦尔当诺.托马斯微积分[M].叶其孝，王耀东，唐兢译.北京：高等教育出版社，2003.

[15]鲍建生.数学语言的教学[J].数学通报，1992，31（10）：1−2.