Fe-X（Mn，Si）合金稳定性和弹性性能的第一性原理研究

户秀萍，张彩丽，王小宏，张齐娜，董 楠，韩培德

（太原理工大学 材料科学与工程学院，新材料界面科学与工程教育部重点实验室，太原 030024）

钢的合金化是改善其组织结构和力学性能的主要方式之一，添加适量的合金化元素可提高钢铁材料的力学性能和工艺性能。钢中常加的合金化元素有C、Cr、Mn、Mo、W、Ni、Si、Ti、Nb、V等，这些合金化元素主要以固溶强化、第二相强化，以及细晶强化等方式发挥其作用[1-2]。Fe-Mn-Si系合金是常用的一类低合金钢，如65Mn、60Si2Mn等，常被用于抗疲劳性、弹性极限要求高的场合。宏观来看，Mn能提高钢的淬透性和强度，Si能提高钢的弹性极限、屈服强度和疲劳极限[3-4]。如 Miyamoto[5]等用扫描电子显微镜、透射电子显微镜等分析了Mn和Si对Fe-C（C的质量分数为0.6%）中第二相渗碳体形成过程的影响，发现Mn、Si的加入在降低渗碳体的形成速率的同时，可使基体相bcc-Fe更加稳定。Bliznuk[6]等实验研究了Fe-Mn-（Si、Cr、Ni、C和 N）合金中各元素的作用，得出Si、Ni的固溶有利于提高合金化元素在bcc-Fe中的均匀性。Uenishi[7]等研究了IF钢中合金化元素Mn和Si的固溶特性，Mn和Si的固溶有利于钢在高、低应变速率下强韧性的调配。尽管Si、Mn等合金化元素的作用机制已进行了大量的实验研究，但其原子层次的微观作用机制尚不完全清楚。

近年来，随着计算材料科学的发展，从原子尺度研究合金化元素在合金中作用机制，以及预测新的合金化成分体系已经成为研究的热点。Gebhardt[8]等用第一性原理的方法计算了面心立方结构Fe-Mn-Si合金的弹性模量，得出Si含量对弹性性能有不同程度的影响，当Si的原子数分数大于8%时，剪切模量和杨氏模量将分别降低7%和6%；Ohnuma[9]等计算了Mn、Si、Ti、Cr等合金元素在体心立方结构Fe中占位及结构稳定性的影响。Zhang Hualei[10]等比较了体心立方的 Fe1-x（M＝Al、Si、V、Cr、Mn、Co、Ni和Rh）的结构和力学性能。Mn、Si作为重要的合金化元素，其原子层次对力学性能的影响机制，尤其是Mn、Si合金化元素复合固溶于α-Fe所产生的协调作用机理，目前尚缺乏原子层次上的系统认识，因此从微观的原子水平探索Mn、Si固溶于体心立方Fe的结构稳定性和弹性性能是非常有必要的。笔者将利用第一性原理平面波超软赝势方法，对Mn、Si固溶于体心立方Fe的结构稳定性、电子结构及其弹性性能进行研究，并从电荷密度和态密度进一步解释其对α-Fe-Mn-Si合金的微观作用机理。

1 理论模型与计算方法

1.1 理论模型

本文以α-Fe为研究对象，空间群为Im-3m，晶格常数为a＝b＝c＝0.2866nm，α＝β＝γ＝90°。在计算中采用2×2×2的超晶胞作为完整晶体的计算单元，总原子数为16个，组成为Fe16，用 Mn、Si原子分别替代Fe作为Mn和Si固溶于α-Fe晶体形成的Fe-Mn、Fe-Si固溶体，对应的超晶胞为Fe15Mn和Fe15Si；用Mn、Si原子同时替代Fe形成的α-Fe-Mn-Si固溶体（Fe14MnSi）。α-Fe超晶胞以及Fe15 Mn、Fe15Si和Fe14MnSi结构模型见图1所示。

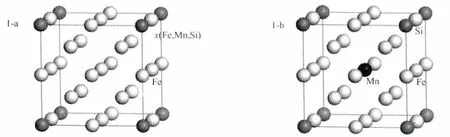
图1 固溶后的超晶胞结构模型

1.2 计算方法

采用基于第一性原理的密度泛函理论（Density Functional Theory），结合平面波赝势方法的Castep软件包对α-Fe-X（X＝Fe，Mn，Si）合金体系进行研究。计算中，采用周期性边界条件，性能计算用广义梯度近似 （GGA）中的PBE来处理电子间的交互关联能，Fe、Mn、Si各原子的价电子组态分别为Fe：3d64s2，Mn：3d54s2，Si：3s23p2；平面波的截断能为330eV，第一布里渊区k矢量的选取为10×10×10。结构优化的收敛条件为每个原子的能量变化在2.0×10-5eV以内；原子最大受力不超过0.5eV／nm；最大压力不超过0.1GPa；最大位移不超过0.0002nm。优化后的超晶胞结构再进一步计算电子结构、弹性性能等。

2 结果与讨论

首先采用选定的参数对α-Fe单胞进行结构优化并计算其性能，优化后α-Fe单胞参数为0.2856 nm，与实验值0.2866nm[11]很接近。计算得到的单晶弹性常数 C11、C12和 C44值分别为 259.53，134.47，119.53GPa，与相应的实验值245，139，122 GPa[11]相比误差很小，分别为5.85%，3.26% 和2.02%，说明本文选取的计算方法是可信的。

2.1 结构稳定性

晶体的结构稳定性与其结合能密切相关。晶体的结合能是自由原子结合为晶体所释放的能量，即晶体分解成单个原子时外界所做的功。结合能的绝对值越大，则形成的晶体越稳定[12]，结合能计算公式[13]为：

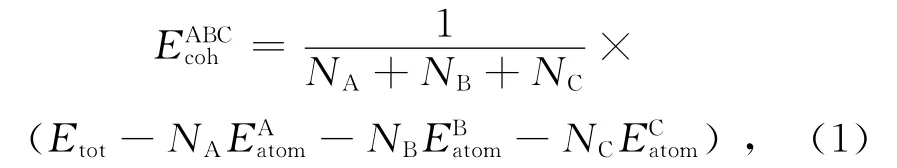
形成热用来考察合金系形成的难易程度，也常用来说明金属间化合物以及固溶体的合金化能力。形成热的绝对值越大，表示合金化的能力越强。为了分析合金元素的合金化能力，下面对合金体系的形成热进行计算，形成热的计算公式为[14]：

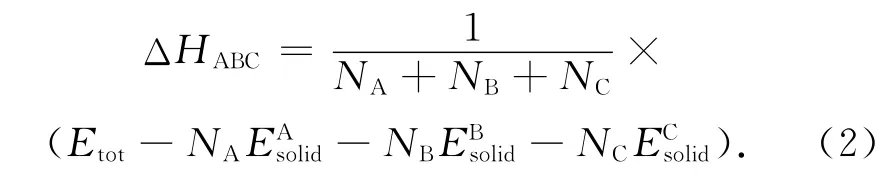
式中：ΔHABC为形成热；Etot为超晶胞的总能量，分别为单质Fe、Mn和Si平均每个原子的能量；NA，NB和NC分别为单胞中Fe、Mn和Si的数量。表1给出了α-Fe-Mn-Si合金体系的形成热，可以看出各合金形成能力由强到弱顺序为Fe14MnSi，Fe15Mn，Fe15Si。总体来看，Si、Mn复合合金化体系Fe14MnSi最易形成。

表1 α-Fe-X（Mn、Si）合金的单胞参数a，体积V，结合能Ecoh和形成热ΔH

2.2 弹性性质

2.2.1 单晶的弹性性质

不同晶系中独立的弹性常数个数不同，立方晶系中有3个独立的弹性常数，分别为C11、C12和C44。各合金弹性常数Cij（i＝1～6，j＝1～6）大小如图2所示。从图2数值来看，均满足（C11-C12）＞0，C11＞0、C44＞0，（C11＋2C12）＞0[15]的条件，说明各合金体系满足力学稳定性条件，可以稳定存在。

由图2可以看出，Mn、Si单独和复合固溶于Fe晶体后，对C11、C12和C44数值的影响是不同的。固溶均使C11降低，Fe15Mn、Fe15Si和Fe14MnSi分别为 由 α-Fe 的 259.33GPa 减 小 了 3.45，13.11，29.24GPa，C11的降低说明合金化体系在[100]方向抗变形能力减弱。具体来看，Mn、Si复合固溶的影响较单独固溶影响更为明显，Mn、Si均使C12数值增大，分别增加20.44，4.39GPa；但 Mn、Si复合固溶后却使C12数值减小11.69GPa；C44值都有所增大，Fe15Mn、Fe15Si和Fe14MnSi增加值分别为9.30，7.52，10.07GPa；C12、C44分别反映的是合金体系在[111]、[011]方向的抗变形能力，可以看出除复合固溶使体系在[111]方向抗变形能力明显降低外，其他情况均使抗变形能力增加。立方晶系单晶的剪切模量用C′＝（C11-C12）／2来表征，由图2-d可以看到，合金化后的C′都降低了，其中Fe15Mn的剪切模量C′最小，为50.29GPa；其次为Fe14MnSi，C′值为51.46GPa；Fe15Si的C′值为53.68GPa。Fe15Mn各弹性常数均比Fe15Si大，说明Mn对抗变形能力的影响大于Si。

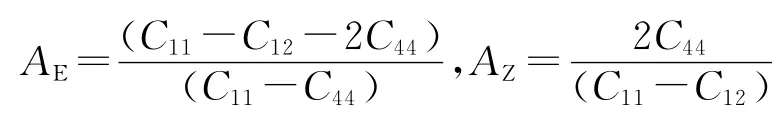
2.2.2 多晶的弹性性质

图2 合金的弹性常数

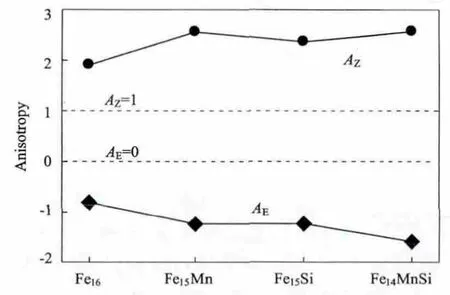
图3 合金的弹性各向异性

材料的力学性质在宏观上体现为材料的延展性、脆性、硬度、强度等方面。与之相对应，在微观上，通过一系列的物理量如弹性常数、体模量、杨氏模量、剪切模量、泊松比、体模量／剪切模量的比值等来体现。

多晶的弹性模量可由单晶的弹性常数进一步计算得到，笔者将采用VRH[18-20]的计算方法。体模量BH、剪切模量GH和杨氏模量E的计算如下：

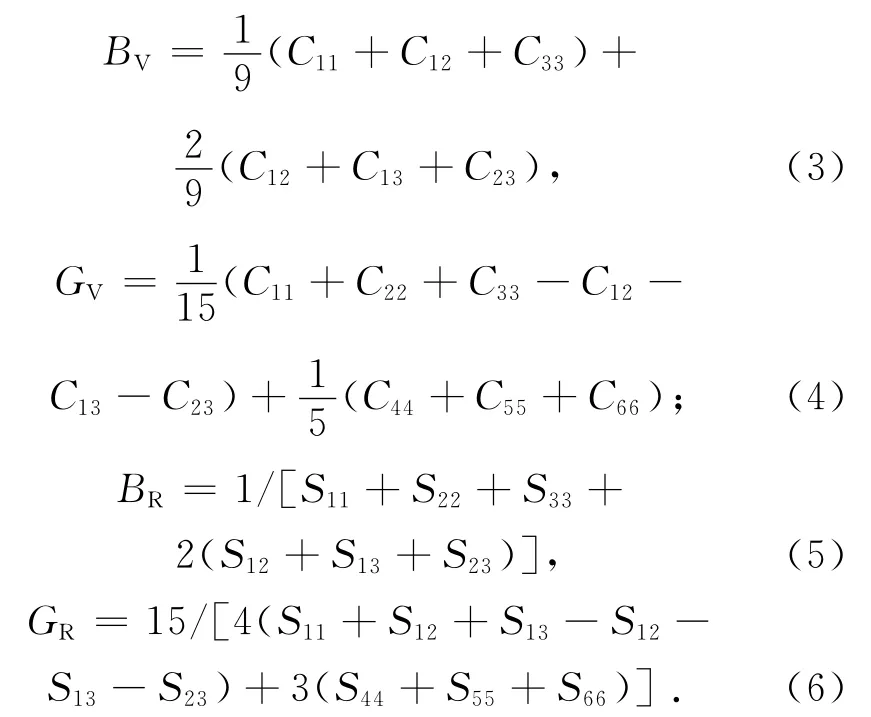
由此，可得出：

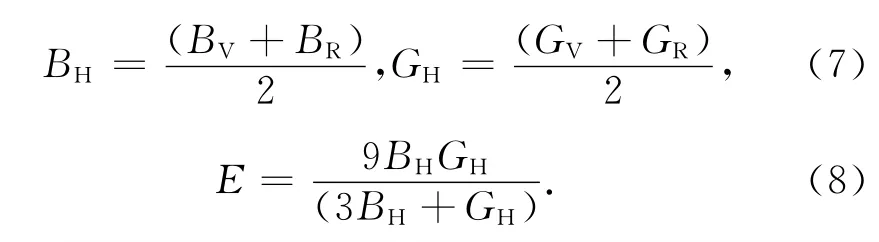
依据以上公式，合金Fe16、Fe15Mn、Fe15Si和Fe14 MnSi各弹性常数见图4所示。

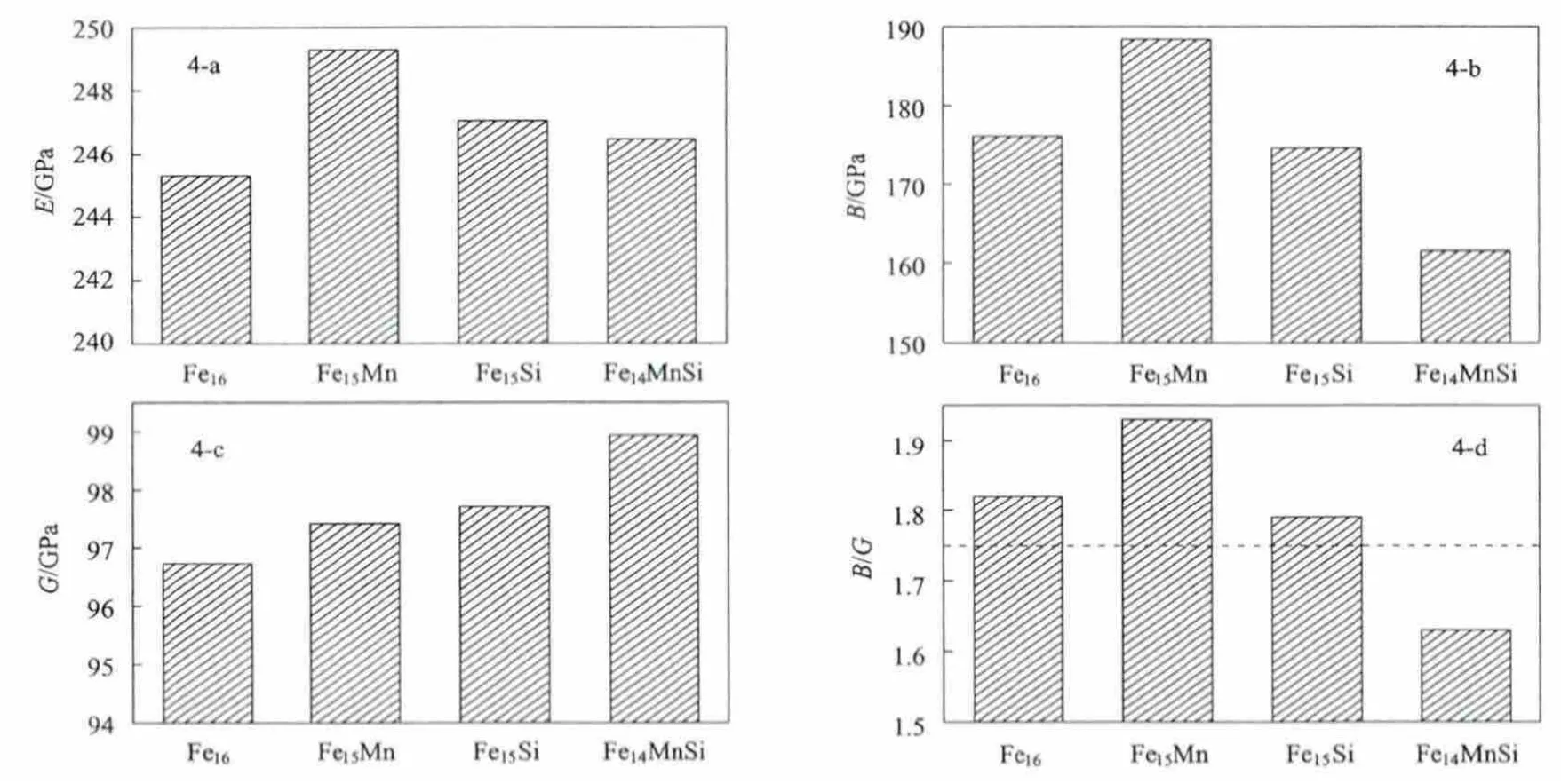
图4 合金的弹性性能比较

通常材料的刚度随杨氏模量E的增大而增强，材料的强度也与切变模量G和杨氏模量E密切相关，虽然不同晶系材料的强度与弹性模量的关系略有差别，但一般G和E的值越大，则材料的强度越高、硬度越大、耐磨性也越好[21]。由图4可以看出，Mn、Si单独和复合固溶于Fe晶体后，均使杨氏模量E有一定程度提高，增大的幅度分别为1.63%、0.71%和0.49%，可以看出复合溶入后对体系的影响反而减弱。对体模量B来讲，Mn单独固溶使B增大6.97%，而Si使B 减小0.68%，Mn、Si复合固溶使体模量B减小达8.33%。Mn、Si单独和复合固溶α-Fe后合金的剪切模量G有少量提高，分别增大0.70%、1.00%和2.28%。由B／G 的值可以看出各合金延展性的差异，Fe15Mn的延展性最好，而Fe14MnSi的延展性相对较差，各合金延展性由强到弱顺序为：Fe15Mn＞Fe15Si＞Fe16＞Fe14MnSi，即Mn、Si单独固溶可提高合金体系的韧性，而复合固溶使体系的脆性增大。

2.3 电子特性

为探索Mn、Si元素掺杂α-Fe对结构稳定性、力学性能影响的微观机制，我们对Fe15Mn，Fe15Si和Fe14MnSi的总态密度和分波态密度进行了分析，如图5所示。

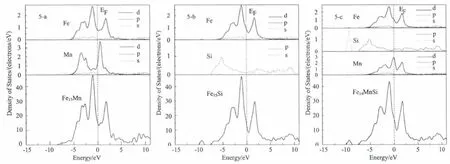
图5 合金的总态密度和分波态密度

Fe15Mn的成键电子主要分布在-8～11eV区间，主要由Fe-3d、Mn-3d的价电子贡献；-1.2eV附近的价带区由Fe-3d轨道贡献；费米面附近的价带来源于Fe-3d轨道和Mn-3d轨道的共同作用。Fe15Si的成键电子主要分布在-10～11eV区间，主要由Fe-3d、Si-3p、Si-3s的价电子贡献；-1eV 附近的价带区由Fe-3d轨道贡献；-9.5eV附近的价带区由Si-3s轨道贡献；费米面附近的价带主要来源于Fe-3d轨道贡献。Fe14MnSi的成键电子主要分布在-10～11eV区间，主要由Fe-3d、Si-3p、Si-3s、Mn-3d的价电子贡献；-1.1eV附近的价带区由Fe-3d轨道贡献；-9.5eV附近的价带区由Si-3s轨道贡献；费米面附近的价带主要来源于Fe-3d轨道和Mn-3d轨道共同作用。因此，我们得出Fe15Mn、Fe15Si和Fe14MnSi费米能级下的电子数分别为120.56，123.58，122.45。在费米能级下，较低等级形成新的成键峰及费米能级以下较多的价电子是结构稳定性和结合能增强的原因，Si的加入使合金在费米能级下较低的等级形成了新的成键峰，从而使合金成键峰增多，结合能增强，这与之前所研究的合金稳定性相符。

差分电荷密度图对原子间的成键及电荷得失可给出一个直观的图像。为了更直观地分析合金元素Mn、Si合金化后对α-Fe电荷分布的影响，图6显示出了Fe16、Fe15Mn、Fe15Si和Fe14MnSi（011）面的差分电荷密度图。从图6可以看出，与α-Fe相比较，合金化后体系的电荷发生了重新分布，Fe-Mn体系中，Mn原子得到电子，邻近的Fe原子失去电子，Mn与邻近Fe原子间的电荷密度增大，使Fe、Mn相互作用增强；Fe-Si体系中，Si失去电子，邻近Fe原子得到电子，Fe原子间电荷密度增大，Fe-Fe相互作用增强；Mn、Si复合固溶的Fe-Mn-Si体系中，Mn和Si原子都失去电子，与邻近Fe原子间电荷密度增大，Fe-Mn和Fe-Fe相互作用都增强了。

图6 合金的差分电荷密度分布

3 结论

基于密度泛函理论的第一性原理平面波赝势方法，计算了Fe-Mn、Fe-Si和Fe-Mn-Si合金体系的稳定性及弹性性能。计算发现，Fe-Mn、Fe-Si和Fe-Mn-Si均满足热力学和力学稳定性条件，且热力学稳定性由强到弱顺序为Fe15Si、Fe16、Fe14MnSi、Fe15Mn。对于单晶体系，Mn、Si单独和复合固溶于bcc-Fe晶体后，均使C11降低，复合合金化影响程度大于单一元素的影响，固溶后合金体系在[100]方向抗变形能力减弱。Mn、Si均使合金体系C12、C44数值增大，而 Mn、Si复合固溶后却使C12数值减小、C44值增大，即除复合固溶使体系在[111]方向抗变形能力明显降低外，均使抗变形能力增加。对于多晶体系，Mn、Si单独和复合固溶于Fe晶体后，均使杨氏模量E有一定程度提高；Mn单独固溶使体模量B增大，而Mn、Si复合固溶使体模量B大幅度减小。总体来看，Mn、Si单独固溶可提高合金体系的韧性，而复合固溶使体系的强度增大，合金延展性由强到弱顺序为：Fe15Mn、Fe15Si、Fe16、Fe14MnSi。

[1]吴成建，陈国良，强文江.金属材料学[M].北京：冶金工业出版社，2009：3-5.

[2]Khvan A V，Hallstedt B.Thermodynamic description of the Fe-Mn-Nb-C system[J].Calphad，2012，39：62-69.

[3]Zhang C L，Liu Y Z，Jiang C，et al.Effect of niobium and vanadium on hydrogen-induced delayed fracture in high strength spring steel[J].Journal of Iron and Steel Research，2011，18（6）：49-53.

[4]刘兵，何国求，蒋小松，等.60Si2Mn钢的低周拉扭复合微动疲劳特性[J].材料研究学报，2010，24（1）：61-68.

[5]Miyamoto G，Oh J C，Hono K，et al.Effect of partitioning of Mn and Si on the growth kinetics of cementite in tempered Fe-0.6mass%C martensite[J].Atca Mater，2007，55：5027-5038.

[6]Bliznuk V V，Gavriljuk V G，Kopitsa G P，et al.Fluctuations of chemical composition of austenite and their consequence on shape memory effect in Fe-Mn-（Si，Cr，Ni，C，N）[J].Acta Mater，2004，52：4791-4799.

[7]Uenishi A，Teodosiu C.Solid solution softening at high strain rates in Si-and／or Mn-added interstitial free steels[J].Atca Mater，2003，51：4437-4446.

[8]Gebhardt T，Music D，Kossmann D，et al.Elastic properties of fcc Fe-Mn-X（X＝Al，Si）alloys studied by theory and experiment[J].Acta Mater，2011，59：3145-3155.

[9]Ohnuma T，Soneda N，Iwasawa M.First-pinciple calculations of vacancy-solute element interactions in body-centered cubic iron[J].Atca Mater，2009，57：5947-5955.

[10]Zhang H L，Punkkinen M P J，Johansson B，et al.Single-crystal elastic constants of ferromagnetic bcc Fe-based random alloys from first-principles theory[J].Phys Rev B，2010，81：184105.1-184105.14.

[11]Clatterbuck D M，Chrzan D C，Morris J W.The ideal strength of iron in tension and shear[J].Acta Mater，2003，51（8）：2271-2283.

[12]张彩丽，李晋敏，韩培德，等.Cr对Ni3Al合金化效应的赝势平面波方法[J].稀有金属材料与工程，2008，37（10）：1705-1709.

[13]Sahu B R.Electronic structure and bonding of ultralight LiMg[J]Mater Sci Eng B，1997，49（1）：74-78.

[14]Wu M M，Wen L，Tang B Y，et al.First-principle study of elastic and electronic properties of MgZn2and ScZn2phases in Mg-Sc-Zn alloy[J].J Alloys Compd，2010，506：412-417.

[15]Li L，Yu W，Jin C.First-principle calculations of a high-pressure synthesized compound PtC[J].Physics Condensed Matter，2005，17（38）：5965-5970.

[16]Every A G.General closed-form expressions for acoustic waves in elastically anisotropic solids[J].Phys Rev B，1980，22（4）：1746-1760.

[17]Zener C.Elastisity and Anelasticity of Metals[M].Chicago，University of Chicago Press，1948：69-79.

[18]Voigt W.Lehrbuch der Kristallphysik[M].Teubner，Leipzig，1928：962-963.

[19]Reuss A.Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals[J].Angew Math Mech，1929，9：49-58.

[20]Hill R.The elastic behavior of a crystalline aggregate[J].Proc Phys Soc A，1952，65：349-354.

[21]曾宪波，彭平.α2-Ti-25Al-xNb合金力学性质的第一原理计算[J].金属学报，2009，45（9）：1049-1056.