基于EMD-HT的齿轮箱故障特征提取技术研究

曹凤才，潘宏侠

（中北大学 计算机与控制工程学院，太原 030051）

故障特征提取是故障诊断领域的关键技术之一，即从所检测到的状态振动信号中提取故障征兆。直接由测试信号来判断设备的运行状态是比较困难的，因此需要对测试信号进行分类、加工，变换以提取故障特征，在智能故障诊断中要求提取数字特征[1]。

Hilbert-Huang变换（HHT）是近年来发展起来的一种信号自适应时频分析方法，该方法最早是由美国国家宇航局的Norden E.Huang提出的。本文参照HHT能量谱分析的齿轮箱故障诊断流程，提出了基于EMD-HT的瞬时能量分布和Hilbert边际谱特征提取方法，如图1所示，并进行了实验验证。从而实现对复合故障在内的齿轮箱多种典型故障的有效诊断[2-3]。

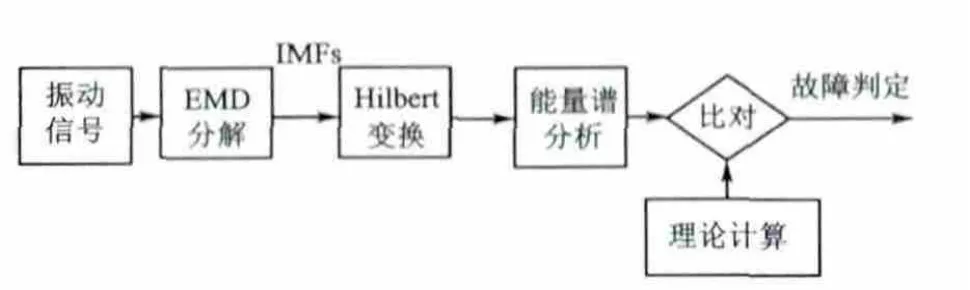
图1 基于HHT能量谱分析的齿轮箱故障诊断方法框图

1 Hilbert-Huang变换的基本原理[2-6]

1.1 Hilbert变换

给定一个连续的时间信号x（t），可以得到它的Hilbert变换y（t）为：

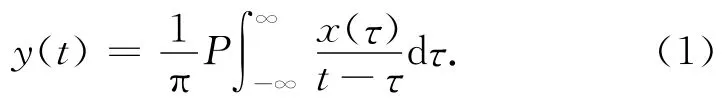
式中，P为柯西主值。这一变换对所有x（t）和y（t）可形成一个共轭对z（t）：

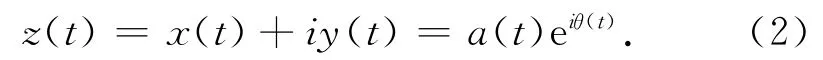
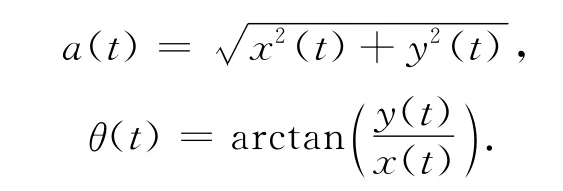
瞬时频率定义为下式：

1.2 本征模态函数

IMF是满足单分量信号物理解释的一类信号。和简单的单调函数相比，一个内在模态函数代表了一个简单的振动模态。一个本征模式函数应该符合下面两个条件[7，9]：在整个数据段内，极值点的数目与过零点的数目必须相等或者至多相差一个；在任意时刻，由局部极大值点相连构成的上包络线与由局部极小值点相连构成的下包络线的平均值为零。即上、下两包络线关于时间轴局部对称。

1.3 EMD方法

本征模态函数经过Hilbert变换得到的瞬时频率有意义。但是，几乎所有要分析的信号数据都不是本征模态函数，在任意时间点上，信号数据可能包含多个波动模式，这就是由Long等人所报道的简单Hilbert变换不能完全表征一般信号数据频率特性的原因。为了能把一般信号数据分解成本征模态函数，Norden E.Huang等人提出了 EMD方法[3，7，9]。EMD分解方法利用局部极大值和极小值的包络来进行。一旦获得所有极值点，所有的局部极大值用三次样条插值函数插值形成数据的上包络线，同样，所有的局部极小值通过插值形成数据的下包络线，上包络和下包络的平均值记作m1，原数据x（t）减去m1得到h1：

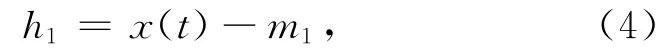
把h1作为原信号，重复上面的步骤，得到：

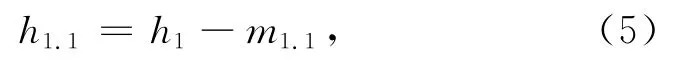
反复筛选k次，直到h1.k变为IMF，即：

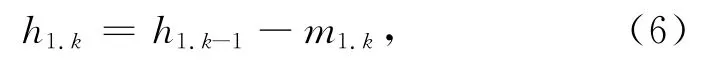
记c1＝h1.k，则c1为信号x（t）第1个满足本征模态函数条件的分量。

因剩余部分r1仍旧包含着较长周期的成分，因此可以继续利用上面介绍的筛分过程对r1进行分解，从而获得第2阶内在模态函数分量，重复这个过程可以得有一定数目的内在模态函数分量：

5)GB/T 20258.4—2007《基础地理信息要素数据字典 第4部分：1∶250 000 1∶500 000 1∶1 000 000基础地理信息要素数据字典》。

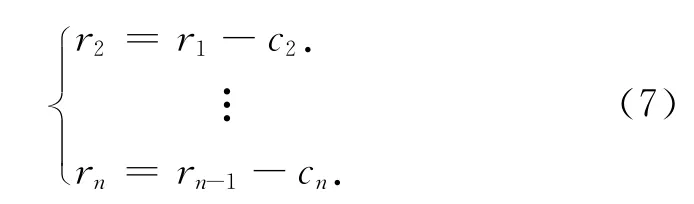
最终获得信号表示为本征模态函数分量和余量rn的表达式：

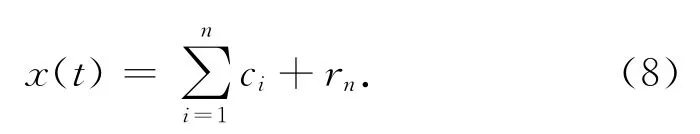
1.4 Hilbert谱和边际谱

对所有已分解出的IMF作Hilbert变换，忽略残余分量rn，在T-f平面上的幅值分布图即Hilbert幅值谱，简称Hilbert谱。记为：

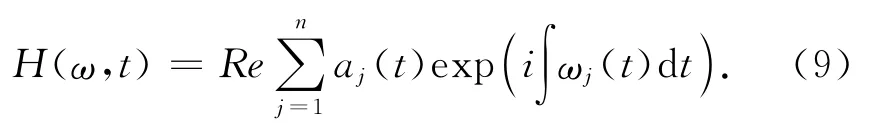
H（ω，t）反映了信号的幅值、时间和瞬时频率之间的关系。

定义Hilbert边际谱为：

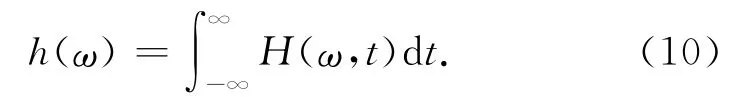
h（ω）反映了信号的幅值和瞬时频率之间的关系。可以进一步定义Hilbert（边际）能量谱为：E（ω）精确描述了信号能量随瞬时频率的规律分布情况[10-12]。

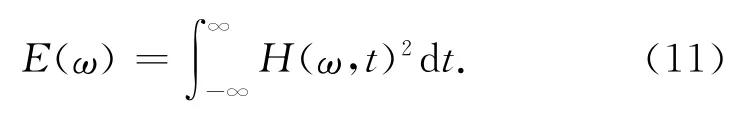
2 齿轮故障诊断实例[7-10]

2.1 实验装置

实验以JZQ250型齿轮箱为研究对象，滚动体直径d＝19.05mm，节圆直径D＝60mm，滚子个数为6个。齿轮箱传动和测点布置示意图如图2所示，实验系统由Y132S-4三相异步电动机驱动，电机输出轴经由连轴器与齿轮箱的输入轴相连，再由齿轮箱传动，传递动力于负载轮，最后经由抱紧装置抱住。

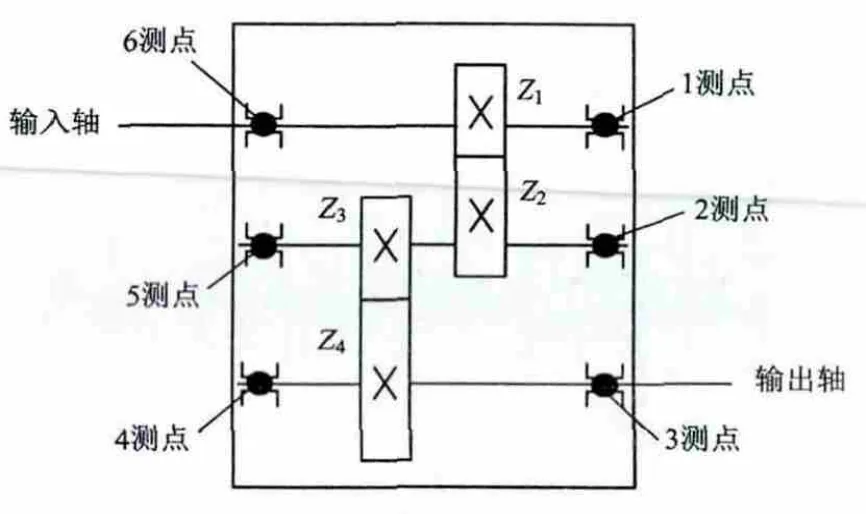
图2 齿轮箱传动和测点布置示意图

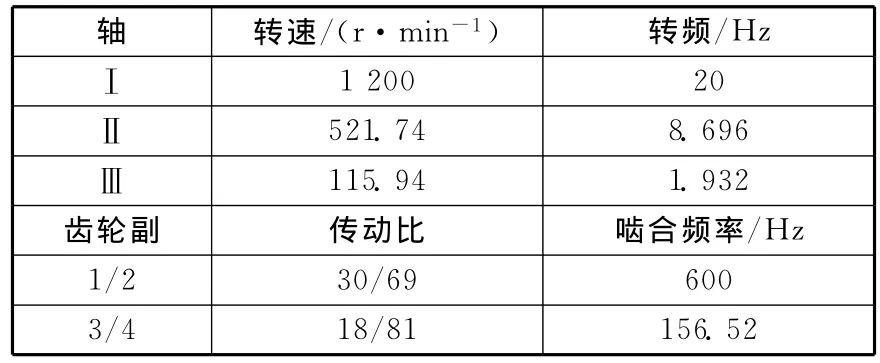
表1 齿轮箱各轴转频及啮合频率

表2 中间轴轴承的特征频率（Hz）

2.2 故障设置

依据工程经验，JZQ250型齿轮箱在实际使用过程中，中间轴容易出现故障，包括轴承疲劳剥落，保持架损坏以及齿轮断齿等。本次试验选取齿轮轻载时的故障数据，模拟中间轴轴承保持架发生单一故障和中间轴轴承外环加保持架复合故障。在箱体轴承座上方处安装了6只压电式加速度传感器试验主要测取了三相异步电动机转速为1200r·min-1时，输入轴、中间轴和输出轴两侧Ⅰ-Ⅵ测点的振动加速度信号，并对这6个测点测得的振动加速度信号进行分析计算。试验采样频率设置为20000 Hz，同时对信号进行重采样，重采样频率设置为4000Hz。实验预先对信号进行低通滤波，防止重采样造成频率混叠。

2.3 试验数据分析

2.3.1 保持架故障数据分析

设置中间轴Ⅱ处轴承保持架发生故障时的时域波形如图3所示。分析该时域波形图，可以看出故障信号波形中存在着分布较密集近似周期性的脉冲，表明该部位存在故障，但还不能精确确定故障部位与类型。该故障信号的经验模式分解（EMD）方法分解结果如图4所示，得到的本征模函数分量依然呈现某种周期性特征，说明存在故障，仅观察该图无法实现诊断。接下来通过对本征模函数分量组进行Hilbert变换可以得到Hilbert边际谱如图5所示。

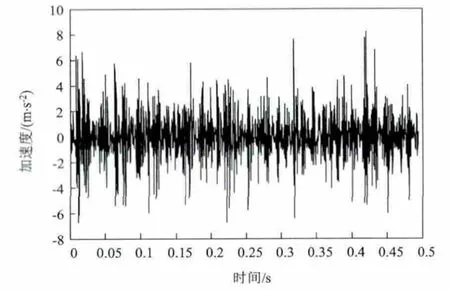
图3 保持架故障时域波形

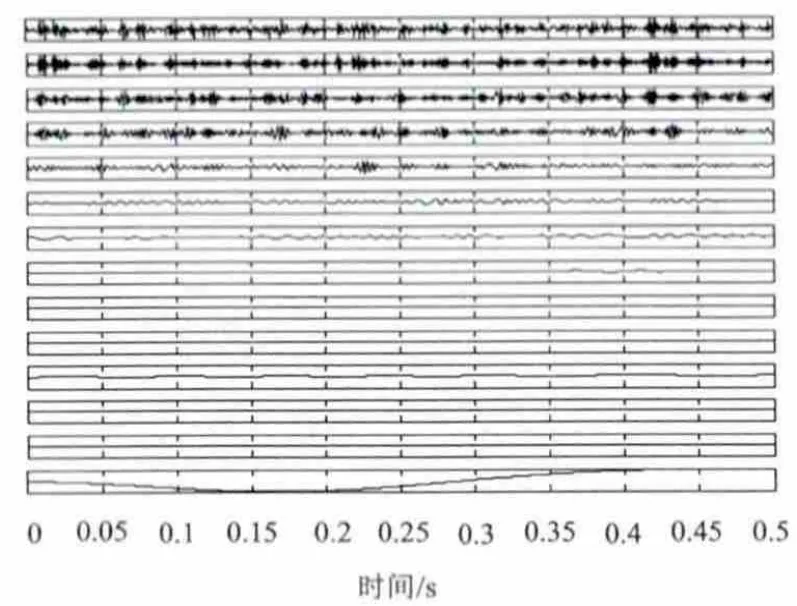
图4 保持架故障信号的EMD分解结果

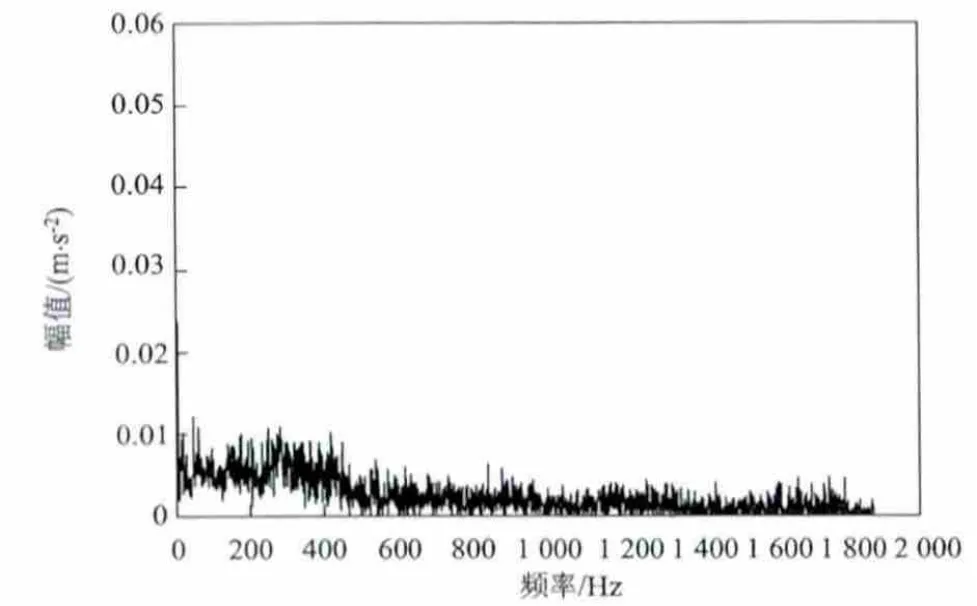
图5 保持架故障信号的边际谱

从Hilbert边际谱可以得到能量主要集中在0～500Hz频段内。观察到在图6中只存在一条明显的特征谱线，频率为3.41Hz的特征谱线与中间轴轴承保持架的特征频率fb＝3.37Hz基本吻合。从而可以判断中间轴的轴承保持架发生了故障。

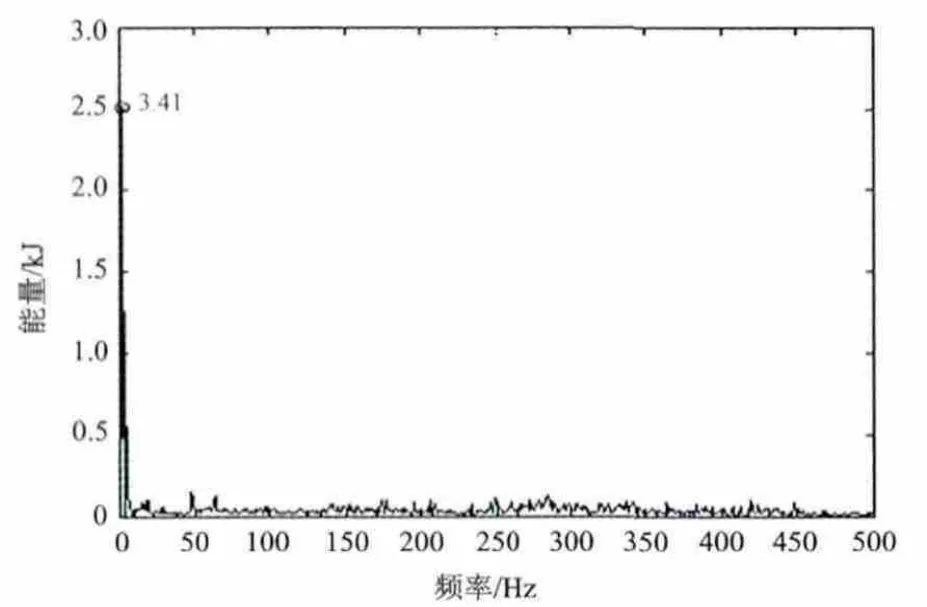
图6 保持架故障信号的局部能量谱

2.3.2 轴承外环加保持架复合故障数据分析

设置中间轴Ⅱ处轴承外环与保持架同时发生故障时的振动信号的时域波形如图7所示。分析该时域波形图，可以看出故障信号波形中存在着分布较密集近似周期性的脉冲，与轴承故障波形相似，但还不能精确确定故障部位与类型。将该故障信号按经验模式分解（EMD）方法分解结果如图8所示。仅从EMD分解结果图无法直观得出出该信号中所包含故障特征。接下来通过对本征模函数分量组进行Hilbert变换可以得到Hilbert边际谱，如图9所示。

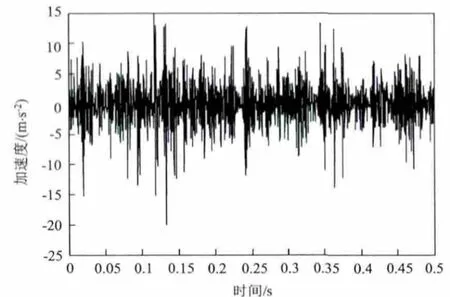
图7 轴承外环加保持架复合故障时域波形

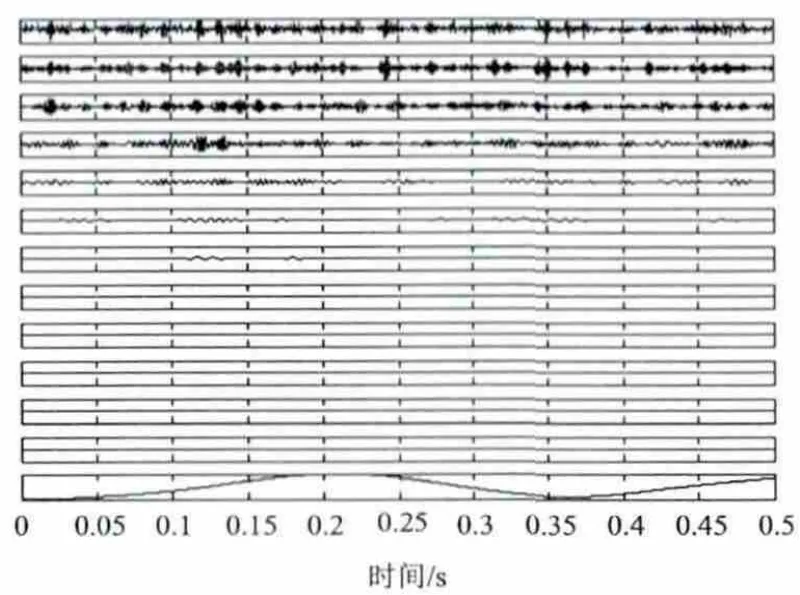
图8 轴承外环加保持架复合故障的EMD分解

图9 轴承外环加保持架复合故障信号边际谱

从Hilbert边际谱可以得到，在0Hz附近有谱线明显高于其他谱线，该谱线大致发生在270Hz左右，270Hz以前的频段谱线幅值呈上升趋势；而270 Hz以后的频段的谱线幅值呈下降趋势。该谱图中小于500Hz的频段集中了高幅值部分。

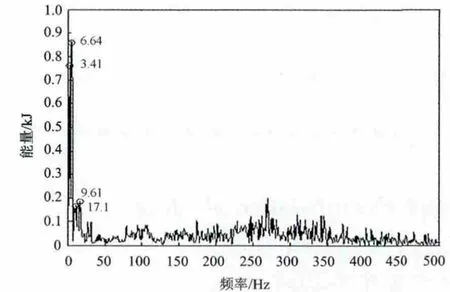
图10 轴承外环加保持架复合故障信号的能量谱

图10为对500Hz以内频段进行能量分析后，得到的（局部）能量谱谱图。在（局部）能量谱谱图中，可以观察到在3.41，6.64，9.61，17.1Hz等处存在明显谱线。其中，17.1Hz与中间轴轴承外环特征频率fout＝17.8Hz基本对应，而9.61Hz与中间轴旋转频率f2r＝8.696Hz大致对应，而3.41Hz，6.64Hz与轴承保持架的特征频率fb＝3.37Hz及轴承保持架特征频率的2倍频吻合，从而可以判断中间轴的轴承外环和保持架同时发生了故障。

3 结论

提出了基于EMD-HT的瞬时能量分布故障特征提取方法，从齿轮传动系统发生异常与其瞬时能量分布变化之间的理论关系研究入手，通过人为设置单个元件单一故障和多个元件复合故障，通过实验采集到的齿轮箱故障振动信号进行分析，并将该故障信号按经验模式分解（EMD）方法分解后得到本征模函数分量组，通过对本征模函数分量组进行Hilbert变换可以得到Hilbert边际谱，在0～500 Hz以内频段进行能量分析后，得到能够精确反映信号频率随其能量变化的规律的（局部）Hilbert能量谱，在此基础上提出了基于EMD-HT的瞬时能量分布和Hilbert边际谱特征提取方法，并进行了实验验证。

实验验证结果表明：当齿轮箱发生单一故障或者复合故障时，各故障元件的特征频率谱线依然能够在（局部）Hilbert能量谱谱图中体现出来。基于EMD-HT算法能够获得齿轮箱故障信号的频率特征，从而能够有效的识别齿轮箱故障类型。

[1]Long S R，Huang N E.On the Normalized Hilbert Transform and Its Applications in Remote Sensing.Signal And Image Processing for Remote Sensing[M].New York：CRC Press New York，2006：3-22.

[2]Yu Dejie，Cheng Junsheng，Yang Yu.Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings[J].Mechanical Systems and Signal Processing，2005，19（2）：259-270.

[3]Liu B，Riemenschneider S，Xu Y.Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum[J].Mechanical Systems and Signal Processing，2006（20）：718-734.

[4]郝云虎.小波变换在齿轮箱故障诊断中的应用[D].太原：中北大学硕士学位论文，2009.

[5]Huang N E，Shen Z，Long S R.The Empirical Mode Composition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J].Proc R Soc London，1998，454：903-995.

[6]Li Hui，Zhang Lichen，Zheng Haiqi.The application of Hilbert-Huang transform energy spectrum in bearing fault diagnosis[J].Journal of Ordnance Engineering College，2005，17（4）：37-40.

[7]向玲，朱永利，唐贵基.HHT方法在转子振动故障诊断中的应用[J].中国电机工程学报，2007，27（35）：84-88.

[8]Huang N E，Shen Z，Long S R.A New View of Nonlinear Waves：The Hilbert Spectrum [J].Annual Review Fluid Mechanics，1999，31（5）：417-457.

[9]何正嘉.机械设备非平稳信号的故障诊断原理及应用[M].北京：高等教育出版社，2001.

[10]Huang N，Shen Z，Long S.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceeding of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences，1998，454：903-995.

[11]Cheng Junsheng，Yu Dejie，Tang Jiashi.Rubimpact fault diagnosis of the rotor systems based on EMD[J].Mechanism and Machine Theory，2009，44：784-791.

[12]Zhike P，Peter W T，Fulei Chu.An improved Hilbert-Huang transform and its application in vibration signal analysis[J].Journal of Sound and Vibration，2005，286：187-205.