高中数学竞赛训练题

高中数学竞赛训练题

一、填空题

2.方程9x+|1-3x|=5的实数解为______．

3.方程||…|||x|-1|-2|…|-2 013|=2 013一共有______个解.

4.若平面向量a,b满足|2a-b|≤3，则a·b的最小值是______．

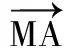
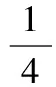
(第3届澳门高中数学奥林匹克竞赛试题)

7．已知集合A={a1,a2,a3}⊆{1,2,3,…,2 013}，且a1+10≤a2+1≤a3，则满足条件的集合A有______个.

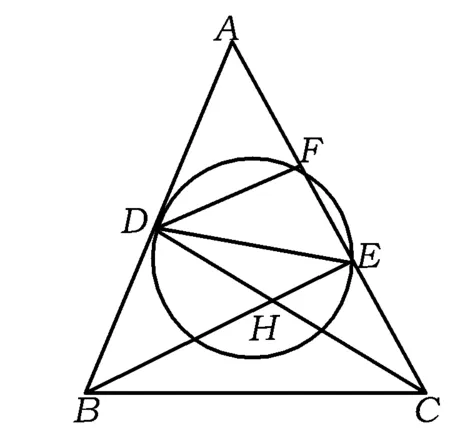
图1

8．如图1，已知在锐角△ABC中，BE⊥AC于点E，CD⊥AB于点D，BC=25，CE=7，BD=15，以DE为直径的圆与AC交于点F，则AF=______．

(2012年华约自主招生试题)

9.在1,2，…,2 012中取一组数，使得任意2个数之和不能被其差整除，最多能取______个数.

(2012年北约自主招生试题)

二、解答题

(2009年全国高中数学联赛安徽省预赛试题)

12．试构造函数f(x)，g(x),使其定义域为(0,1)，值域为[0,1]，且

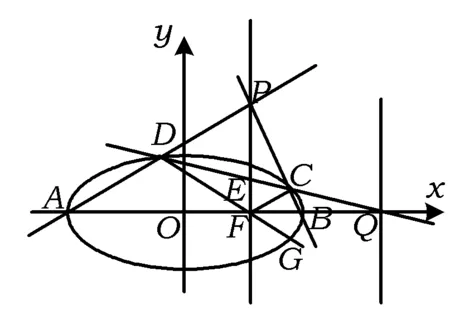
图2

(1)对于任意a∈[0,1]，f(x)=a只有1个解；

(2)对于任意a∈[0,1]，g(x)=a有无穷多个解．

(2006年复旦大学自主招生试题)

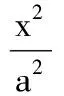
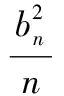
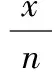
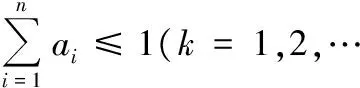
18．设平面上有3个点，任意2个点之间距离不超过1，问：半径至少为多大的圆盘才能覆盖这3个点？请证明你的结论．

19．已知函数f(x)=ex-x，其中e为无理数(e=2.718 28…).

(1)若函数F(x)=f(x)-ax2-1的导函数F′(x)在[0,+∞)上是增函数，试求实数a的最大值；

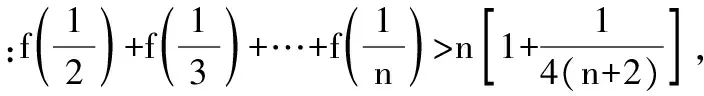
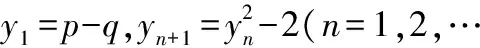
21．已知四面体ABCD的3对对棱分别相等.

(1)证明：4个面都是锐角三角形．

(2)设△ABC，△ABD，△ACD所在平面与△BCD所在平面所成的角分别为α，β，γ,求证：cosα+cosβ+cosγ=1．

(2009年清华大学自主招生试题)

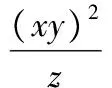
23．试确定，是否存在2 011个实数a1,a2,…,a2 011，满足：

(1)|ai|<1(i=1,2,…,2 011)；

(2)|a1|+|a2|+…+|a2 011|-|a1+a2+…+a2 011|=2 010．

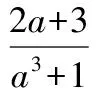
参考答案

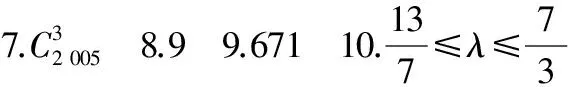
11.解由方程可知x是整数,设x=42p+q，其中p∈Z，q∈{0,1,…,41},则

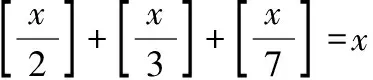
因此,方程的解集为

则f(x)满足题意．

13.解记椭圆的右焦点为F，联结CF,DF,PF，其中DF交椭圆于点G，PF交DQ于点E．根据椭圆第二定义，知

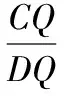
FQ为△DFC中∠DFC的外角平分线，则

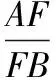
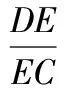
由式(1),得

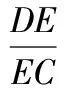
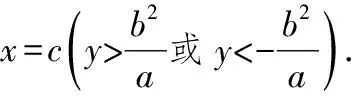
图3

14.解如图3，以右焦点F为极点、x轴正半轴为极轴建立极坐标系，则椭圆的极坐标方程为

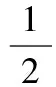
|MM1|=2ρ1,|NN1|=2ρ2,

则

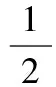
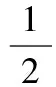
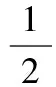
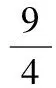
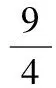
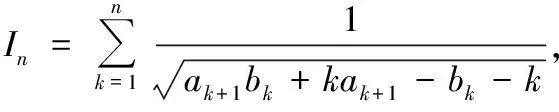
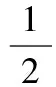
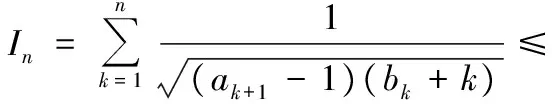
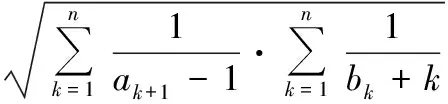
因为a1=1，an+1=an+2n,所以ak+1-1=k(k+1),从而

(3)

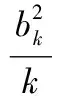
即

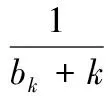
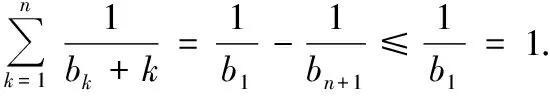
(4)

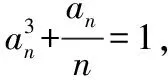
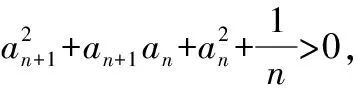
an+1-an>0，

即

an+1>an.

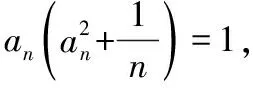
从而

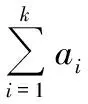
令bk=ak-ak+1，则对任何k，bk≥0且根据ak-2ak+1+ak+2≥0有bk≥bk+1,于是

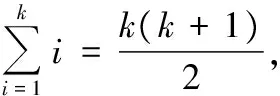
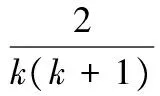
即

…

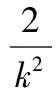
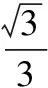
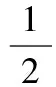
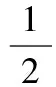
累加,得

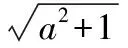
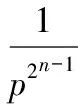
从而

由数学归纳法，得

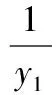
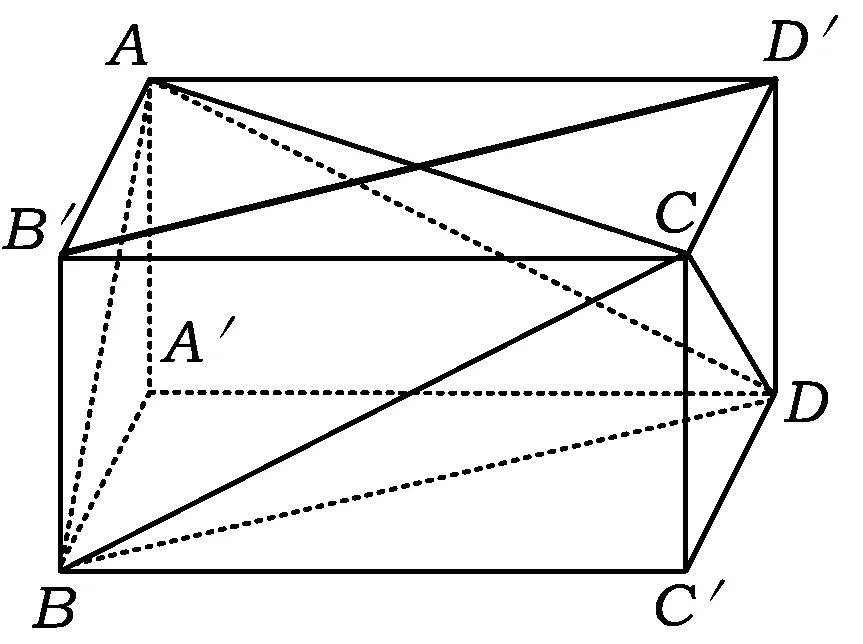
图4

21.证明(1)过四面体的每一条棱都存在着与对棱对棱平行的平面，这6个平面的交线围成了一个平行六面体AB′CD′-A′BC′D(如图4所示),联结B′D′.因为

BD=B′D′，BD=AC,

所以

AC=B′D′,

从而四边形AB′CD′是对角线相等的平行四边形，即四边形AB′CD′是矩形．同理另外的5个面也都是矩形，故该平行六面体为长方体，四面体ABCD的棱均为该长方体的面对角线．

现设AB′=a，B′C=b，B′B=c，则

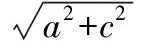
即∠BAC是锐角.同理可证∠ABC与∠ACB也都是锐角,于是△ABC是锐角三角形.同理可证另外3个三角形也都是锐角三角形，因此，四面体ABCD的4个面都是锐角三角形．

(2)如图5所示，设四面体ABCD的顶点A在平面BCD上的射影为A′，联结BA′，CA′，DA′，则

S△A′BC+S△A′CD+S△A′BD=S△BCD,

从而

图5

因为四面体ABCD是3对对棱分别相等的四面体,所以它的4个三角形全等,于是

S△ABC=S△ACD=S△ABD=S△BCD,

故 cosα+cosβ+cosγ=

22.证明因为x+y+z=(x+y+z)(xy+yz+zx)=xy(x+y)+yz(y+z)+xz(x+z)+3xyz，所以原题即证

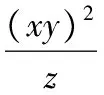
xy(x+y)+yz(y+z)+xz(x+z).

(5)

根据对称性，不妨设x≥y≥z，则

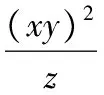
(6)

同理可得

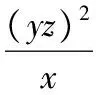
(7)

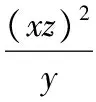
(8)

注意到

又由x≥y≥z,知

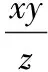
式(6)+式(7)+式(8),得

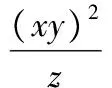
yz(y+z)-zx(z+x)≥0，

即式(5)成立，当且仅当x=y=z时等号成立．从而所证结论成立．

23.证明假若存在满足以上条件的2 011个实数a1,a2,…,a2 011，设|a1+a2+…+a2 011|=t，则t≥0，去掉绝对值符号，并分开其正、负部，可记为

|a1+a2+…+a2 011|=

(x1+x2+…+xk)-(y1+y2+…+y2 011-k)，

即 (x1+x2+…+xk)-(y1+y2+…+y2 011-k)=t,

(9)

其中x1,x2,…,xk；y1,y2,…，y2 011-k是|a1|,|a2|,…,|a2 011|的某个排列．由条件(2)，知

(x1+x2+…+xk)+ (y1+y2+…+y2 011-k)=2 010+t,

(10)

从而

x1+x2+…+xk=1 005+t,

y1+y2+…+y2 011-k=1 005.

(11)

由于0≤xi≤1，0≤yj<1(i=1,2,…,k；j=1,2,…,2 011-k),则

k>x1+x2+…+xk=1 005+t;

即

2 011-k>y1+y2+…+y2 011-k=1 005,

于是

k≥1 006，2 011-k≥1 006,

相加得2 011≥2 012，矛盾．

因此，这样的2 011个实数不存在．

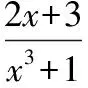
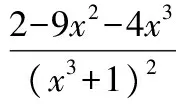
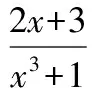
即

因为

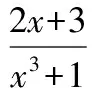
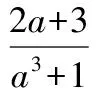
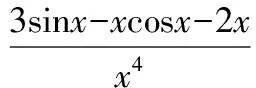
记g(x)=3sinx-xcosx-2x，则

g′(x)=2cosx+xsinx-2.

因为

g″(x)=xcosx-sinx=cosx(x-tanx)，

g‴(x)=-xsinx<0，

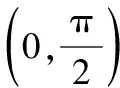
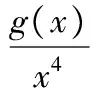
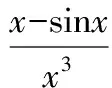
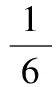
(供稿：睿达资优教育命题组)