活跃在竞赛中的含绝对值不等式问题

●

(杭州市第十一中学 浙江杭州 310014)

活跃在竞赛中的含绝对值不等式问题

●蔡小雄

(杭州市第十一中学 浙江杭州 310014)

绝对值是中学数学中一个重要的运算符号，它常与函数、方程及不等式“联袂登场”．当然，也正因为有了绝对值的加入，使得有些问题变得更加“神秘莫测”，尤其是含有绝对值的不等式问题，往往是数学竞赛参赛选手“谈虎色变”的主要内容．本文通过对一些典型试题的剖析力图揭开其神秘面纱，寻找隐藏在问题深处的规律，从而突破难点，举一反三．

1 特值探路

通过取若干个符合题设条件的特殊值寻找问题成立的特殊情形，并从特殊情形中寻找解题突破口，这是解决含绝对值问题常用的一种方法．

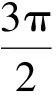
式(1)+式(2)与式(2)+式(3)可分别得到A≥0,A≤0．从而A=0，B≠0,可得

与假设矛盾．

2 和式变换

在含绝对值问题中，对于涉及2个数列对应项之积求和的问题，利用和式变换，尤其是Abel分部求和公式往往能出奇制胜．

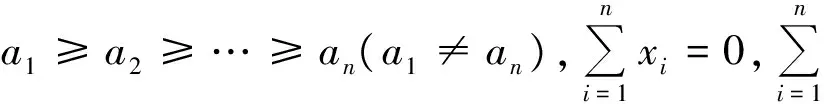
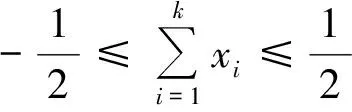
(1989年全国高中数学联赛试题)

3 正难则反

对于有些含绝对值的不等式问题，当我们直接去解决有困难时，不妨换一个角度，从其反面去思考，得出矛盾后否定假设从而证明原命题的正确性，这就是正难则反思想，体现在解题方法上就是反证法．

(第20届美国数学奥林匹克竞赛试题)

4 系数代换

将原函数或方程中的系数用给定区间的端点值或中点值代换，再通过绝对值不等式“|a|-|b|≤|a±b|≤|a|+|b|”放缩得到目标，这也是解决含绝对值不等式问题的一种较好的方法．

例4已知二次函数f(x)=ax2+bx+c在[-1,1]上的函数值的绝对值不超过1，求|a|+|b|+|c|的最大值．

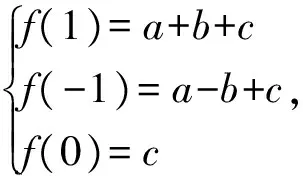
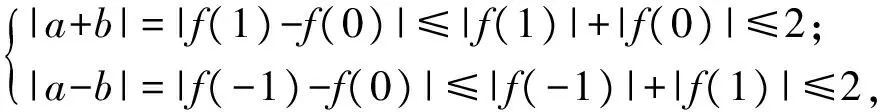
从而

|a|+|b|=max{|a+b|,|a-b|}≤2.

又|c|≤1，得|a|+|b|+|c|≤3，取a=2,b=0,c=-1可取等号，故|a|+|b|+|c|的最大值为3．

5 放缩迭代

对于有些含绝对值的数列型不等式问题，有时可利用题设条件如三角函数的有界性进行放缩，再借助放缩后的递推不等式进行迭代求得结果．

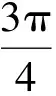
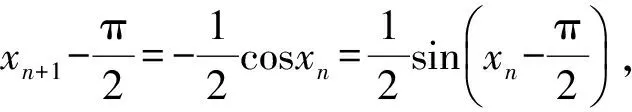
因此

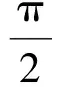
6 归纳证明

数学归纳法是解决与自然数有关问题的重要方法，对于含绝对值的不等式问题也不例外．

例6求证：|sinnx|≤n|sinx|(n∈N*).

证明用数学归纳法证明如下：

(1)当n=1时，不等式显然成立;

(2)假设当n=k时不等式成立，即|sinkx|≤k|sinx|，则当n=k+1时，有

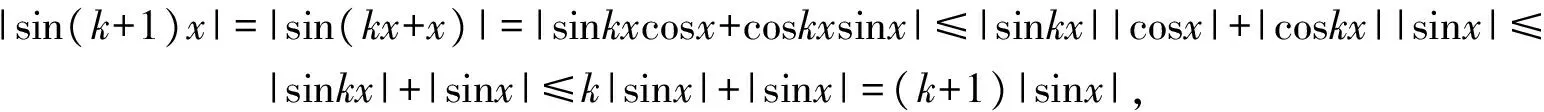
即当n=k+1时，不等式也成立.由(1)，(2)可知|sinnx|≤n|sinx|(n∈N*)成立．

7 分类讨论

分类讨论是去绝对值的一种有效方法，即使是对于多绝对值的问题，适当地进行分类讨论也能简化计算，化解难点．

例7设x,y∈R，M=max{|x+y|,|x-y|,|1-x|,|1-y|},试求M的最小值．

解(1)当xy≥0时，|x-y|≤|x|+|y|=|x+y|，因此

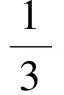
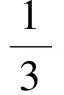
(2)当xy<0时，max{|1-x|,|1-y|}>1，因此

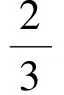
8 复数客串

复数的模与实数中的绝对值是一对“孪生兄弟”，根据题目条件化“实”为“虚”，有时也能使原问题的解决柳暗花明．

证明设z1=ax+byi，z2=bx+ayi,则

|z1|+|z2|≥|z1+z2|=|x(a+b)+y(a+b)i|=|a+b||x+yi|=|a+b|.

9 构造向量

与复数的模类似，向量的模与绝对值也有非常密切的联系，因此，不妨通过构造向量，充分运用这种联系来解题．