数列不等式的求解策略

●

(南京市外国语学校 江苏南京 210008)

数列不等式的求解策略

●黄志军

(南京市外国语学校 江苏南京 210008)

数列和不等式证明是紧密相连、互相渗透的，将数列与不等式结合起来构成的数列不等式,既具有数列的结构与性质特征,又具有不等式证明的思想方法.因其涉及面广、综合性强、难度较大,因而在高中数学竞赛及高校自主招生试题中屡见不鲜.

数列不等式是在数列的特殊情景下,巧妙地融合了不等式证明的思想方法,它所涉及的问题往往灵活应用了数列和不等式的知识,我们一定要注意它们的联系,在知识的交叉点上思考分析,合理运用数列的性质,尤其是合理使用不等式的放缩方法.下面给出解决数列不等式问题的几种常用策略,供参考.

1 裂项相消法放缩

证明由题设条件和结论,可设d=ai-ai-1>0,则

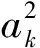
故

当且仅当d=0时，等号成立.

评析当运用拆(裂)项放缩时，需根据题型结构，认真分析不等式的特征，把握放缩的幅度，构造相应的拆(裂)项模式，并不断调整和完善，从而准确选择解题思路.

2 运用基本不等式性质放缩

(1)证明:an+1>an;

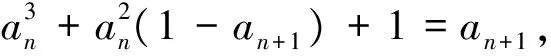
从而

即

an+1>an.

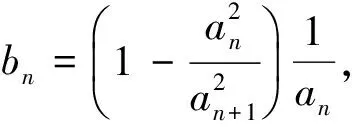
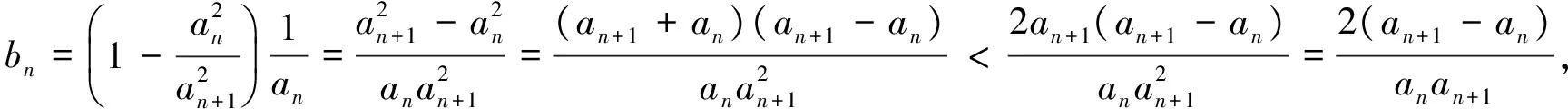
所以

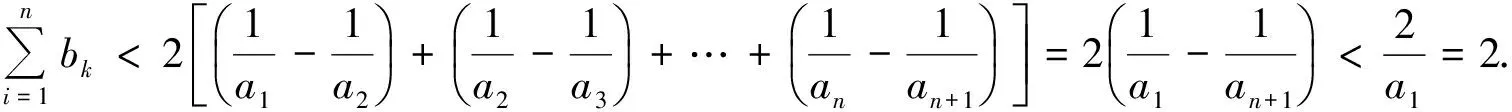
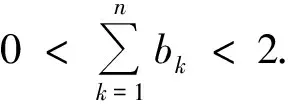
评析利用基本不等式的性质进行放缩，需要在递推关系的变形中寻找用得上的不等关系，抓住表达式的结构特征是恰当运用基本不等式性质进行递推放缩的关键.

3 构造函数，利用函数性质放缩

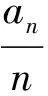
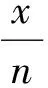
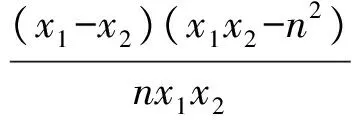
可知函数f(x)是区间(0，n]上的减函数．

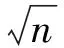
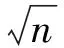
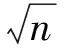
即

故对一切n∈N*，n≥3，均有

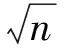
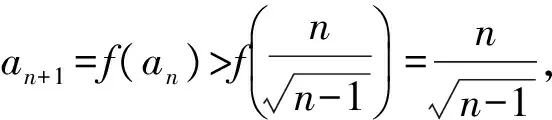
等价于

2n2(n-3)+4n-1>0，

评析数列是一类特殊的函数，利用函数的单调性研究数列的单调性，是证明数列不等式的重要方法之一.在构造函数时，应抓住数式中项的递变规律，联想相应的函数表达式，恰当构造.

4 构造数列，综合运用放缩法.

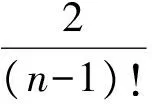
(2)求正整数a,b,c，使得对任意n∈N*(n>2)，有

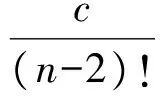
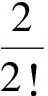
即

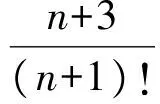
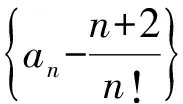
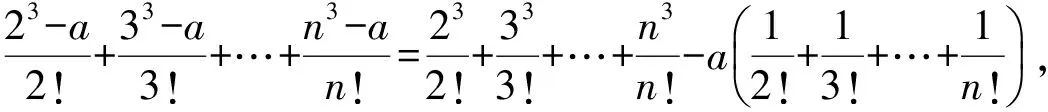
通过不完全归纳计算：当a=5，b=9时，有

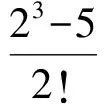
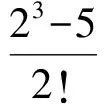
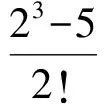
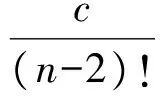
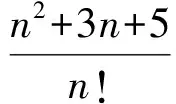
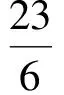
n2+3n+5<4n(n-1),

亦即

3n2-7n-5>0⟺3n(n-3)+2(n-3)+1>0,

评析构造数列也是证明数列不等式的重要方法之一，尤其在证a1+a2+…+an≥f(n)型不等式时，可将f(n)视为{bn}的前n项和，则只需证an≥bn，这样目标明确，推理容易进行.

5 综合运用数学思想放缩

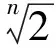
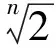
(1)

由贝努利不等式，得

结合式(1)，式(2)可得

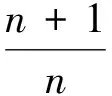
下面用数学归纳法证明：

其中n是非负整数.

当n=0时,式(4)左边为aM，右边也为aM,故式(4)成立.

当n=k(k∈N+∪{0})时，式(4)成立，即

在式(3)中取n=M+k+1，并利用式(5)，可得

故式(4)在n=k+1时也成立，得证.

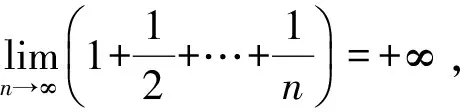
即

故存在正整数N0，满足

在式(4)中取n=N0-M-1，得

结合式(6)，式(7)知aN0-1<0，这与aN0-1>0矛盾，从而命题得证.

评析数列不等式的证法千变万化,要解决好此类问题需具备扎实的数学功底,在通晓其基本方法的同时,还要注意总结感悟,逐步形成自身的解题思路和能力,进而感受数学之美.