平面几何中线段“和差倍分”问题的证明

●

(秀州中学分校 浙江嘉兴 314000)

平面几何中线段“和差倍分”问题的证明

●倪建荣

(秀州中学分校 浙江嘉兴 314000)

线段“和差倍分”问题是几何证明的重要内容之一，这类问题的证明方法灵活多变、技巧性强，且没有固定的解题模式，在各级各类数学竞赛中出现的频率较高．解决线段“和差倍分”问题的基本原则是转化，即通过对原问题中相关线段的变形，实现矛盾的转移，从而达到化未知为已知、化难为易、化繁为简的目的.本文拟对这类问题的常用解法作一些探讨．

1 合理割补,水到渠成

割补法(截长补短法)是证明线段“和差倍分”问题的一种重要方法，它通过“分割”或“添补”，在相关线段或其延长线上构造能够表示线段“和差倍分”的新线段，从而将多线段问题转化为2条线段问题，促使原问题的解决．

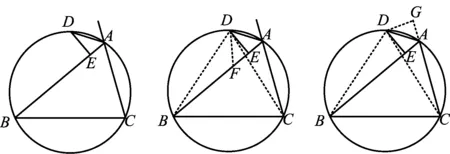
图1图2图3

证法1如图2，在BE上截取EF=AE，联结DC，DB，DF.易知DE垂直平分线段AF,则DF=DA.又由∠DFA=∠DAF=∠DAG，得∠DFB=∠DAC.而∠DBF=∠DCA，从而△DBF≌△DCA，得BF=AC，即AB-AC=2AE.

证法2如图3，延长CA至点G，使AG=AE，联结DC,DB,DG.易证△ADE≌△ADG，从而可证△BDE≌△CDG,得BE=CG，即AB-AC=2AE.

评注证法1在较长线段上截取，证明剩余部分相等；证法2则相反，将较短线段延伸再证明相等．证法1与证法2正好是“割”与“补”的2种方法.

例2在锐角△ABC中，∠ACB=60°，O为△ABC外接圆的圆心，H为垂心，OH的延长线交AC于点P，其反向延长线交BC于点Q.求证：AP+BQ=PQ.

证明如图4，延长BO交⊙O于点G，联结CG,AG,CH,AH.可证四边形AHCG为平行四边形，得AG=CH.由∠ACB=60°及BG为直径，得AG=CO,从而CH=CO.延长CH交⊙O于点E，联结CO并延长交⊙O于点F，联结EF，则EF∥AB，从而证得△CPH≌△CQO，因此△CPQ为等边三角形.再证明AP=PH，同理可得HQ=QB，于是AP+BQ=PQ.

评注本例巧妙地运用了圆的性质，通过构建平行四边形和全等三角形，将2条不共线的线段长度之和转化为一条线段的长度．

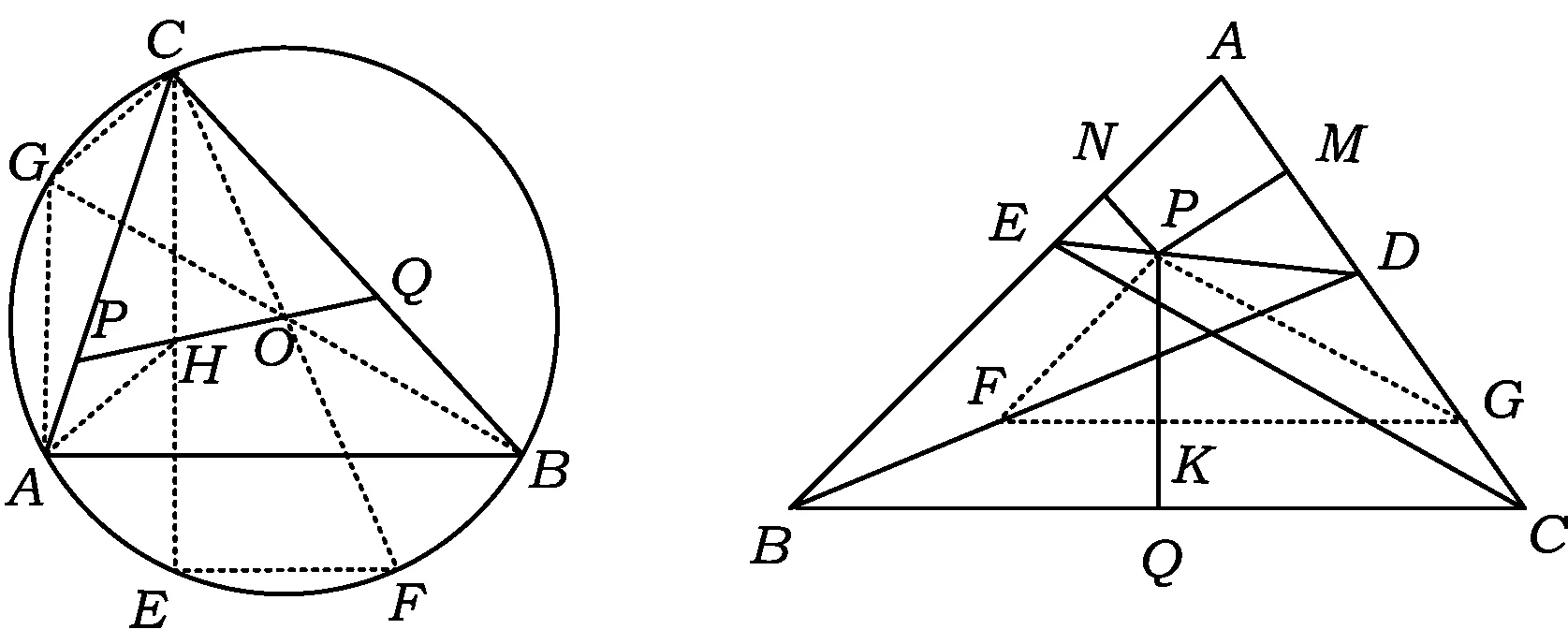
图4 图5

2 构建平行,迎刃而解

利用“平行线间距离相等”、“夹在平行线间的平行线段相等”等定理，可通过添加平行线,将某些线段“送”到恰当位置，从而获得证题思路．

例3在△ABC中,BD,CE为角平分线,P为ED上任意一点．过点P分别作AC,AB,BC的垂线,点M,N,Q为垂足．求证：PM+PN=PQ．

证明如图5，过点P作AB的平行线交BD于点F,过点F作BC的平行线分别交PQ,AC于点K,G,联结PG．由BD平分∠ABC,知点F到AB，BC的距离相等，从而KQ=PN．

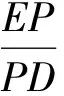
PM+PN=PK+KQ=PQ．

评注本例通过添加平行线,将PQ“掐开”成2段,证得PM=PK，于是PM+PN=PQ，体现了传递的思想，证法非常简捷．

证明如图6，过点B作AC的平行线交ND的延长线于点E．联结ME，则△BED≌△CND，从而BE=NC．又因为MD为EN的中垂线，所以EM=MN．由

BM2+BE2=BM2+NC2=DN2+MD2=MN2=EM2,

知△BEM为直角三角形,即∠MBE=90°，从而

∠ABC+∠ACB=∠ABC+∠EBC=90°,

于是∠BAC=90°．故

评注本例通过添加AC的平行线,将BC“以D为中点”的性质传递给EN，为解题找到思路．

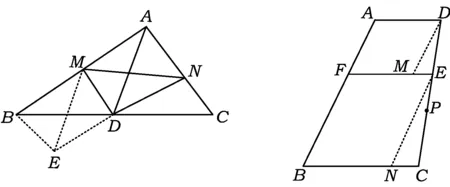
图6 图7

3 运用比例,巧妙腾挪

探寻与所求证结论有关的比例式，通过对比例式变形或重新组合，从而得出线段之间的“和差倍分”关系．

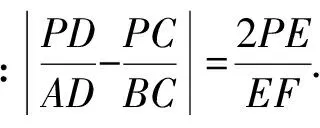
证明如图7，过点D,E分别作DM∥AB，EN∥AB，点M,N分别在EF和BC上，得平行四边形ADMF和平行四边形BFEN，从而

EM=EF-AD，CN=BC-EF，

DM=AF=AD，EN=BF=BC．

因为△DME∽△ENC，所以

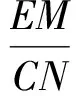
即

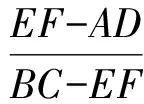
从而

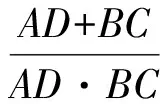
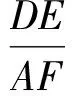
当点P在CE上时，

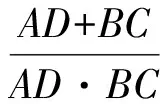
同理可知当点P在DE上时，

故

评注通过添加平行线构建三角形相似,从而产生比例线段,再结合平行线分线段成比例，巧妙腾挪,问题迎刃而解..

例6设M,N为△ABC边BC上的2个点，且满足BM=MN=NC．一平行于AC的直线分别交AB,AM,AN于点D，E，F，求证：EF=3DE．

证明如图8，过点N,M分别作AC的平行线交AB于点H,G，NH交AM于点K，从而BG=GH=HA，于是

因此

HK∶KN=1∶3.

又因为DF∥HN，所以

DE∶EF=HK∶KN=1∶3，

从而

EF=3DE．

评注由于“平行于三角形一边的直线截其他2边所得对应线段成比例”,在一些问题中,可以通过添加平行线,实现某些线段比的良性转化，这在平面几何证题中经常遇到．

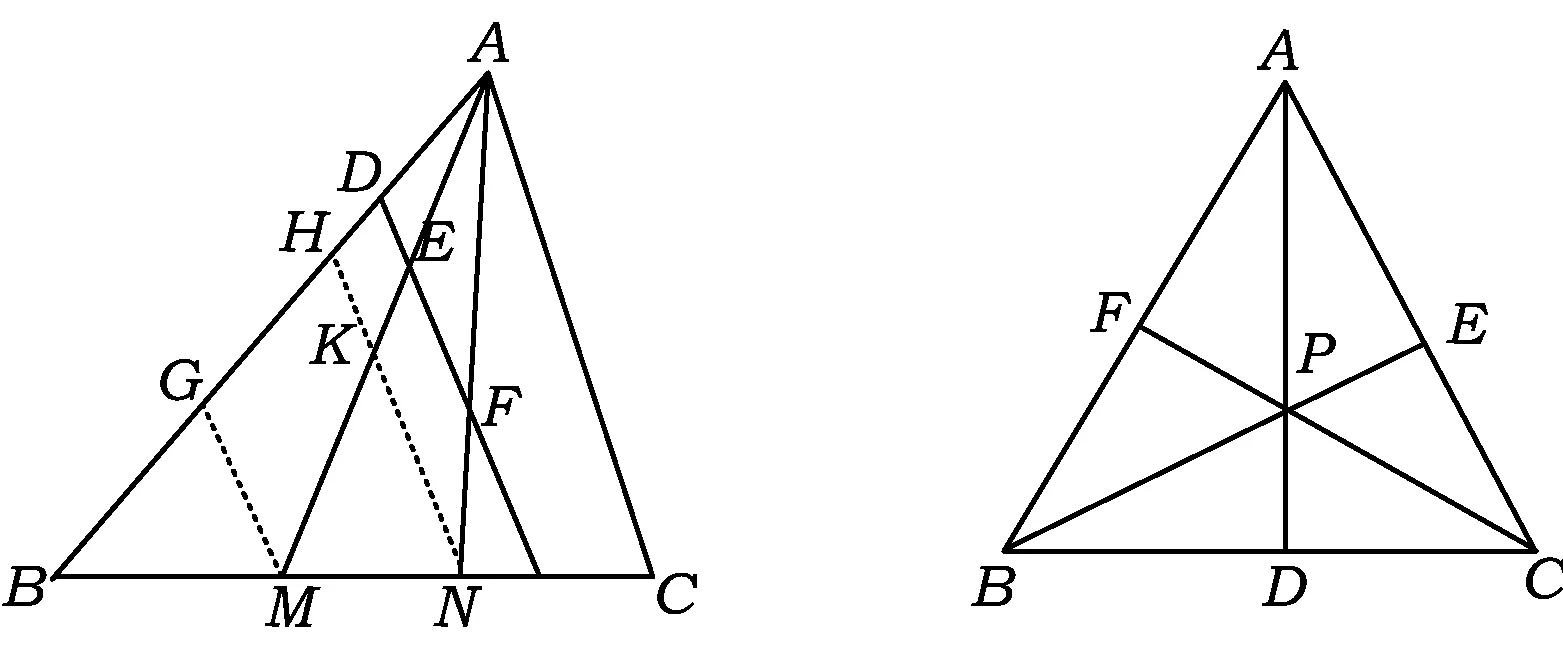
图8 图9

4 转化面积，豁然开朗

根据有关线段与图形面积之间的关系，把证明线段的比例关系转化为证明面积的比例关系，然后通过面积求算，从而得证．

例7如图9，设P是△ABC内一点，AP,BP,CP与对边分别交于点D,E,F．求证：

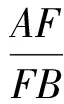
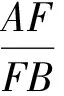
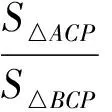
评注此结论即为塞瓦定理，用面积转化是较快的解决方法.

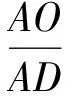
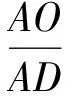
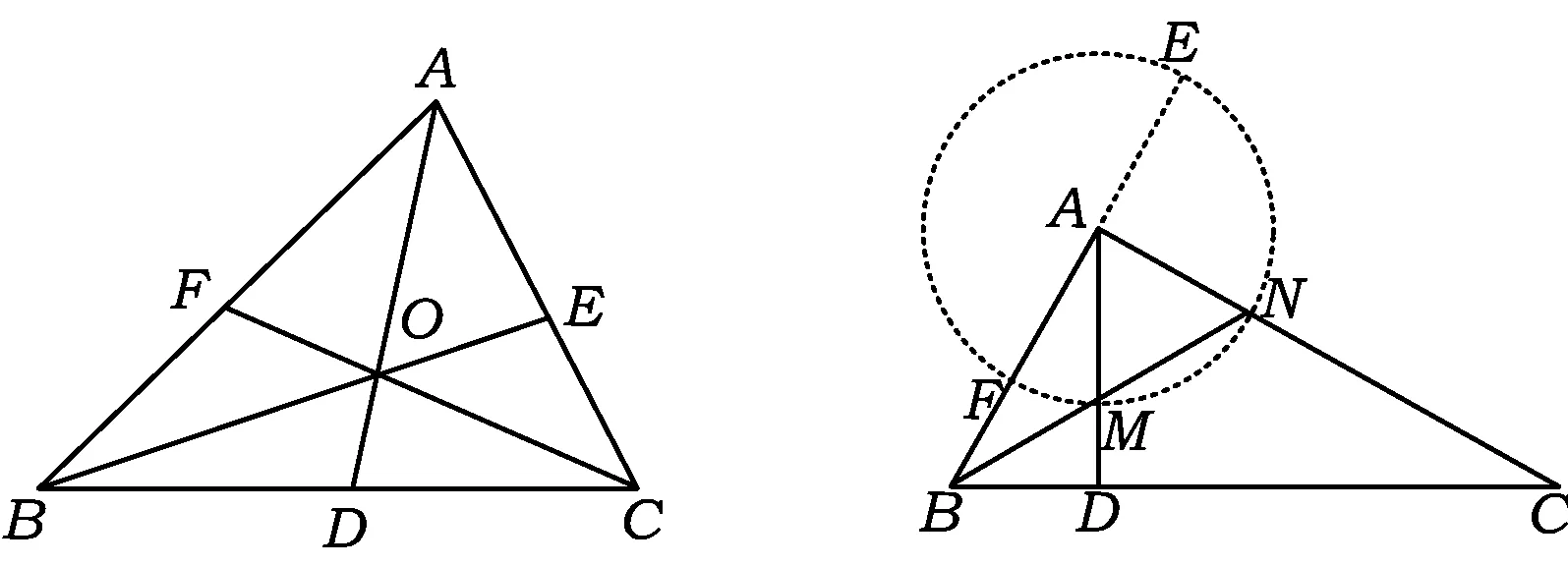
图10 图11

评注面积法是平面几何中应用十分广泛的一种重要方法．例7和例8利用线段比与面积比的相互转化，简化了证题过程．

5 构造辅圆,探囊取物

在某些数学竞赛问题中,巧妙添置辅助圆常可以沟通直线和圆的内在联系,通过圆的有关性质找到解题途径．

例9AD是Rt△ABC斜边BC上的高,∠B的平分线交AD于点M,交AC于点N．求证：

AB2-AN2=BM·BN．

证明如图11，因为

∠ANB+∠ABN=∠CBN+∠BMD=90°,

又

∠ABN=∠CBN,∠AMN=∠BMD,

所以

∠AMN=∠ANB．

从而

AM=AN．

以AM长为半径作⊙A,交AB于点F,交BA的延长线于点E，从而

AE=AF=AN．

由割线定理，得

BM·BN=BF·BE=(AB+AE)(AB-AF)=

(AB+AN)(AB-AN)=

AB2-AN2，

即AB2-AN2=BM·BN．

评注AB2-AN2=(AB+AN)(AB-AN)=BM·BN,而由题设易知AM=AN,联想割线定理,构造辅助圆即可证得结论．

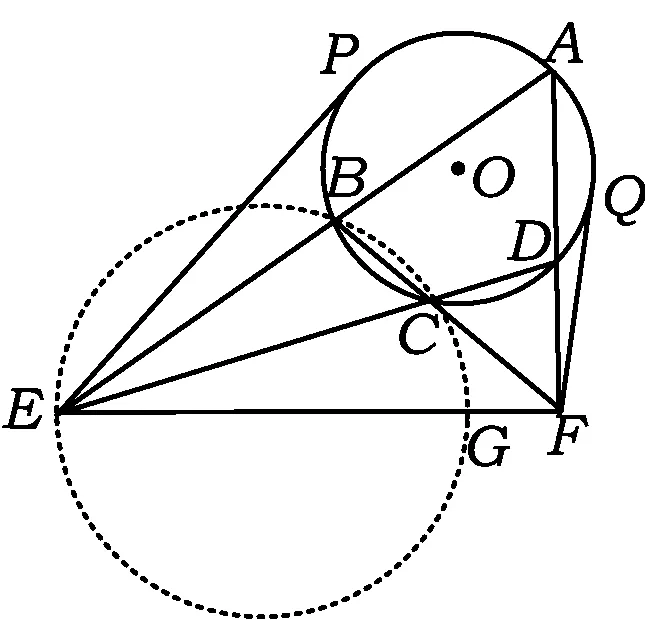
图12

例10四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点E，延长AD和BC相交于点F,EP和FQ分别切⊙O于点P,Q．求证：EP2+FQ2=EF2．

证明如图12，作△BCE的外接圆交EF于点G,联结CG．因为∠FDC=∠ABC=∠CGE,所以点F,D,C,G共圆．由切割线定理,得

EF2= (EG+GF)·EF=EG·EF+GF·EF=

EC·ED+FC·FB=EP2+FQ2,

即

EP2+FQ2=EF2．

评注通过分析问题所提供的信息,恰当补出辅助圆,并合理挖掘图形隐含的性质,从而使题设和结论的逻辑关系明朗化．