几何竞赛题求解的常见策略

●

(东阳中学 浙江东阳 322100)

几何竞赛题求解的常见策略

●陈硕罡吴国建

(东阳中学 浙江东阳 322100)

1 用函数(变量)的观点来解决问题

函数是描述客观世界中变量间依赖关系的重要数学模型.抓住问题中引起变化的主变量，并用一个具体的量(斜率或点的坐标等)来表示它，同时把问题中的的因变量用主变量表示出来，从而变成一个函数问题，这就是解决问题的函数观点.在解析几何问题中，经常会碰到由于某个量(很多时候是线或点)的变化，而引起图形中其他量(面积或长度等)变化的情况，因此函数观点成为解决解析几何问题的一种重要方法.

例1已知抛物线y2=6x上的2个动点A(x1,y1)和B(x2,y2),其中x1≠x2且x1+x2=4.线段AB的垂直平分线与x轴交于点C,求△ABC面积的最大值.

(2010年全国高中数学联赛试题)

分析通过对题目的分析可以发现,线段AB中点的横坐标已经是定值，只有纵坐标在变化，可以把AB中点的纵坐标作为主变量，这样只要把△ABC的面积表示成关于AB中点纵坐标的函数即可，这时问题就转化为求函数的最值问题.

解设线段AB中点M的坐标为(2,y0)，则直线AB的斜率为

线段AB的中垂线方程为

易知线段AB的中垂线与x轴的交点为定点C(5,0),直线AB的方程为

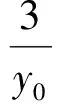
联立抛物线方程,消去x可得

由题意知，y1，y2是方程(1)的2个实根，且y1≠y2，从而

即

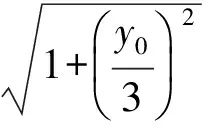
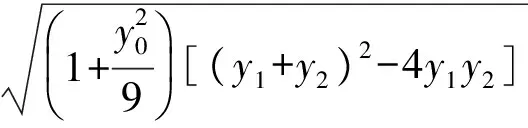
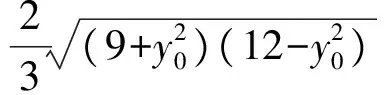
又点C(5，0)到直线AB的距离为

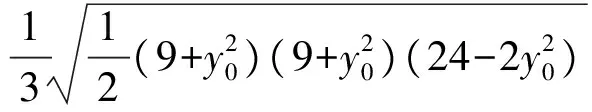
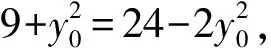
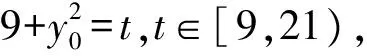
(2009年全国高中数学联赛试题)

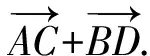
(3+4k2)x2+8kmx+4m2-48=0.

设A(x1,y1)，B(x2,y2)，则

Δ1=(8km)2-4(3+4k2)(4m2-48)>0.

(2)

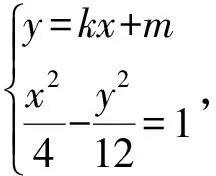
(3-k2)x2-2kmx-m2-12=0.

设C(x3,y3)，D(x4,y4)，则

Δ2=(-2km)2+4(3-k2)(m2+12)>0.

(3)

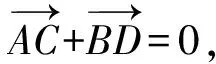
(x4-x2)+(x3-x1)=0，

此时

(y4-y2)+(y3-y1)=0.

由x1+x2=x3+x4,得

从而

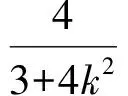
解得

k=0或m=0．

当k=0时，由式(2)和式(3)得

因为m是整数，所以m的值为-3，-2，-1，0，1，2，3．当m=0时，由式(2)和式(3)得

因为k是整数，所以k=-1，0，1．

于是满足条件的直线共有9条．

评注当题目中的主变量需要用2个变量来表示时，可先把这个因变量表示为一个二元函数，如果题设中有其他条件能找到这2个变量间的关系，那么只需用一个量来表示另一个量，这时就可转化为一元函数，这也体现了解析几何中“设而不求”的思想；如果题设条件不能直接给出2个变量者之间的关系，那么可直接对二元函数进行处理.

2 用平面几何的知识来解决问题

解析几何是用坐标法把几何问题代数化，用代数的方法解决几何问题，但说到底解析几何还是几何.在解决某些解析几何问题时，若其平面几何背景非常明显，则可以借助平面几何知识快速、准确地解决问题.

(2012年全国高中数学联赛试题)

解由抛物线的定义及梯形的中位线定理得

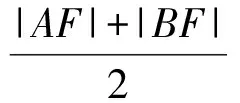
在△AFB中,由余弦定理得

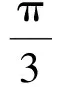
(|AF|+|BF)2-3|AF|·|BF|≥

评注一些解析几何客观题，往往需要借助圆锥曲线的定义和平面几何的一些性质进行解题.

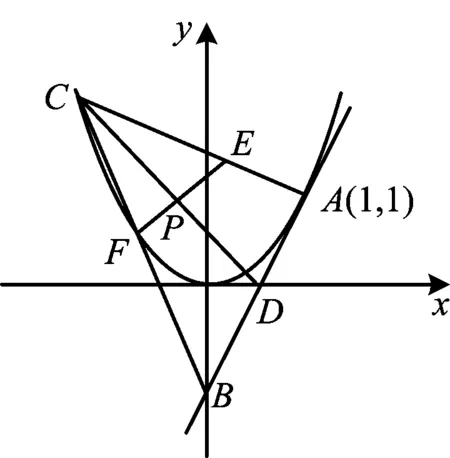
图1

(2005年全国高中数学联赛试题)

分析通过粗略计算可知点D为AB的中点，而题设中有很多线段比例关系，因此可考虑用三角形的面积之比来解决问题.

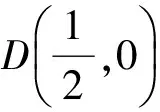
S△CAB=2S△CAD=2S△CBD,

得

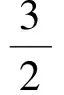
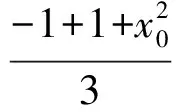
消去x0得

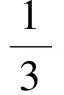
因此所求的轨迹方程为

评注从函数的观点进行分析，易发现点C的横坐标x0为主变量，点P的横坐标和纵坐标均可表示成关于x0的函数，再消去参数x0就得到点P的轨迹方程.思路虽然简单，但由于本题所含字母较多，进行代数运算时运算量大且容易出错.如果能够分析其平面几何背景，运用平面几何的知识，就能比较快速、准确地解决问题.

3 用极坐标知识来解决解析几何问题

解析几何中的坐标法是指建立直角坐标系，用点在2个坐标轴上的射影来确定.而极坐标是用角度和距离(长度)这2个量来确定一个点的位置，其几何意义很明显.如果在题目中涉及到的量能用角度和距离非常方便地表示出来，那么建立一个极坐标系进行运算，会比我们在直角坐标系下运算快速有效得多.

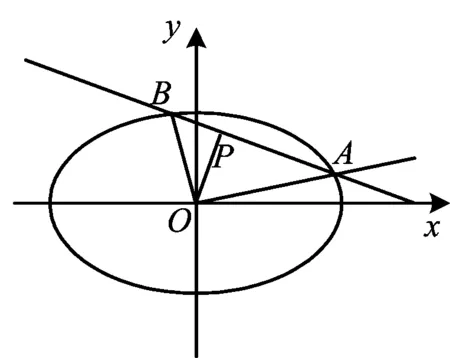
图2

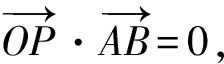
(2008年江苏省高中数学竞赛试题)

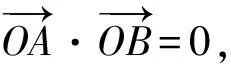
解(1)如图2，以原点为极点、x轴正半轴为极轴建立极坐标系.设|OA|=a，|OB|=b,∠AOx=θ，则

A(acosθ，asinθ)，

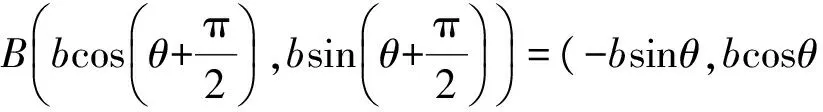
点A,B在椭圆上，得

即

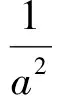
同理可得

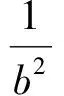
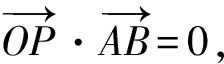
|OP|·|AB|=|OA|·|OB|，

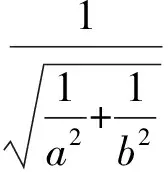
图3

例6在平面直角坐标系xOy中，菱形ABCD的边长为4，且|OB|=|OD|=6．

(1)求证：|OA|·|OC|为定值；

(2)当点A在半圆(x-2)2+y2=4(2≤x≤4)上运动时，求点C的轨迹．

(2012年全国高中数学联赛试题)

分析如图3，根据菱形和等腰三角形的性质可知点O,A,C共线，结合菱形的对角线垂直可知边长关系，第(1)小题用平面几何方法可快速求解.由点O,A,C共线知3个点的角度是一样的，只

有长度不一样，加上第(1)小题的结论可知，|AO|与|OC|的长度之积为定值20，第(1)小题可以用极坐标(ρ,θ)求解.

解(1)因为|OB|=|OD|,|AB|=|AD|=|BC|=|CD|,所以点O,A,C共线.如图3,联结BD,则BD垂直平分线段AC,设垂足为K,于是

|OA|· |OC|=(|OK|-|AK|)·(|OK|+|AK|)=

|OK|2-|AK|2=

(|OB|2-|BK|2)-(|AB|2-|BK|2)=

|OB|2-|AB|2=62-42=20(定值).

而点A所在的半圆的极坐标方程为

可得ρ1=4cosθ，代入式(4)可得

再转化为直角坐标

x=ρ2cosθ=5,y=ρ2sinθ=5tanθ∈[-5,5],

故点C的轨迹为线段x=5(-5≤y≤5).

高中数学竞赛中解析几何题的解题策略多种多样，比如用直线的参数方程来求解有关定点到动点距离的问题比较方便，用曲线的参数方程在化两元为一元的问题上有很多的优势等.只有掌握一些常用的技巧和方法，在做题的时候根据题设、结论的背景和特征，选择合适的方法，才能快速、准确地解决解析几何问题.